20  Apprentissage artificiel avec mlr3

Dans ce chapitre, nous explorerons plusieurs visualisations pour comparer la performance des algorithmes d’apprentissage artificiel; nous utiliserons des packages mlr3.

• Nous démontrons d’abord la pertinence des packages mlr3 pour la comparaison d’algorithmes d’apprentissage artificiel.
• Nous utilisons ensuite mlr3 pour définir et exécuter une évaluation comparative de plusieurs problèmes de classification binaire, et de plusieurs algorithmes d’apprentissage (plus proches voisins, modèles linéaires, réseaux de neurones).
• Nous générons différents graphiques de taux d’erreur et d’aire sous la courbe ROC.
• Nous ajoutons l’interactivité aux courbes ROC, pour présenter plusieurs niveaux de détail (données, itération de validation croisée, seuil des faux positifs).
• Nous visualisons les mesures de fidélité et d’erreur par rapport à l’ensemble de validation, pour confirmer que le surapprentissage et le sous-apprentissage ont été évités.

20.1 Avantages de mlr3

Plusieurs packages R proposent des algorithmes d’apprentissage artificiel, par exemple :

• library(kknn) offre des K Plus Proches Voisins (KPPV), présentés dans le chapitre 10.
• library(glmnet) offre des modèles linéaires avec régularisation L1, comme le LASSO, que nous avons explorés dans le chapitre 11.
• library(torch) offre des réseaux des neurones, exposés dans le chapitre 18.

Pour obtenir de bons résultats de prédiction sur un jeu de données, nous entraînons plusieurs algorithmes, car nous ignorons quel algorithme aura les meilleures performances pour ces données. Nous utilisons donc différents packages et analysons ensuite les résultats pour déterminer quel algorithme fournit les meilleures prédictions. Dans chaque package, les fonctions pour l’apprentissage et la prédiction ont différents noms, et différentes interfaces. En général, chaque package contient une fonction predict() qui calcule les prédictions, mais le type de sortie est différent d’un package à l’autre (factor pour classe, matrix pour probabilités de chaque classe, etc.). Comment adapter un jeux de données à chaque package d’apprentissage ? Comment uniformiser les types de sortie pour permettre la comparaison de résultats ? Le package mlr3 offre plusieurs fonctions qui simplifient ce type d’analyse, appelé « benchmark » (Bischl et al. 2024).

• Chaque jeu de données est représenté comme un Task, c’est-à-dire un tableau de données d’apprentissage accompagné de quelques métadonnées indiquant les colonnes à utiliser pour différents rôles (entrée, sortie, etc.).
• Chaque algorithme d’apprentissage est représenté comme une classe Learner qui fournit les prédictions dans un type de sortie uniforme (une matrice de probabilités pour chaque classe).

Dans ce chapitre, nous expliquons l’utilisation d’animint2 pour la visualisation interactive des résultats des différents algorithmes d’apprentissage sur différents jeux de données. Le code utilisé dans ce chapitre est une version modifiée d’un code pour la création des visualisations statiques (Hocking 2025).

20.2 Définition et exécution d’une analyse comparative

Dans mlr3, une comparaison « benchmark » comprend le calcul de toutes les combinaisons des éléments suivants :

• une liste de jeux de données (Tasks);
• une liste d’algorithmes d’apprentissage (Learners);
• toutes les itérations d’une méthode de rééchantillonnage (Resampling).

20.2.1 Jeux de données (Tasks)

Nous utilisons d’abord une liste de deux jeux de données.

mlr.tasks <- c("spam","sonar")
task_list <- mlr3::tsks(mlr.tasks)

Ensuite, nous définissons une fonction pour télécharger un jeu de données depuis le site web du livre « Elements of Statistical Learning » (Hastie, Tibshirani, et Friedman 2009).

library(data.table)
prefix <- "https://hastie.su.domains/ElemStatLearn/datasets/"
cache.fread <- function(data.name, f){
  cache.dir <- file.path("data", data.name)
  dir.create(cache.dir, showWarnings=FALSE, recursive=TRUE)
  local.path <- file.path(cache.dir, f)
  if(!file.exists(local.path)){
    u <- paste0(prefix, f)
    download.file(u, local.path)
  }
  fread(local.path)
}

Puis, nous créons une boucle pour télécharger trois jeux de données. On ajoute à chacun un Task de classification binaire (avec seulement les deux premières classes).

data.sets <- c("vowel","waveform","zip")
for(data.name in data.sets){
  suffix <- if(data.name=="zip")".gz" else ""
  set.list <- list()
  for(predefined.set in c("test","train")){
    one.set.dt <- cache.fread(
      data.name,
      paste0(data.name, ".", predefined.set, suffix)
    )
    if("row.names" %in% names(one.set.dt)){
      one.set.dt[, row.names := NULL]
    }
    setnames(one.set.dt, old=names(one.set.dt)[1], new="y")
    set.list[[predefined.set]] <- one.set.dt
  }
  task.dt <- rbindlist(set.list)[
    y %in% unique(y)[1:2] #only first two classes.
  ][, y := factor(y)]
  one.task <- mlr3::TaskClassif$new(data.name, task.dt, target='y')
  task_list[[data.name]] <- one.task
}
task_list

Le code ci-dessus produit une liste de 5 tâches de classification binaire :

• spam représente une classification de courriels (spam étant un pourriel et nonspam un courriel légitime) à partir d’un vecteur de comptage de mots « bag of words ».
• sonar représente une classification entre métal et roche, à partir d’un vecteur de bandes de fréquences sonores.
• vowel représente une classification du son des voyelles, à partir de dix variables calculées depuis un fichier audio.
• waveform est un jeu de données de simulation (Hastie, Tibshirani, et Friedman 2009).
• zip représente une classification de chiffres manuscrits, à partir d’une image de 16x16 pixels, en échelle de gris.

20.2.2 Algorithmes d’apprentissage

Dans cette section, nous définissons les algorithmes d’apprentissage à utiliser avec chaque jeu de données. Le code ci-dessous commence par une liste de deux algorithmes :

• cv_glmnet est un modèle linéaire, avec régularisation L1 qui minimise le taux d’erreur dans la validation croisée à 10 divisions (en anglais fold).
• featureless est le modèle constant, il n’utilise pas les variables d’entrée, et prédit toujours la classe la plus fréquente dans les données d’apprentissage.

learner.list <- list(
  mlr3learners::LearnerClassifCVGlmnet$new()$configure(id="cv_glmnet"),
  mlr3::LearnerClassifFeatureless$new()$configure(id="featureless"))

Nous ajoutons ensuite l’algorithme des plus proches voisins.

knn_learner <- mlr3learners::LearnerClassifKKNN$new()
knn_learner$param_set$values$k <- paradox::to_tune(1, 40)

Le code ci-dessus précise les bornes de k (le nombre de voisins) entre 1 et 40. Le code ci-dessous précise la méthode à utiliser pour la sélection de k, c’est-à-dire une recherche avec 10 valeurs, avec validation croisée à 3 divisions, qui maximise l’aire sous la courbe ROC, (en anglais Area Under the Curve  ou AUC ). Remarquons que si on veut calculer l’AUC pour l’ensemble de validation, il faut préciser predict_type="prob", ce qui fait que la prédiction est un nombre réel (et non seulement la classe la plus probable).

kfoldcv <- mlr3::rsmp("cv")
kfoldcv$param_set$values$folds <- 3
knn_learner$predict_type <- "prob"
learner.list$knn <- mlr3tuning::auto_tuner(
  learner = knn_learner,
  tuner = mlr3tuning::tnr("grid_search"),
  resampling = kfoldcv,
  measure = mlr3::msr("classif.auc", minimize = FALSE))

Ensuite, nous rajoutons deux algorithmes qui utilisent library(torch). Nous employons une fonction qui renvoie une liste d’opérateurs servant à définir les algorithmes d’apprentissage.

measure_list <- mlr3::msrs(c("classif.logloss", "classif.auc"))
n.epochs <- 200
make_po_list <- function(...)list(
  mlr3pipelines::po("scale"),
  mlr3pipelines::po(
    "select",
    selector = mlr3pipelines::selector_type(c("numeric", "integer"))),
  mlr3torch::PipeOpTorchIngressNumeric$new(),
  ...,
  mlr3pipelines::po("nn_head"),
  mlr3pipelines::po(
    "torch_loss",
    mlr3torch::t_loss("cross_entropy")),
  mlr3pipelines::po(
    "torch_optimizer",
    mlr3torch::t_opt("sgd", lr=0.1)),
  mlr3pipelines::po(
    "torch_callbacks",
    mlr3torch::t_clbk("history")),
  mlr3pipelines::po(
    "torch_model_classif",
    batch_size = 10,
    patience=n.epochs,
    measures_valid=measure_list,
    measures_train=measure_list,
    predict_type="prob",
    epochs = paradox::to_tune(upper = n.epochs, internal = TRUE)))

Remarquons que dans le code ci-dessus lr est le taux d’apprentissage. (en anglais learning rate). La fonction ci-dessous définit :

• la moitié des données d’apprentissage comme ensemble de validation (validate = 0.5), et l’autre moitié comme ensemble de sous-entraînement (pour calculer les gradients).
• que le nombre d’époques est choisi en minimisant la première mesure dans la liste measure_list (perte logistique).

make_torch_learner <- function(id,...){
  po_list <- make_po_list(...)
  graph <- Reduce(mlr3pipelines::concat_graphs, po_list)
  glearner <- mlr3::as_learner(graph)
  mlr3::set_validate(glearner, validate = 0.5)
  mlr3tuning::auto_tuner(
    learner = glearner,
    tuner = mlr3tuning::tnr("internal"),
    resampling = mlr3::rsmp("insample"),
    measure = mlr3::msr("internal_valid_score", minimize = TRUE),
    term_evals = 1, id = id, store_models = TRUE)
}

Le code ci-dessous rajoute deux algorithmes d’apprentissage.

if(torch::torch_is_installed()){
  learner.list$linear <- make_torch_learner("torch_linear")
  learner.list$dense <- make_torch_learner(
    "torch_dense_50",
    mlr3pipelines::po(
      "nn_linear",
      out_features = 50),
    mlr3pipelines::po("nn_relu_1", inplace = TRUE))
}

20.2.3 Calcul des résultats

Avant de calculer les résultats pour des algorithmes de classification, il faut préciser que predict_type=prob pour faire en sorte que les prédictions soient des valeurs réelles (et pouvoir calculer des mesures d’évaluation comme l’AUC).

for(learner.i in seq_along(learner.list)){
  learner.list[[learner.i]]$predict_type <- "prob"
}

Puis nous combinons les jeux de données, les algorithmes d’apprentissage et la méthode d’échantillonnage (validation croisée à 3 divisions).

bench.grid <- mlr3::benchmark_grid(
  task_list,
  learner.list,
  kfoldcv)

Puisque notre but est d’expliquer la visualisation, nous avons déjà calculé et sauvegardé les résultats dans library(animint2data). Le code ci-dessous télécharge ces résultats.

if(TRUE){
  if(!requireNamespace("animint2data"))
    remotes::install_github("animint/animint2data")
  data(bench.result, package="animint2data")
}else{ # to re-run execute the two lines below:
  if(require(future))plan("multisession")
  bench.result <- mlr3::benchmark(bench.grid, store_models = TRUE)
}

Loading required namespace: animint2data

Si vous souhaitez refaire le calcul pour obtenir ces résultats, exécutez la ligne benchmark() ci-dessus. L’exécution pourrait durer plusieurs minutes voire plusieurs heures, selon votre ordinateur. Le code plan("multisession") implique que chaque combinaison (données, algorithmes, divisions) est traitée par un processeur différent. Pour accélérer le processus, vous pouvez utiliser une grappe de calcul (Hocking 2025).

20.3 Graphiques d’erreur et d’aire sous la courbe

Tout d’abord, nous définissons les mesures à calculer pour évaluer les prédictions.

test_measure_list <- mlr3::msrs(c(
  'classif.auc','classif.ce','classif.tpr','classif.fpr'))
sapply(test_measure_list, function(M)M$label)

               classif.auc                 classif.ce 
"Area Under the ROC Curve"     "Classification Error" 
               classif.tpr                classif.fpr 
      "True Positive Rate"      "False Positive Rate" 

La sortie ci-dessous affiche la correspondance entre le nom et le code des mesures.

• classif.auc est l’aire sous la courbe ROC.
• classif.ce est le taux d’erreur de classification, soit le nombre d’étiquettes avec prédictions incorrectes, divisé par le nombre total d’étiquettes.
• classif.tpr est le taux de vrais positifs, soit le nombre d’étiquettes positives avec prédictions correctes, divisé par le nombre d’étiquettes positives.
• classif.fpr est le taux de faux positifs, soit le nombre d’étiquettes négatives avec prédictions incorrectes, divisé par le nombre d’étiquettes négatives.

Ensuite, nous utilisons $score() pour calculer ces mesures pour les données test, dans chaque division de validation croisée.

score_dt <- bench.result$score(test_measure_list)
score_dt[, .(task_id, learner_id, iteration, classif.auc, classif.ce)]

    task_id         learner_id iteration classif.auc classif.ce
 1:    spam classif.kknn.tuned         1   0.9639355 0.08930900
 2:    spam classif.kknn.tuned         2   0.9699876 0.08604954
---                                                            
74:     zip        featureless         2   0.5000000 0.51268116
75:     zip        featureless         3   0.5000000 0.49546279

La sortie ci-dessus contient une ligne pour chaque combinaison de données, algorithme, division de validation croisée. Il y a des colonnes pour deux mesures : l’AUC et le taux d’erreur. Le code ci-dessous visualise les taux d’erreur. Remarquons que nous convertissons le taux d’erreur en pourcentage afin d’économiser l’espace sur l’axe X (par exemple, 0.3 devient 30).

library(animint2)
score_dt[, let(percent_error=100*classif.ce)]
ggplot()+
  facet_grid(task_id ~ .)+
  geom_point(aes(
    percent_error, learner_id),
    data=score_dt)+
  scale_x_continuous(
    breaks=seq(0,100,by=10),
    limits=c(0,60))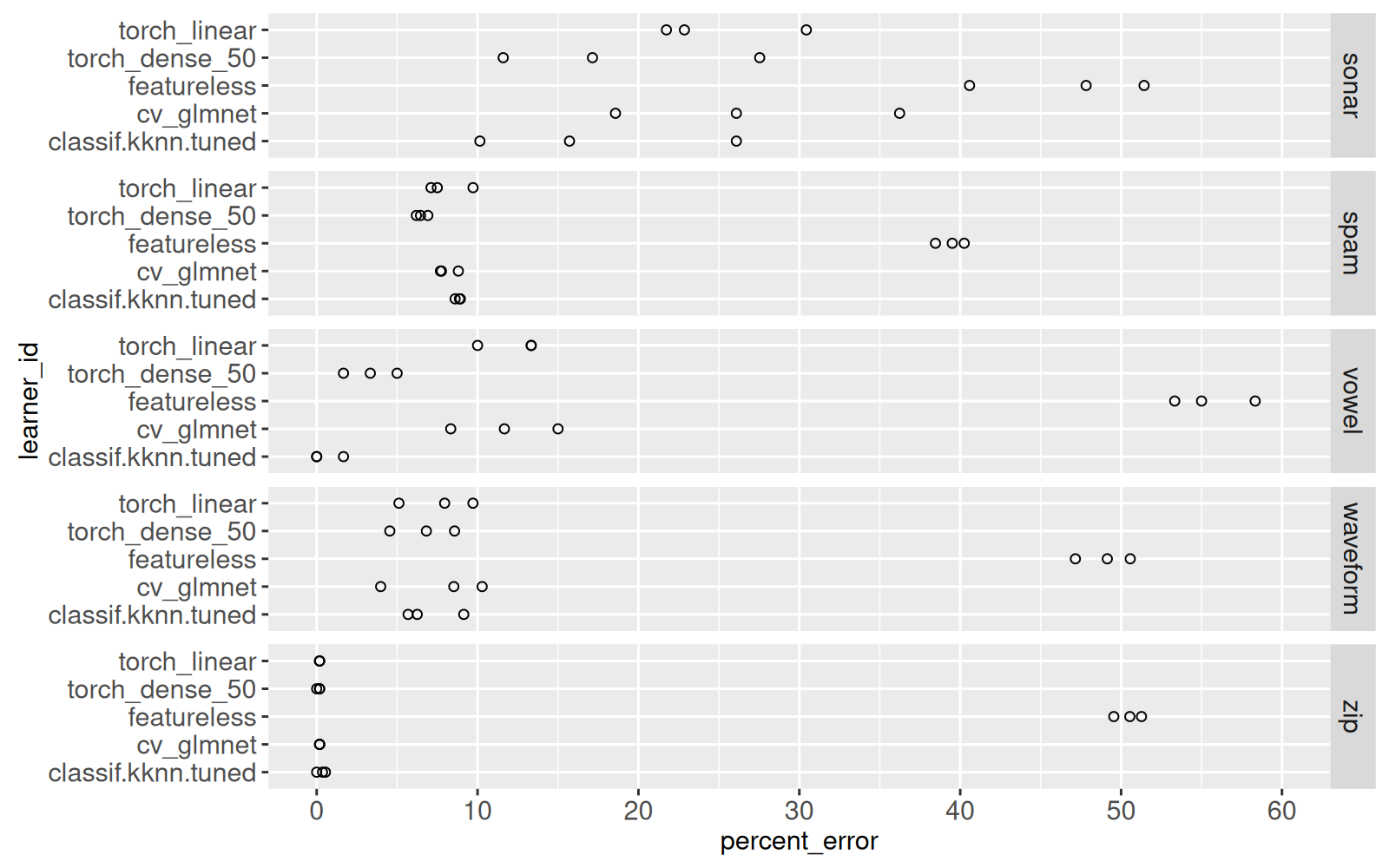

Le graphique ci-dessus affiche trois cercles pour chaque Y — un cercle pour chaque division de validation croisée. Nous voyons que l’algorithme des plus proches voisins a le plus petit taux d’erreur dans certains jeux de données (vowel), tandis que le réseau de neurones (torch_dense_50) est meilleur dans d’autres données (spam). L’objectif de ce chapitre est d’ajouter l’interactivité à ce graphique, afin de montrer les détails de chaque division de validation croisée.

20.3.1 Courbes ROC

Dans cette section, nous affichons des courbes ROC, utiles à l’évaluation en classification binaire. En fait, $score() a déjà calculé l’aire sous la courbe (AUC), nous allons la visualiser avec le code ci-dessous.

ggplot()+
  facet_grid(task_id ~ .)+
  geom_point(aes(
    classif.auc, learner_id),
    data=score_dt)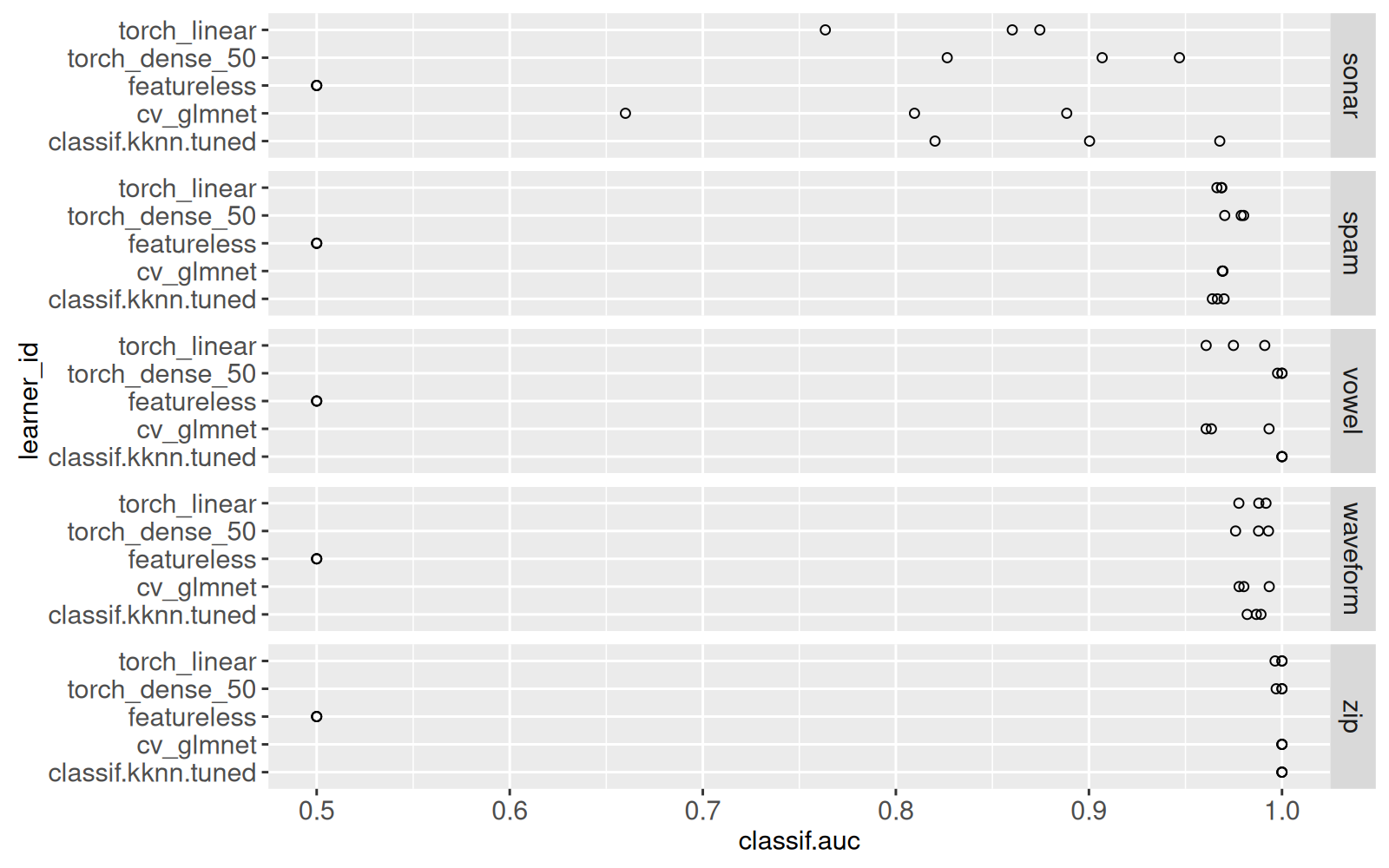

Le graphique ci-dessus affiche l’AUC sur l’ensemble test, pour chaque division de validation croisée, chaque jeu de données, et chaque algorithme d’apprentissage. Les résultats d’AUC suggèrent que zip est le plus facile d’apprendre, et sonar est le plus difficile d’apprendre, ce qui est consistant avec les taux d’erreur affichés dans le graphique précédent. Comme attendu, featureless (l’algorithme qui prédit toujours la classe majoritaire) a toujours AUC=0.5, ce qui correspond à une fonction de prédiction qui est constante. Le code ci-dessous retire les résultats de featureless, pour mettre en évidence les autres résultats.

ggplot()+
  facet_grid(task_id ~ .)+
  geom_point(aes(
    classif.auc, learner_id),
    data=score_dt[learner_id!="featureless"])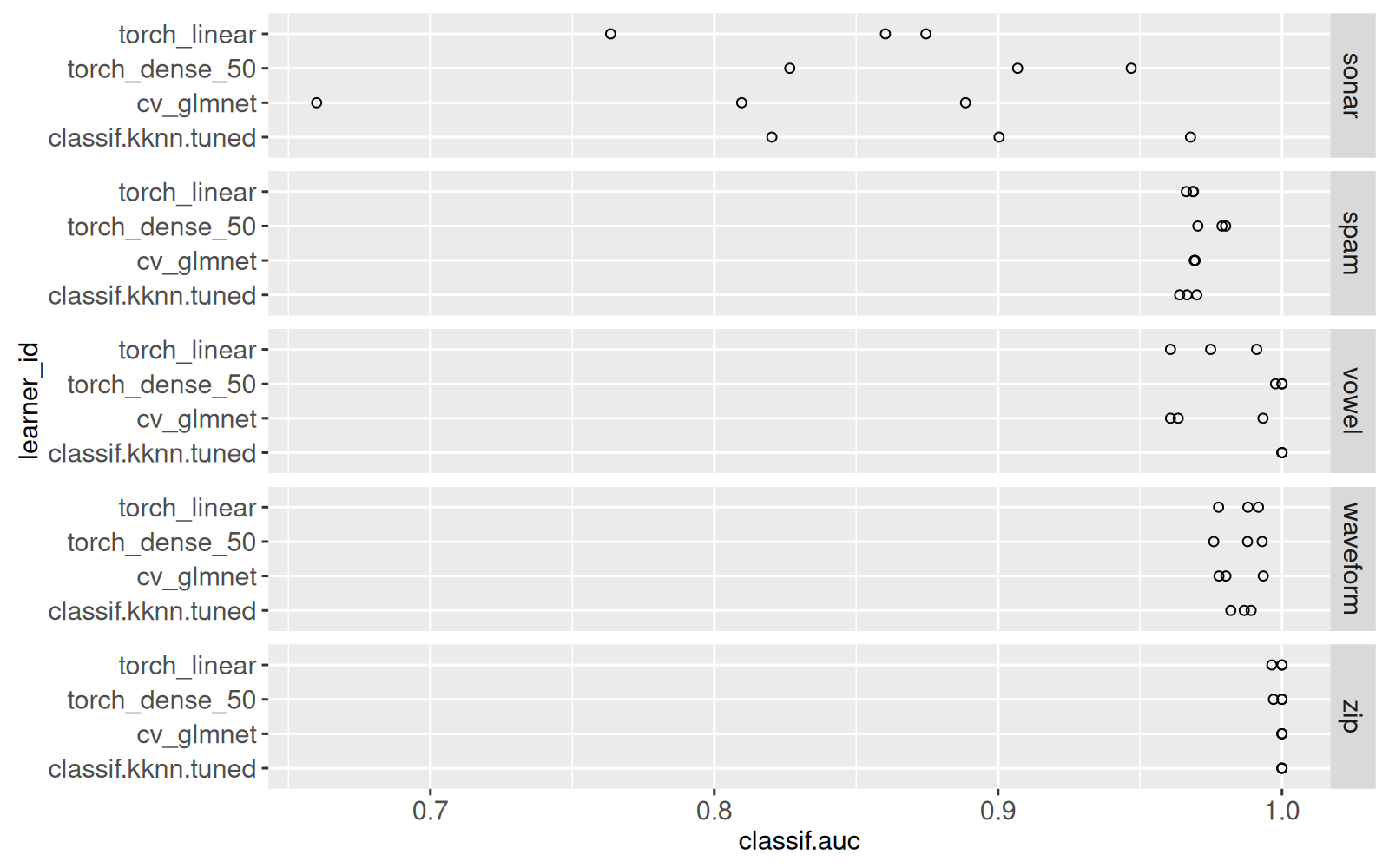

Nous ne voyons plus les résultats pour featureless dans le graphique ci-dessus. Le code ci-dessous produit le même graphique, avec quelques ajouts pour l’affichage interactif. Remarquons que la colonne task_it sera utile comme variable de sélection (pour à la fois task_id et iteration).

score_dt[, task_it := paste(task_id, iteration)]
(gg.auc <- ggplot()+
   theme_bw()+
   facet_grid(task_id ~ ., scales="free")+
   scale_x_continuous(
     "Test set Area Under the ROC Curve")+
   geom_point(aes(
     classif.auc*100, learner_id),
     clickSelects="task_it",
     size=5,
     fill="grey",
     color="black",
     color_off="grey",
     data=score_dt[learner_id!="featureless"]))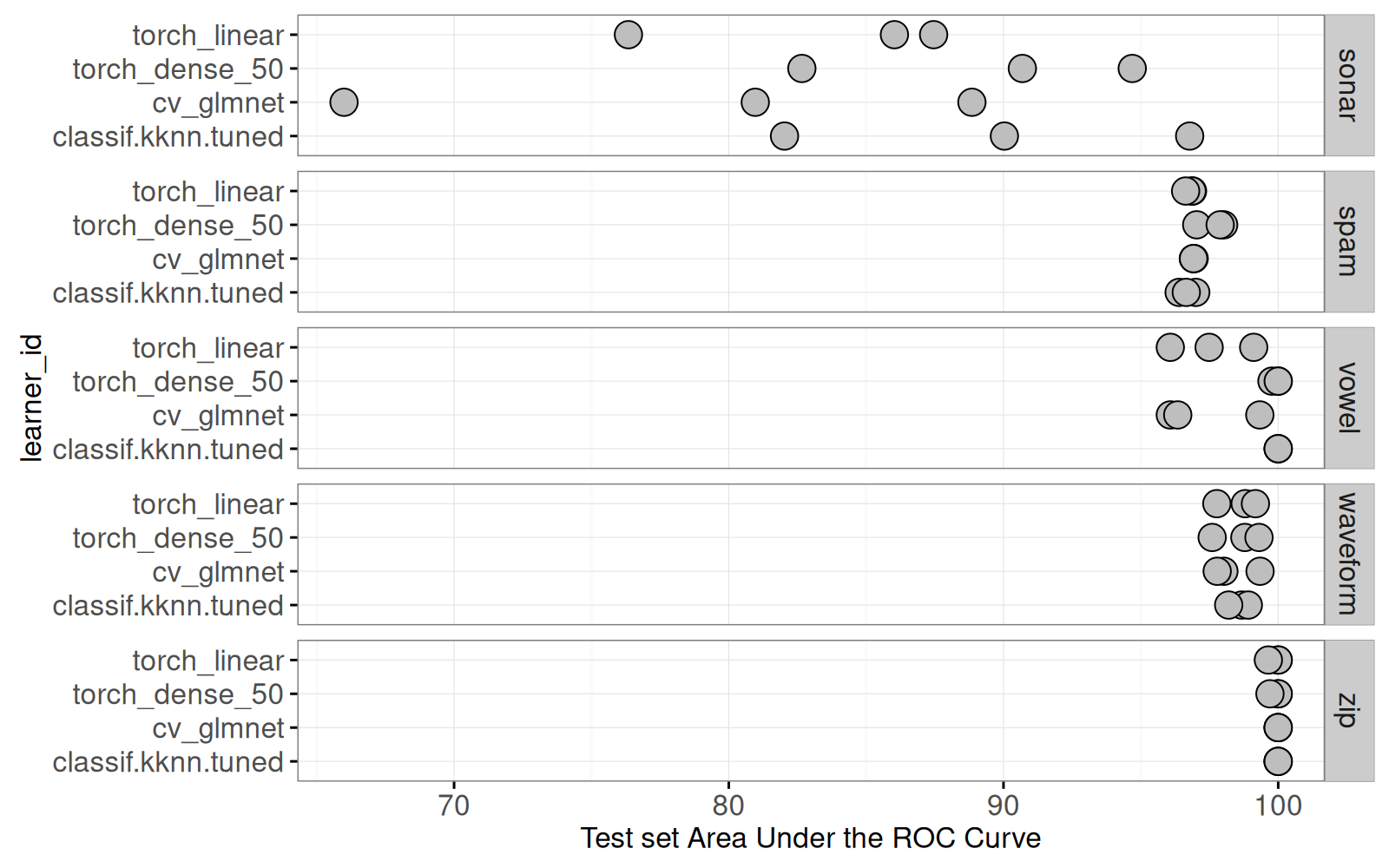

Nous calculons ensuite une courbe ROC pour chaque combinaison de task_id, learner_id et division de validation croisée (iteration). Remarquons que le vecteur d’étiquettes à prédire dans la classification binaire est un facteur à deux niveaux. Dans mlr3, le premier niveau est la classe positive, alors nous utilisons la première colonne de prob pour calculer la courbe ROC.

roc_dt <- score_dt[, {
  pred <- prediction_test[[1]]
  is.positive <- as.integer(pred$truth)==1
  label01 <- ifelse(is.positive, 1, 0)
  WeightedROC::WeightedROC(pred$prob[,1], label01)
}, by=.(task_id, learner_id, iteration, task_it)]
roc_dt[, .(task_it, learner_id, threshold, FPR, TPR)]

       task_it         learner_id   threshold       FPR       TPR
    1:  spam 1 classif.kknn.tuned 0.000000000 1.0000000 1.0000000
    2:  spam 1 classif.kknn.tuned 0.002703417 0.5190678 0.9949153
   ---                                                           
22470:   zip 3        featureless 0.503623188 1.0000000 1.0000000
22471:   zip 3        featureless         Inf 0.0000000 0.0000000

Le tableau ci-dessus représente les courbes ROC à utiliser pour évaluer les prédictions sur les ensembles test. Nous voyons que FPR=TPR=1 quand threshold=0, et que FPR=TPR=0 quand threshold=Inf. Le code ci-dessous affiche les courbes ROC dans différentes facettes.

gg.roc <- ggplot()+
  theme_bw()+
  geom_path(aes(
    FPR, TPR, group=learner_id, color=learner_id),
    data=roc_dt,
    showSelected="task_it")+
  scale_x_continuous(breaks=seq(0,1,by=0.5))+
  scale_y_continuous(breaks=seq(0,1,by=0.5))
gg.roc+facet_grid(iteration ~ task_id)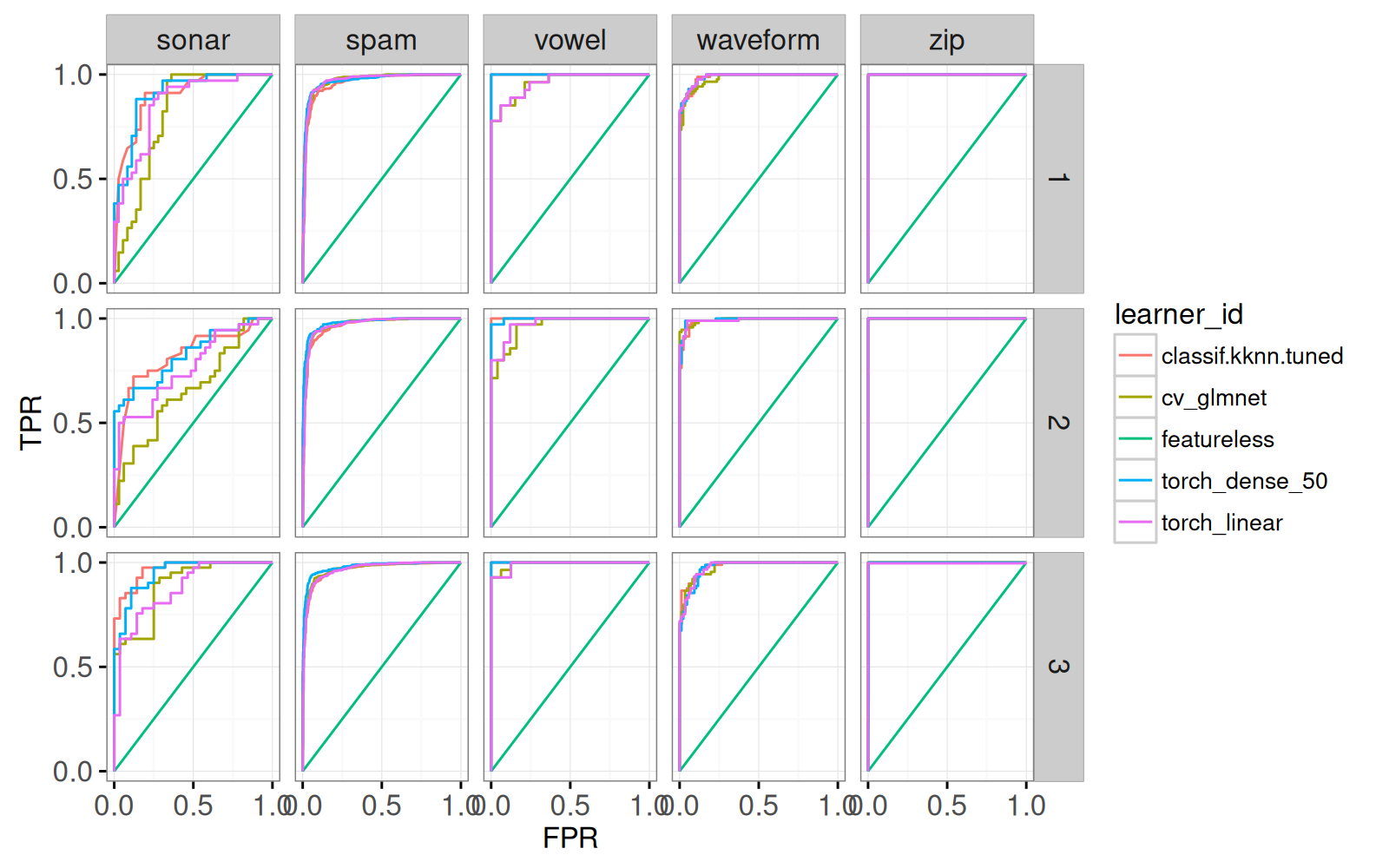

Nous voyons une facette pour chaque jeu de données et pour chaque division de validation croisée. Nous ajoutons maintenant un point pour montrer le seuil par défaut pour chaque algorithme.

gg.roc.point <- gg.roc+
  geom_point(aes(
    classif.fpr, classif.tpr, fill=learner_id,
    tooltip=sprintf(
      "%s default FPR=%.3f TPR=%.3f, errors=%.1f%%\n",
      learner_id, classif.fpr, classif.tpr, classif.ce*100)),
    data=score_dt,
    size=4,
    color="black",
    showSelected="task_it")
gg.roc.point+facet_grid(iteration ~ task_id)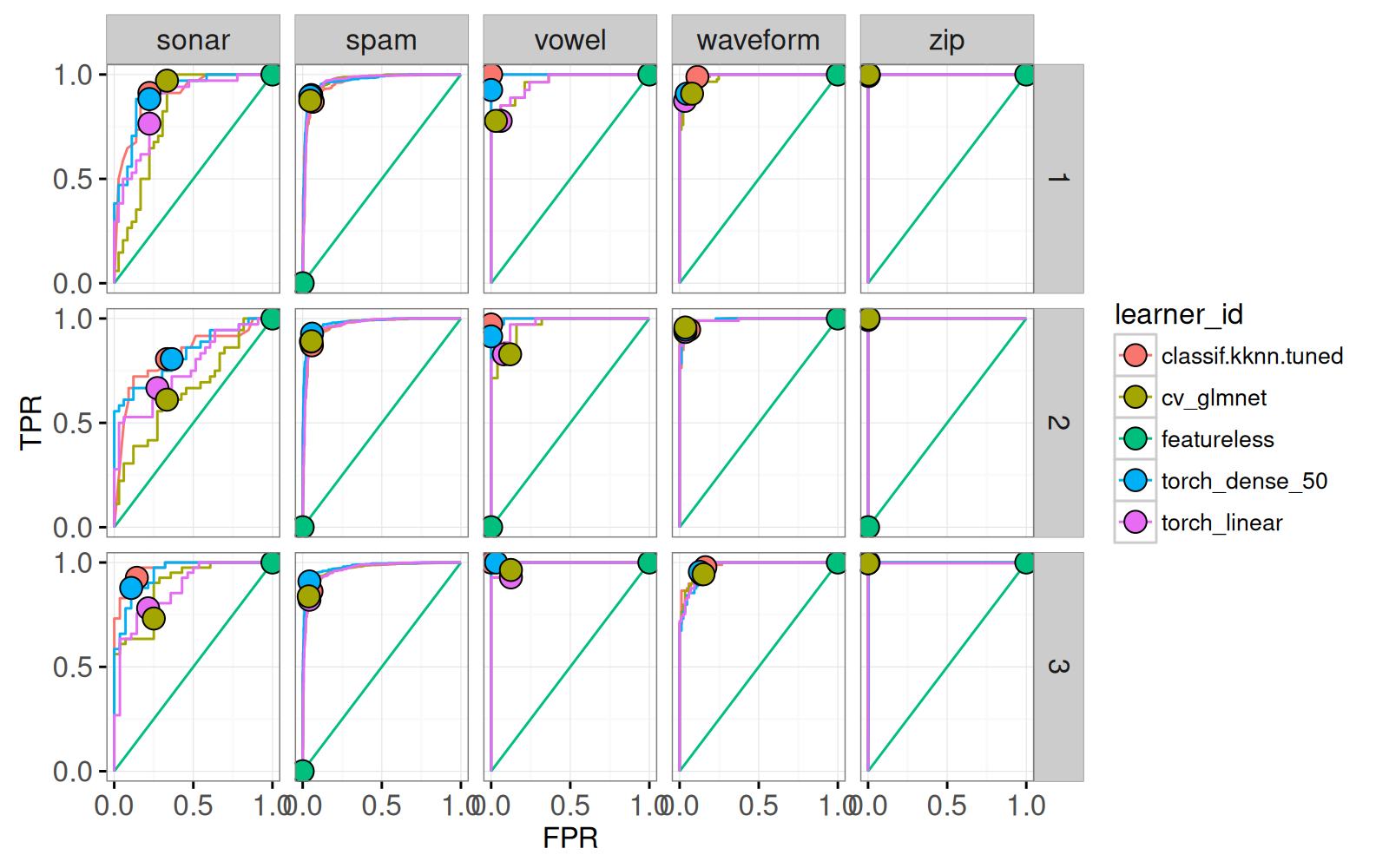

Ci-dessus nous voyons un point pour le seuil par défaut. Il est évident que les différents algorithmes ont différentes valeurs de FPR et TPR, par défaut. Nous ajoutons également du texte pour l’affichage de la sélection de données et de division de validation croisée.

score_dt[, lev_str := {
  pred <- prediction_test[[1]]
  paste(levels(pred$truth), collapse=" vs ")
}, by=task_id]
gg.roc.text <- gg.roc.point+
  geom_text(aes(
    0.5, 0,
    label=sprintf(
      "%s (%s) fold %d",
      task_id, lev_str, iteration)),
    data=score_dt[learner_id=="featureless"],
    showSelected="task_it")
gg.roc.text+facet_grid(iteration ~ task_id)

Le graphique affiche le texte sous chaque facette. Ensuite, nous calculons le rang de chaque algorithme dans chaque jeu de données et dans chaque division.

score_dt[
, auc.it.rank := rank(classif.auc)
, by=.(task_id, iteration, task_it)]

Les rangs calculés ci-dessus sont utilisés dans l’affichage qui suit. Nous créons une visualisation interactive à partir des graphiques de ROC et d’AUC.

animint(
  testAUC=gg.auc+
    ggtitle("Select data set and cross-validation split")+
    theme_animint(width=400, height=400),
  roc=gg.roc.text+
    ggtitle("ROC curves for selection")+
    theme_animint(width=400, height=400)+
    geom_label_aligned(aes(
      Inf, auc.it.rank*0.1, color=learner_id,
      label=sprintf("%s AUC=%.3f", learner_id, classif.auc)),
      data=score_dt,
      hjust=1,
      showSelected="task_it",
      alignment="vertical"))

Cliquer sur les points d’AUC de la visualisation, permet d’afficher les courbes ROC correspondantes en bas.

20.3.2 Interactivité des courbes ROC

Dans la section précédente, nous avons affiché un point sur chaque courbe ROC pour représenter le seuil par défaut. Ces points correspondent aux différents taux de faux positifs, pour les différents algorithmes d’apprentissage. Pour améliorer la justesse de la comparaison entre les algorithmes, nous affichons le meilleur taux de vrais positifs, pour un seuil de faux positifs donné (à définir dans la sélection interactive).

(best_TPR_dt <- roc_dt[, .(
  best_TPR=max(TPR)
), by=.(task_id,iteration,task_it,learner_id,FPR)])

       task_id iteration task_it         learner_id       FPR  best_TPR
    1:    spam         1  spam 1 classif.kknn.tuned 1.0000000 1.0000000
    2:    spam         1  spam 1 classif.kknn.tuned 0.5190678 0.9949153
   ---                                                                 
13134:     zip         3   zip 3        featureless 1.0000000 1.0000000
13135:     zip         3   zip 3        featureless 0.0000000 0.0000000

Le tableau ci-dessous contient le meilleur taux de vrais positifs (best_TPR), pour chaque seuil de faux positifs (FPR). Nous voulons afficher uniquement les seuils pour lesquels tous les algorithmes sont présents, nous comptons donc les algorithmes pour chaque seuil.

best_TPR_algos <- best_TPR_dt[, .(
  algos = .N
), by=.(task_id,iteration,task_it,FPR)]
table(best_TPR_algos$algos)

   1    2    3    4    5 
  47  262 2498 1230   30 

Remarquons que dans le tableau ci-dessus

• il y a 30 seuils extrêmes pour lesquels les 5 algorithmes sont présents (y compris featureless),
• il y a plusieurs seuils avec 3 algorithmes ou moins et nous ne voulons pas les afficher. Nous voulons conserver uniquement les seuils associés à au moins 4 algorithmes; le code ci-dessous nous le permet. De plus, pour faciliter la sélection interactive, nous limitons le nombre de seuils à 40, répartis de manière quasi uniforme parmi les valeurs possibles pour le taux de faux positifs.

(min.algos <- length(learner.list)-1)

[1] 2

max.FPR.values <- 40
(FPR_vlines <- best_TPR_algos[algos >= min.algos][
, keep := c(TRUE, diff(ceiling(FPR*max.FPR.values))!=0)
, by=.(task_id,iteration,task_it)][keep==TRUE])

     task_id iteration task_it        FPR algos keep
  1:    spam         1  spam 1 1.00000000     5 TRUE
  2:    spam         1  spam 1 0.51906780     4 TRUE
 ---                                                
648:     zip         3   zip 3 0.04761905     3 TRUE
649:     zip         3   zip 3 0.02197802     3 TRUE

Le tableau ci-dessus contient les seuils sélectionnables avec l’interactivité. Dans le code ci-dessous, nous représentons chaque seuil par une ligne verticale.

gg.roc.fpr <- gg.roc.text+
  geom_vline(aes(
    xintercept=FPR),
    alpha=0.7,
    size=5,
    data=FPR_vlines,
    showSelected="task_it",
    clickSelects="FPR")
gg.roc.fpr+facet_grid(iteration ~ task_id)

Le graphique ci-dessus affiche une ligne verticale pour chaque seuil, si bien qu’il apparaît entièrement noir. Nous créons ensuite un nouveau graphique pour afficher les meilleurs taux de vrais positifs, pour le seuil sélectionné.

best_TPR_show <- best_TPR_dt[
  FPR_vlines, on=.(task_id,iteration,task_it,FPR)]
(gg.tpr <- ggplot()+
   theme_bw()+
   theme(legend.position="none")+
   geom_point(aes(
     best_TPR, learner_id, color=learner_id),
     data=best_TPR_show,
     size=5,
     showSelected=c("task_it","FPR"))+
   geom_text(aes(
     best_TPR, learner_id, label=sprintf("%.4f", best_TPR)),
     data=best_TPR_show,
     showSelected=c("task_it","FPR")))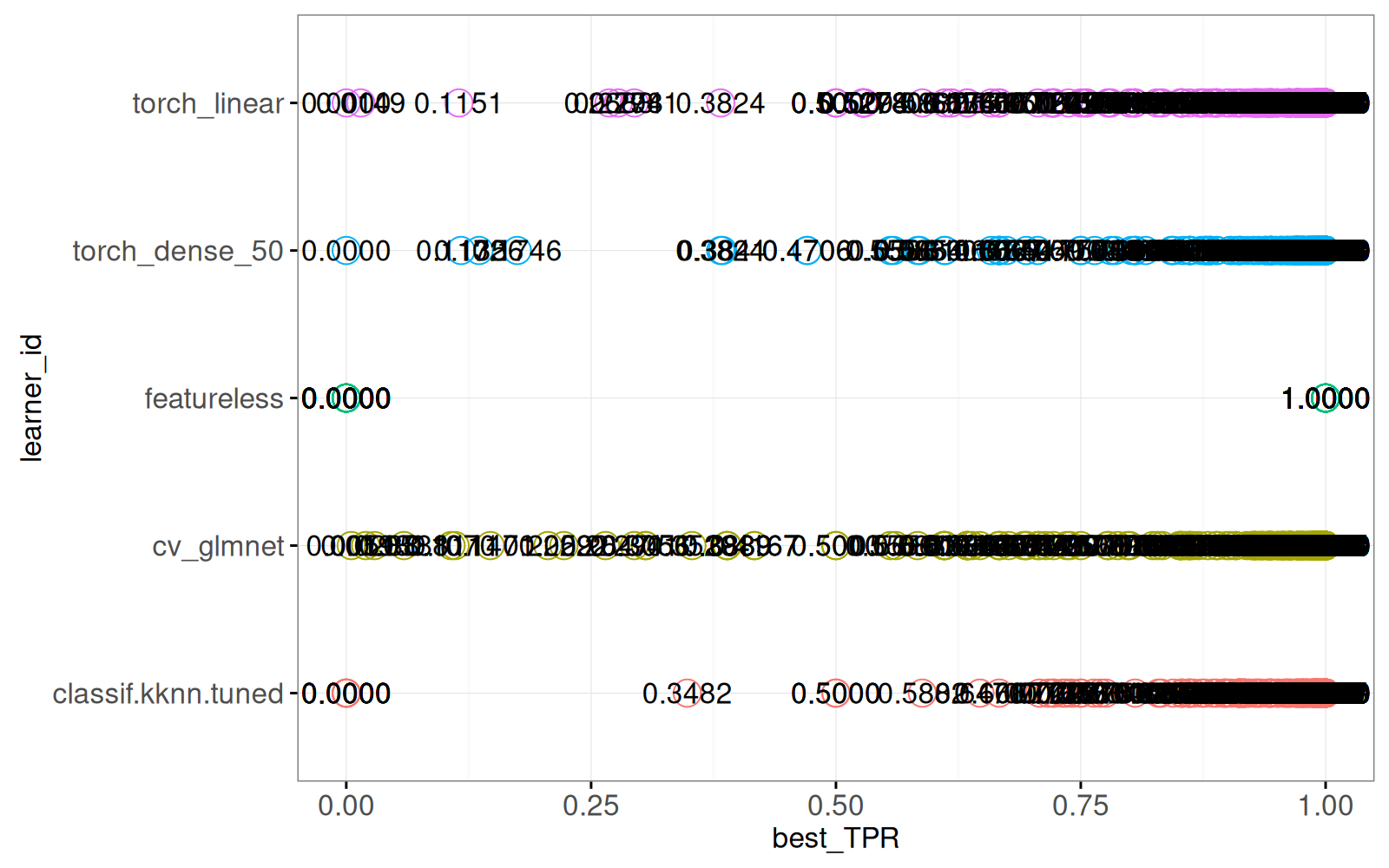

Le graphique ci-dessus affiche un point et du texte pour les meilleurs taux de vrais positifs. Puis nous combinons tous les graphiques précédents dans une visualisation interactive.

(viz.select.fpr <- animint(
  testAUC=gg.auc+
    ggtitle("Select data set and cross-validation split"),
  roc=gg.roc.fpr+
    ggtitle("ROC curves for selection")+
    theme_animint(last_in_row=TRUE),
  TPR=gg.tpr+
    ggtitle("Best TPR for selected FPR")+
    theme_animint(colspan=2, width=800, height=200)))

La visualisation ci-dessus permet de

• cliquer sur le graphique en haut à gauche pour choisir un jeu de données et une division de validation croisée (task_it);
• cliquer sur le graphique en haut à droite pour choisir un seuil de taux de faux positifs (FPR);
• visualiser les meilleurs taux de vrais positifs, dans le graphique du bas.

En cliquant sur les seuils de FRP dans les données sonar, vous verrez que le meilleur algorithme dépend du seuil choisi. Par exemple, cv_glmnet est le moins bon pour un FPR faible, mais il est le meilleur pour un FPR plus élevé.

20.3.3 Ajout d’un niveau de zoom

Les visualisations précédentes recouraient à des facettes pour afficher l’AUC des différents jeux de données. Dans cette section, nous proposons d’afficher l’AUC pour un seul jeu de données à la fois. Nous créerons un graphique permettant de sélectionner un jeu de données en fonction du nombre d’observations, et de l’AUC maximale, valeurs que nous calculons avec le code ci-dessous.

(summary_dt <- score_dt[, .(
  max_auc=max(classif.auc),
  nrow=task[[1]]$nrow
), by=task_id])

    task_id   max_auc nrow
1:     spam 0.9801429 4601
2:    sonar 0.9677700  208
3:    vowel 1.0000000  180
4: waveform 0.9933929  527
5:      zip 1.0000000 1655

Le tableau ci-dessus contient une ligne pour chaque jeu de données. Nous utilisons ce tableau pour dessiner le nuage de points ci-dessous.

point_size <- 5
point_fill <- "grey"
point_color <- "black"
point_color_off <- "grey"
(gg.summary <- ggplot()+
  theme_bw()+
  geom_point(aes(
    nrow, max_auc),
    size=point_size,
    fill=point_fill,
    color=point_color,
    color_off=point_color_off,
    clickSelects="task_id",
    data=summary_dt))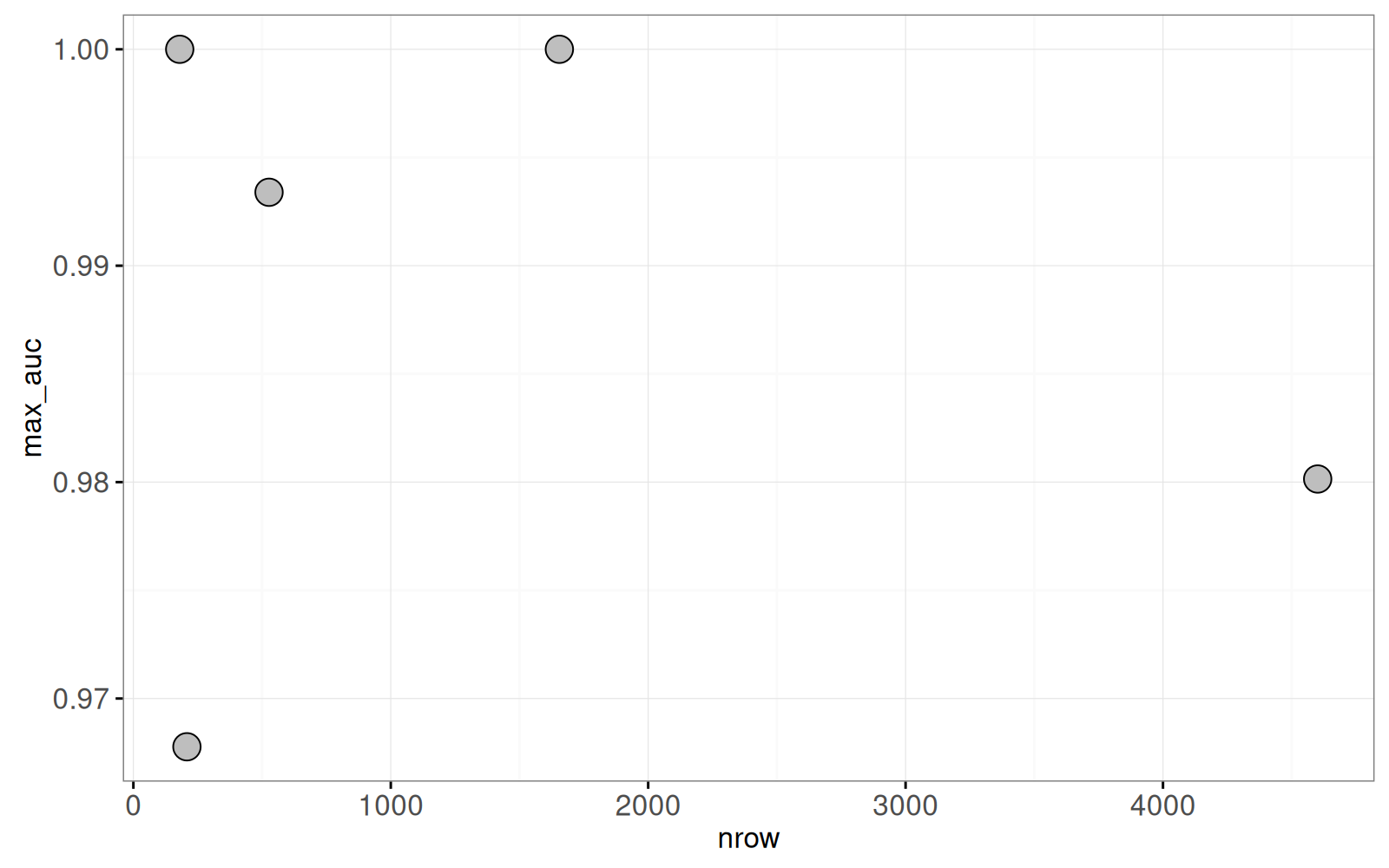

Le graphique contient un point pour chaque jeu de données. Remarquons que, dans le code ci-dessus, le paramètre clickSelects="task_id", permet uniquement la sélection d’un jeu de données (et non de la division de validation croisée). Nous créons ensuite un graphique avec showSelected="task_id" et clickSelects="iteration".

gg.auc.show.task <- ggplot()+
  theme_bw()+
  geom_point(aes(
    classif.auc, learner_id),
    clickSelects="iteration",
    showSelected="task_id",
    size=point_size,
    fill=point_fill,
    color=point_color,
    color_off=point_color_off,
    data=score_dt)
gg.auc.show.task+facet_grid(task_id ~ .)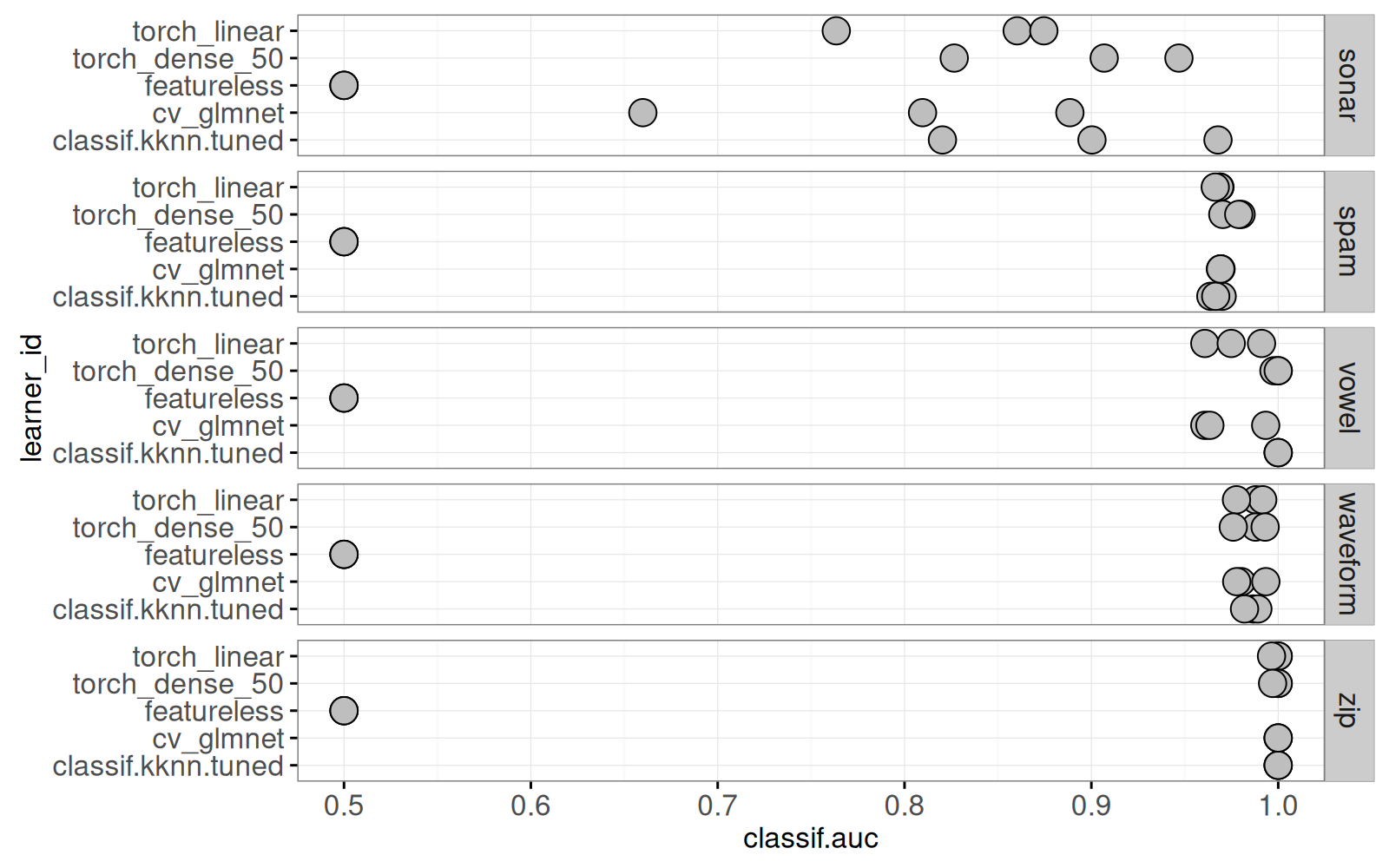

Le graphique contient un panneau pour chaque jeu de données. Nous constatons que les valeurs d’AUC varient énormément d’un jeu de données à l’autre, et que featureless a toujours une AUC de 0.5, comme prévu. Nous supprimons featureless dans le graphique ci-dessous.

gg.auc.show.task.zoom <- ggplot()+
  theme_bw()+
  geom_point(aes(
    classif.auc, learner_id),
    clickSelects="iteration",
    showSelected="task_id",
    size=point_size,
    fill=point_fill,
    color=point_color,
    color_off=point_color_off,
    data=score_dt[learner_id != "featureless"])
gg.auc.show.task.zoom+facet_grid(task_id ~ .)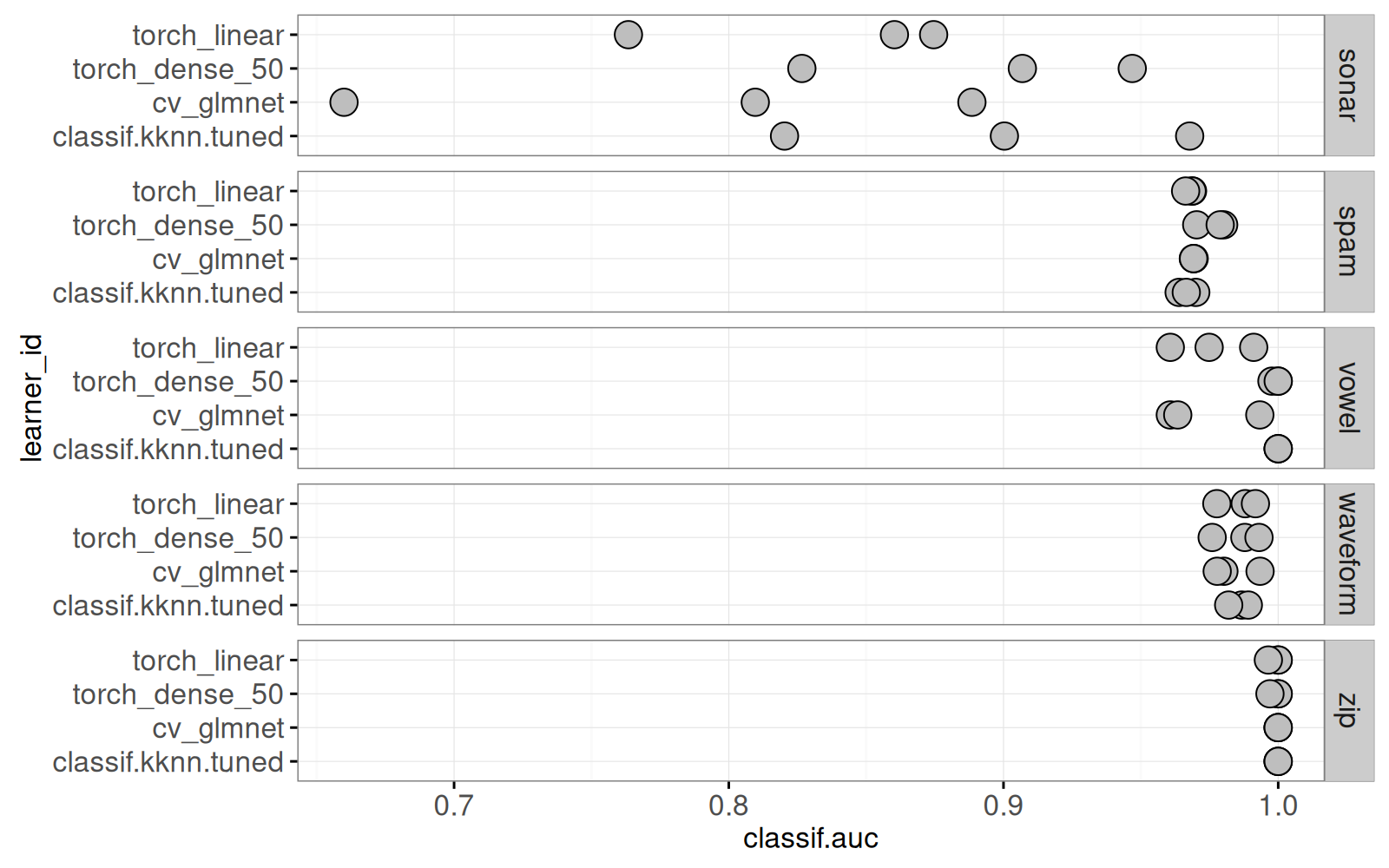

Le graphique ci-dessus ne contient plus featureless. Nous créons maintenant un graphique des courbes ROC pour la sélection de task_id et iteration.

gg.roc.show.task.it <- ggplot()+
  theme_bw()+
  geom_path(aes(
    FPR, TPR, group=learner_id, color=learner_id),
    data=roc_dt,
    showSelected=c("task_id","iteration"))+
  scale_x_continuous(breaks=seq(0,1,by=0.5))+
  scale_y_continuous(breaks=seq(0,1,by=0.5))
gg.roc.show.task.it+facet_grid(iteration ~ task_id)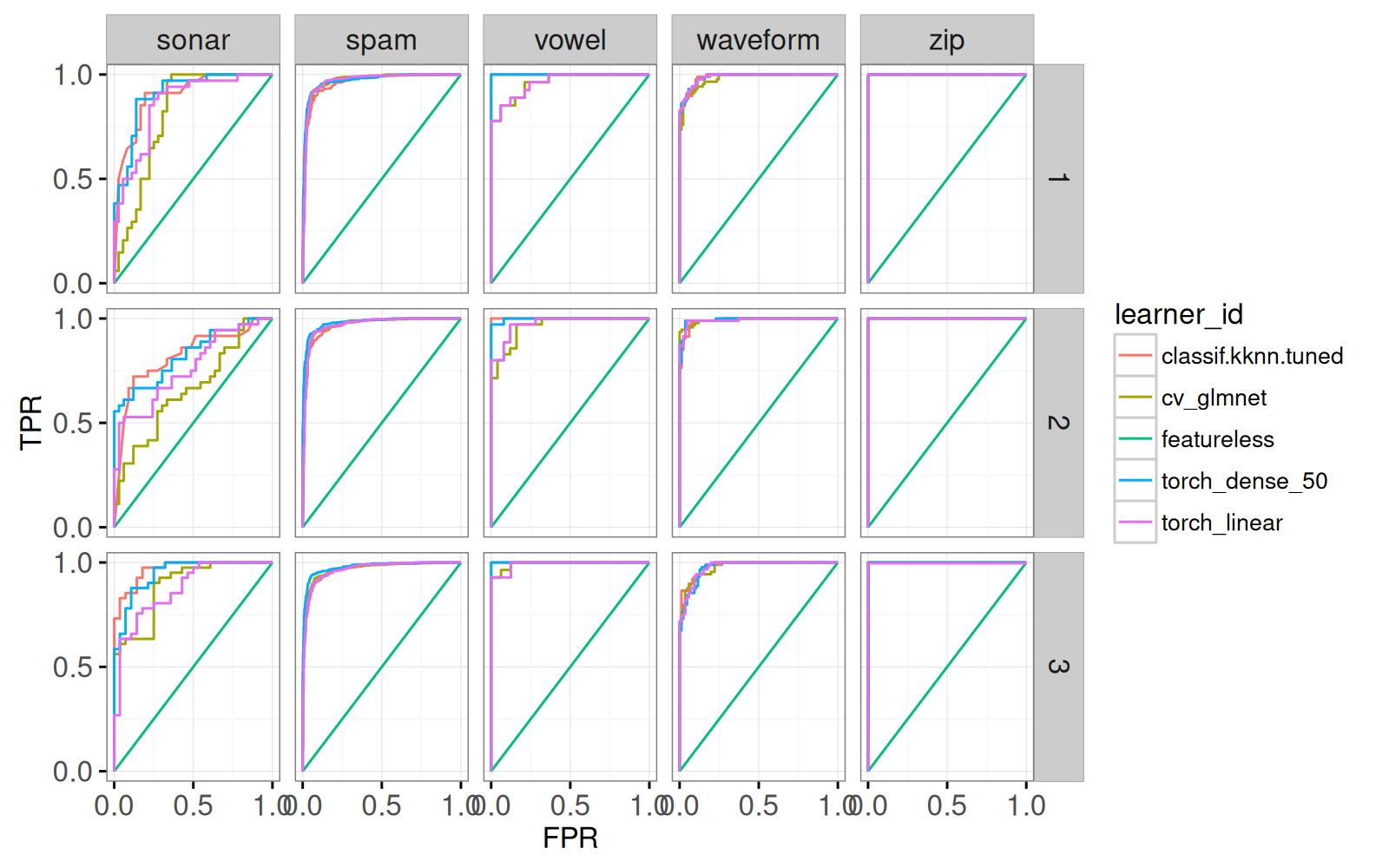

Le graphique affiche un panneau pour chaque jeu de données, et pour chaque division de validation croisée. Le code ci-dessous combine ces graphiques dans une visualisation interactive.

animint(
  summary=gg.summary+
    ggtitle("1. Select task"),
  roc=gg.roc.show.task.it+
    ggtitle("ROC curves for selected task and iteration")+
    theme_animint(last_in_row=TRUE),
  testAUC=gg.auc.show.task+
    ggtitle("2. Select iteration, all learners")+
    theme_animint(
      width=800, height=200, last_in_row=TRUE, colspan=2),
  testAUCzoom=gg.auc.show.task.zoom+
    ggtitle("2. Select iteration, zoom to non-trivial")+
    theme_animint(
      update_axes="x",
      width=800, height=200, last_in_row=TRUE, colspan=2))

Le graphique affiche

• en haut à gauche, un résumé de tous les jeux de données (cliquez sur un point pour sélectionner un jeu de données).
• en bas, deux graphiques de l’AUC pour les ensembles test, pour le jeu de données sélectionné (cliquez sur un point pour sélectionner une division de validation croisée).
• en haut à droite, les courbes ROC pour la sélection de task_id et iteration.

20.3.4 Tests statistiques pour différences entre algorithmes

Il est souvent utile de déterminer s’il existe des différences significatives entre l’AUC de deux algorithmes (les deux ayant l’AUC la plus grande). Dans cette section, nous calculons des valeurs p pour déterminer si les différences sont significatives. Nous calculons d’abord la moyenne et l’écart type, des divisions de validation croisée.

(score_stats <- dcast(
  score_dt[learner_id!="featureless"],
  task_id + learner_id ~ .,
  list(mean, sd),
  value.var="classif.auc"))

    task_id         learner_id classif.auc_mean classif.auc_sd
 1:   sonar classif.kknn.tuned        0.8961277    0.073831533
 2:   sonar          cv_glmnet        0.7860250    0.116100073
---                                                           
19:     zip     torch_dense_50        0.9989899    0.001726940
20:     zip       torch_linear        0.9987966    0.002061654

Nous visualisons ces statistiques grâce au code ci-dessous.

score_stats[, let(
  lo=classif.auc_mean-classif.auc_sd,
  hi=classif.auc_mean+classif.auc_sd)]
ggplot()+
  facet_grid(task_id ~ .)+
  geom_point(aes(
    classif.auc_mean, learner_id),
    data=score_stats)+
  geom_segment(aes(
    hi, learner_id,
    xend=lo, yend=learner_id),
    data=score_stats)+
  scale_x_continuous(
    "Test AUC (mean ± SD over 3 folds in CV)",
    breaks=seq(0,1,by=0.1))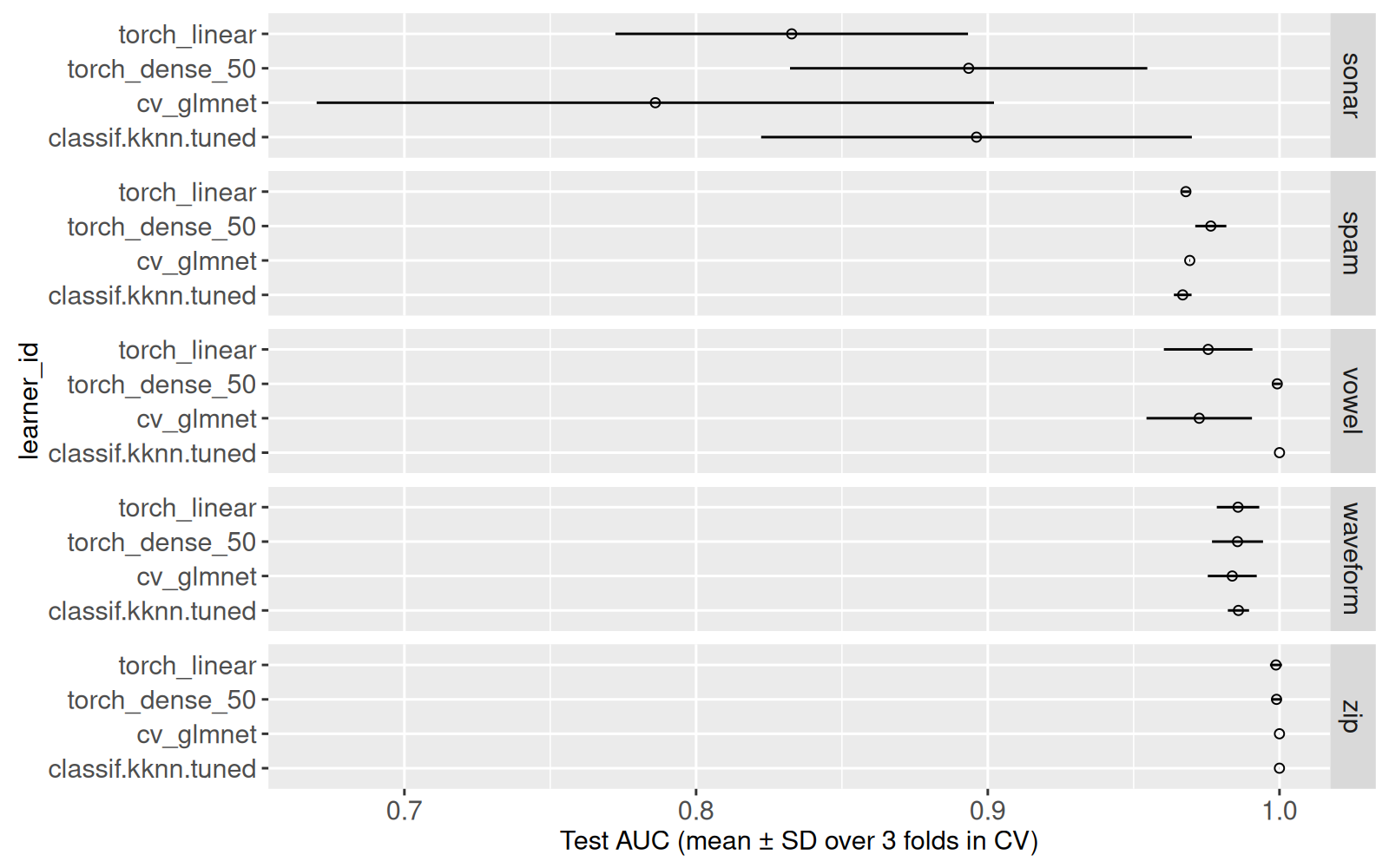

Ci-dessus nous voyons un point pour chaque moyenne, et un segment pour l’écart type. Ensuite nous calculons le rang de chaque algorithme, pour chaque jeu de données.

score_stats[, auc.task.rank := rank(-classif.auc_mean), by=task_id][]

    task_id         learner_id classif.auc_mean classif.auc_sd        lo
 1:   sonar classif.kknn.tuned        0.8961277    0.073831533 0.8222961
 2:   sonar          cv_glmnet        0.7860250    0.116100073 0.6699249
---                                                                     
19:     zip     torch_dense_50        0.9989899    0.001726940 0.9972629
20:     zip       torch_linear        0.9987966    0.002061654 0.9967349
           hi auc.task.rank
 1: 0.9699592             1
 2: 0.9021250             4
---                        
19: 1.0007168             3
20: 1.0008583             4

Ci-dessus nous voyons une nouvelle colonne auc.task.rank qui présente des valeurs entre 1 et 4. Nous utilisons ces valeurs sur l’axe Y dans le graphique ci-dessous.

gg.rank <- ggplot()+
  geom_point(aes(
    classif.auc_mean, auc.task.rank),
    data=score_stats)+
  geom_segment(aes(
    classif.auc_mean+classif.auc_sd, auc.task.rank,
    xend=classif.auc_mean-classif.auc_sd, yend=auc.task.rank),
    data=score_stats)+
  scale_y_continuous(
    "Algorithm rank using test AUC",
    breaks=1:4,
    limits=c(1,5))+
  scale_x_continuous(
    "Test AUC (mean ± SD over 3 folds in CV)")
gg.rank+facet_wrap("task_id", scales="free")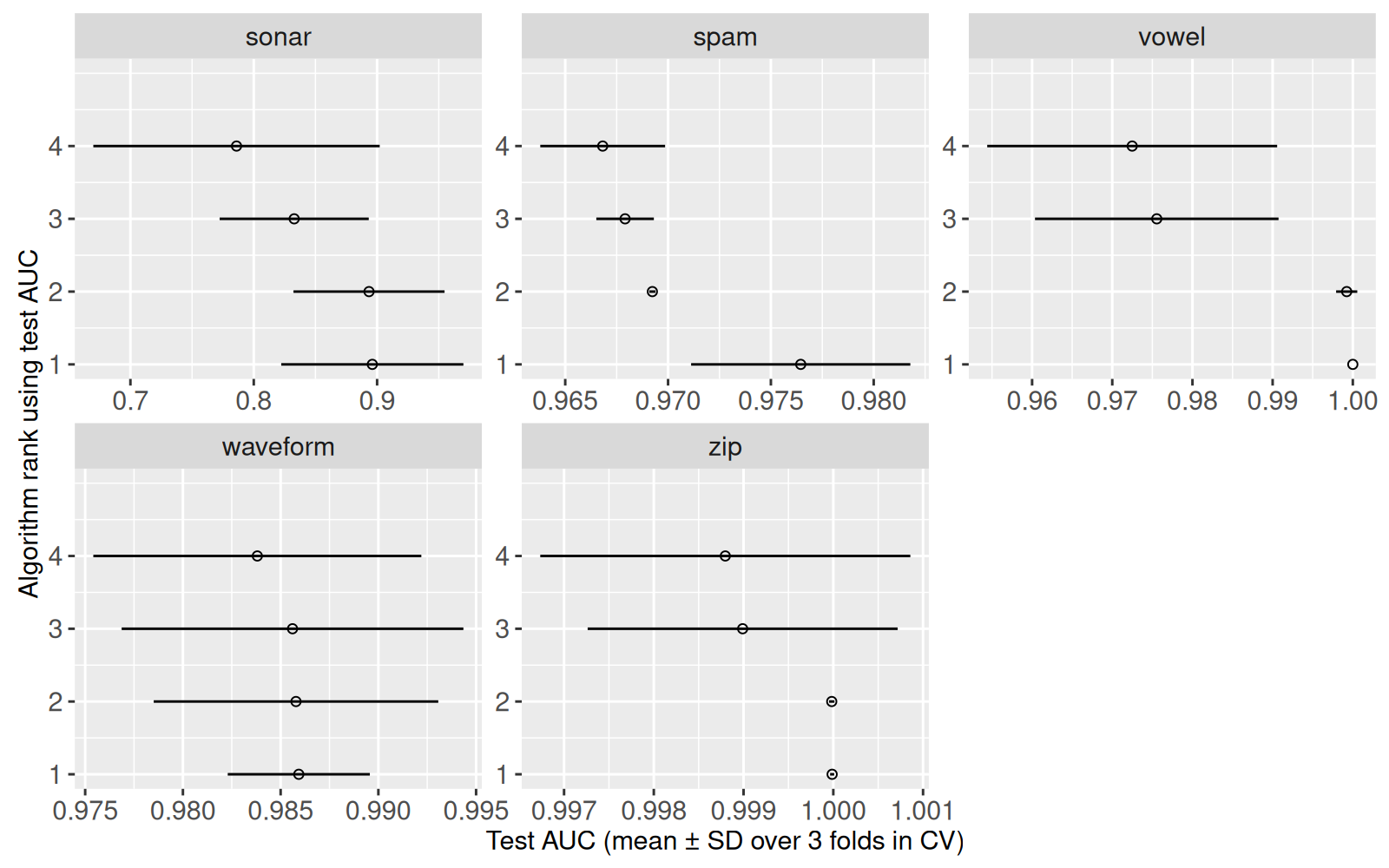

Ci-dessus nous voyons les rangs, mais pas les noms. Nous ajoutons les noms ci-dessous.

gg.rank.text <- gg.rank+
  geom_text(aes(
    -Inf, auc.task.rank,
    label=sprintf(
      "%s %.4f±%.4f",
      learner_id,
      classif.auc_mean, classif.auc_sd)),
    hjust=0, vjust=-0.5, size=10,
    data=score_stats)
gg.rank.text+facet_wrap("task_id", scales="free")

Pour tester les différences entre les rangs adjacents, nous faisons une jointure entre chaque rang (auc.task.rank) et le rang suivant (next.rank).

score_dt_rank <- score_stats[, .(auc.task.rank, learner_id, task_id)][
  score_dt, on=.(learner_id, task_id), nomatch=0L
][order(task_id, auc.task.rank)]
(join_dt <- score_dt_rank[, next.rank := auc.task.rank+1][
  score_dt_rank, .(
    task_id, iteration,
    good.rank=i.auc.task.rank, bad.rank=x.auc.task.rank,
    good.auc =i.classif.auc,   bad.auc =x.classif.auc),
  on=.(task_id, iteration, auc.task.rank=next.rank),
  nomatch=0L])

    task_id iteration good.rank bad.rank  good.auc   bad.auc
 1:   sonar         1         1        2 0.9003268 0.9068627
 2:   sonar         2         1        2 0.8202862 0.8265993
---                                                         
44:     zip         2         3        4 1.0000000 1.0000000
45:     zip         3         3        4 0.9969958 0.9964161

Ensuite nous effectuons des tests de Student.

(pval_dt <- join_dt[, .SDcols=c("good.auc","bad.auc"), {
  mean_dt <- lapply(.SD, mean)
  paired <- t.test(
    bad.auc, good.auc, alternative = "l", paired=TRUE)
  c(mean_dt, p.paired=paired$p.value)
}, keyby=.(task_id, good.rank, bad.rank)])

    task_id good.rank bad.rank  good.auc   bad.auc    p.paired
 1:   sonar         1        2 0.8961277 0.8934421 0.397970335
 2:   sonar         2        3 0.8934421 0.8327755 0.007528393
---                                                           
14:     zip         2        3 0.9999825 0.9989899 0.213858957
15:     zip         3        4 0.9989899 0.9987966 0.211324865

Le tableau ci-dessus contient une ligne pour chaque test statistique. Ci-dessous, nous rajoutons des segments rouges pour souligner les différences entre les moyennes.

gg.rank.seg <- gg.rank+
  geom_segment(aes(
    bad.auc, good.rank+0.5,
    xend=good.auc, yend=good.rank+0.5),
    color="red",
    data=pval_dt)
gg.rank.seg+facet_wrap("task_id", scales="free")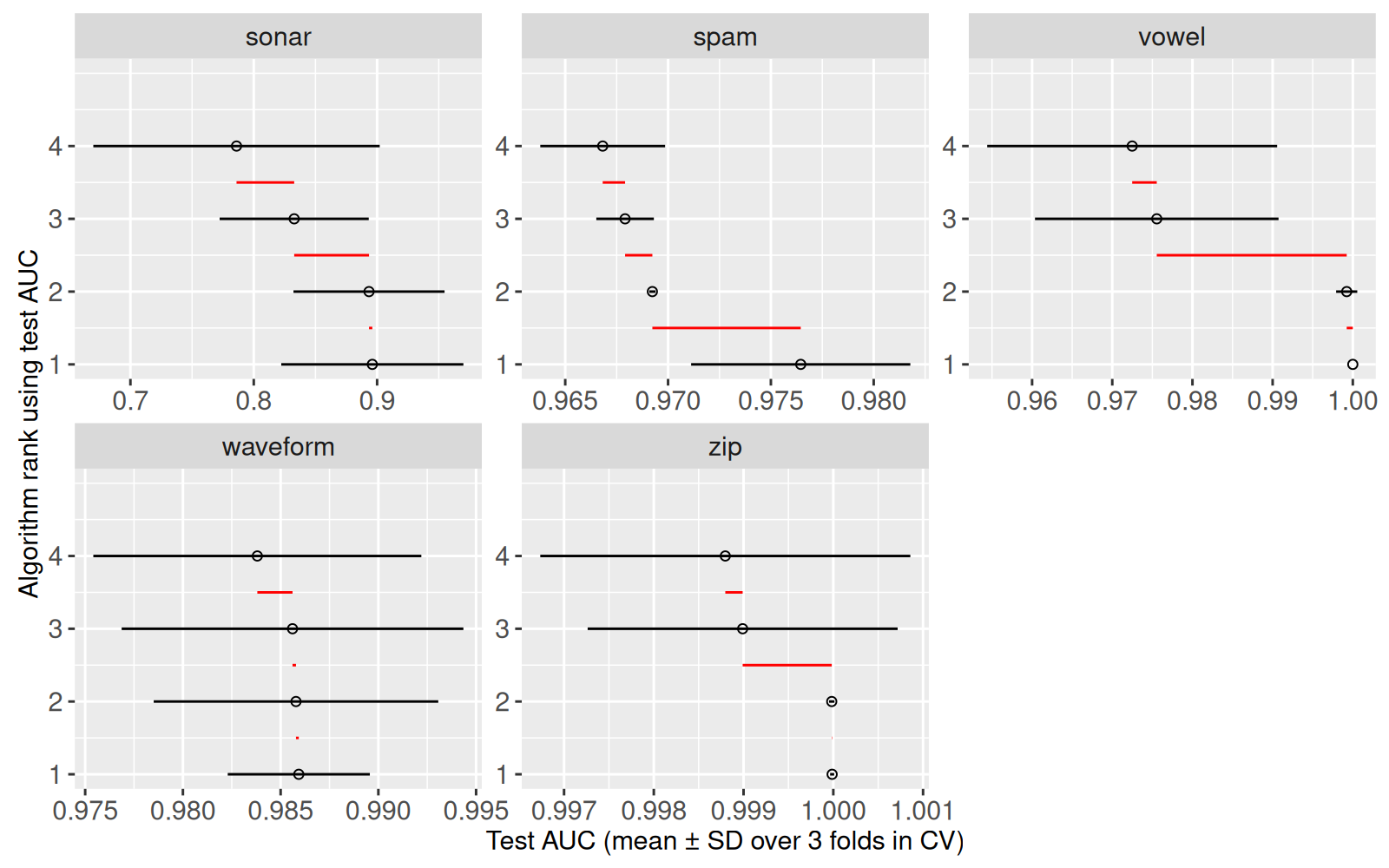

Ci-dessus nous voyons un segment pour chaque test statistique. Nous rajoutons ensuite des éléments de texte pour afficher les valeurs p.

gg.rank.p <- gg.rank.seg+
  geom_text(aes(
    bad.auc, good.rank+0.5, label=ifelse(
      p.paired<0.01, "P<0.01",
      sprintf("P=%.2f", p.paired))),
    color="red", hjust=1, size=10,
    data=pval_dt)
gg.rank.p+facet_wrap("task_id", scales="free")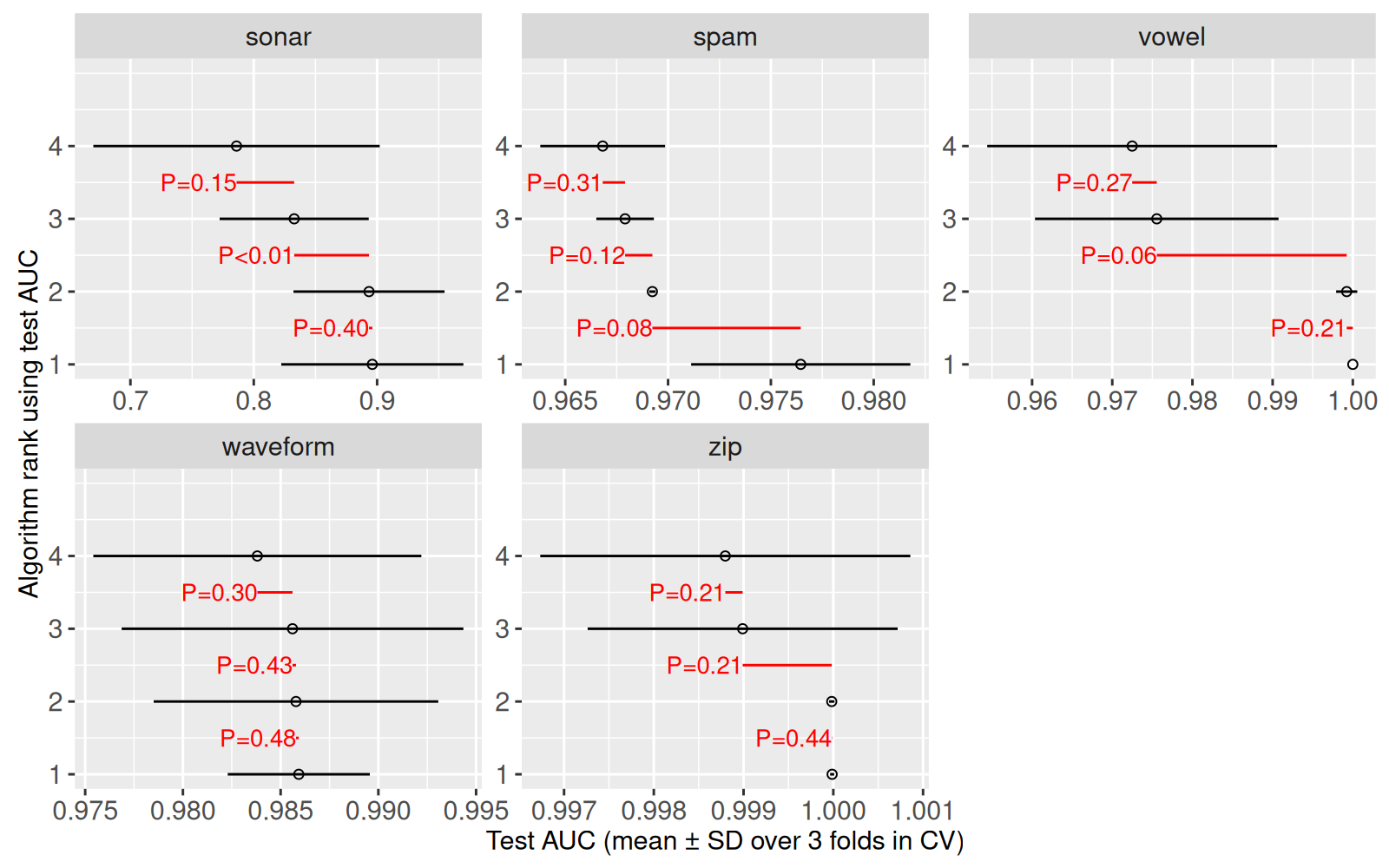

Le graphique affiche les valeurs p.

• Une des valeur p est inférieure à 1% (P<0.01), ce qui indique une différence significative, entre les rangs 2 et 3 dans les données sonar.
• Les autres valeurs p sont supérieures à 5% (P>0.05), ce qui indique des différences non-significatives.
• L’absence de différences significatives est partiellement due à la taille réduite de l’échantillon utilisé pour le test de Student (seulement 3 divisions de validation croisée). Vous pourriez éventuellement obtenir des valeurs p plus petites en augmentant le nombre de divisions de validation croisée (voir exercice).
• Exercice : afficher les valeurs p avec le nom des algorithmes et les statistiques (moyenne et écart type) sur le même graphique. Utilisez ce graphique au lieu de testAUCzoom dans la visualisation précédente.

20.4 Vérification de la régularisation

Dans cette section, nous voulons créer des graphiques pour vérifier que les algorithmes sont régularisés correctement. Chaque algorithme d’apprentissage utilise une méthode différente de régularisation, et différents hyperparamètres pour éviter à la fois le surapprentissage et le sous-apprentissage.

• Pour les plus proches voisins, il faut augmenter le nombre de voisins pour régulariser. Un petit nombre de voisins peut donner un surapprentissage, et un grand nombre de voisins peut donner un sous-apprentissage.
• Pour les algorithmes de torch, il faut réduire le nombre d’époques de descente de gradient pour régulariser. Un petit nombre d’époques peut donner un sous-apprentissage, et un grand nombre d’époques peut donner un surapprentissage.
• Pour le modèle lineaire avec régularisation L1 (glmnet), il faut augmenter la pénalité pour régulariser. Une petite pénalité peut donner un surapprentissage, et une grande penalité peut donner un sous-apprentissage.

20.4.1 Plus proches voisins

Dans cette section, nous vérifions le choix de nombre de voisins. Normalement, pour chaque division des données en test et entraînement, nous faisons ensuite une division d’entraînement en sous-entraînement et validation. Nous voulons choisir le nombre de voisins qui maximise l’AUC sur l’ensemble de validation, et ensuite utiliser ce nombre de voisins pour calculer les prédictions sur l’ensemble test. Pour chaque ensemble test, il y pourrait avoir un différent nombre de voisins. Nous commençons par calculer un tableau avec une ligne par division de validation croisée, et une colonne avec le nombre de voisins.

(best_dt <- score_dt[grep("knn", learner_id), {
  arch <- learner[[1]]$archive
  adata <- arch$data[, status := ifelse(
    classif.auc==max(classif.auc), "max", "other")]
  arch$best()[, .(k, details=list(adata))]
}, by=.(task_id, iteration, task_it)])

    task_id iteration task_it  k             details
 1:    spam         1  spam 1 14 <data.table[10x10]>
 2:    spam         2  spam 2 27 <data.table[10x10]>
---                                                 
14:     zip         2   zip 2 23 <data.table[10x10]>
15:     zip         3   zip 3 18 <data.table[10x10]>

Le tableau contient les colonnes

• k, le nombre de voisins choisi pour maximiser l’AUC sur l’ensemble de validation.
• details, un tableau d’informations sur le choix du nombre de voisins.

Ensuite, nous faisons un tableau qui combine les détails pour chaque division.

details_dt <- best_dt[
, details[[1]][order(k)]
, by=.(task_id, iteration, task_it)]
details_dt[, .(task_id, iteration, k, classif.auc, status)]

     task_id iteration  k classif.auc status
  1:    spam         1  1   0.8952152  other
  2:    spam         1  5   0.9536615  other
 ---                                        
149:     zip         3 36   0.9999803    max
150:     zip         3 40   0.9999803    max

Le tableau ci-dessus contient une ligne pour chaque nombre de voisins testé sur les ensembles de validation. Ensuite nous visualisons l’AUC sur l’ensemble de validation, en fonction du nombre de voisins.

gg.neighbors <- ggplot()+
  geom_vline(aes(
    xintercept=k),
    showSelected="task_it",
    data=best_dt)+
  geom_point(aes(
    k, classif.auc, color=status),
    showSelected="task_it",
    data=details_dt)+
  scale_y_continuous("Validation set AUC")
gg.neighbors+facet_grid(task_id ~ iteration)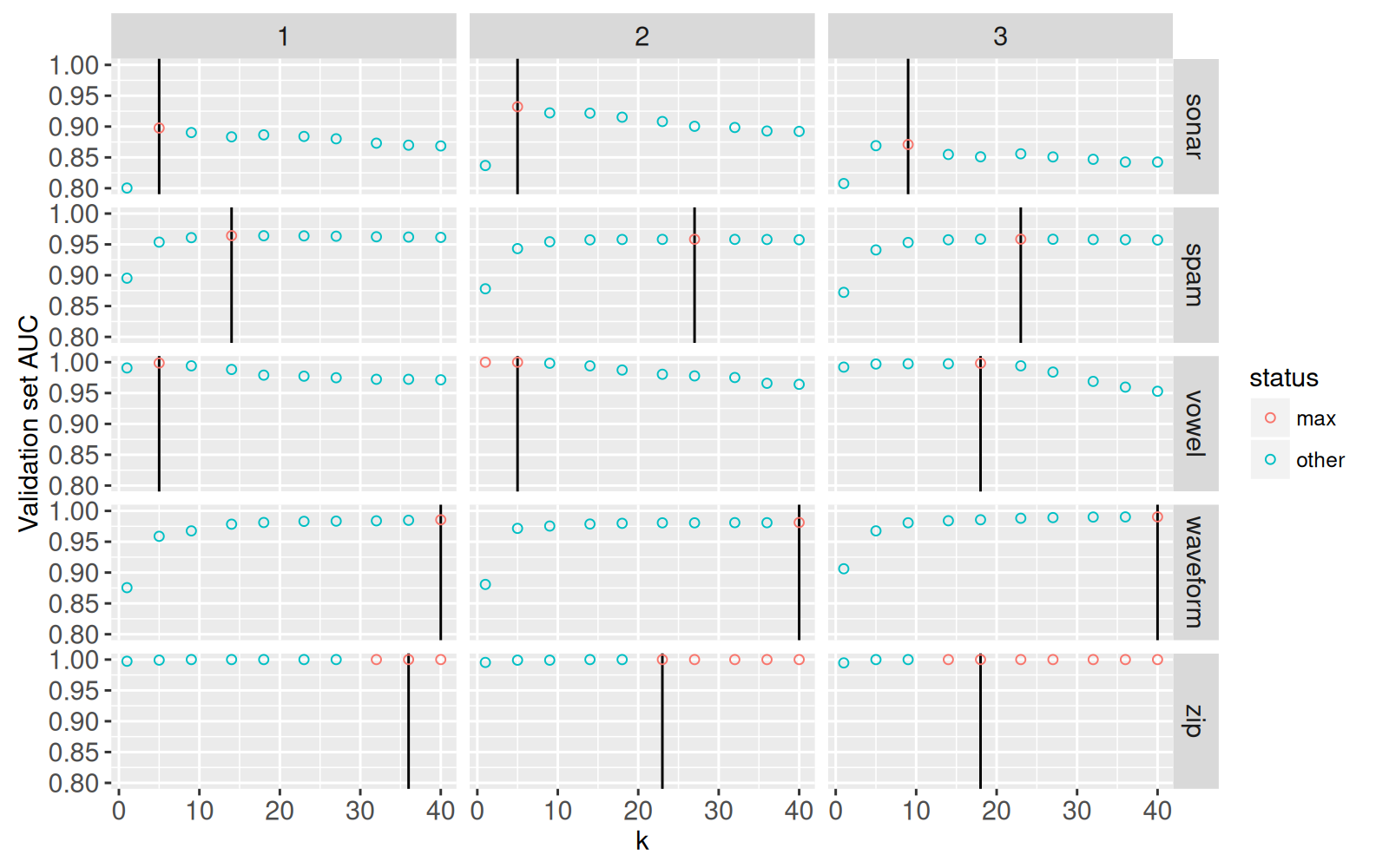

Dans le graphique ci-dessus, nous utilisons

• couleur pour souligner les meilleurs choix pour le nombre de voisins, et
• une ligne verticale pour indiquer le choix retenu.

Nous voyons que

• Pour trois jeux de données (sonar, spam, vowel) nous avons une AUC maximale avec un nombre de voisins intermédiare, ce qui indique un bon niveau de régularisation (ni surapprentissage, ni sous-apprentissage). Pour vowel itération 2, nous avons une AUC maximale avec seulement 1 voisin, soit le plus petit hyper-paramètre dans notre recherche. D’habitude, ça pourrait suggèrer qu’il vaut mieux élargir l’espace de recherche, en espèrant qu’un hyper-paramètre encore plus petit soit meilleur. Cependant, puisque 1 voisin est le plus petit nombre de voisins possible, il ne peut s’agir de sous-apprentissage; nous n’avons donc pas besoin d’élargir notre recherche dans ce cas-ci.
• Pour deux jeux de données (waveform, zip) nous avons une AUC maximale avec le plus grand nombre de voisins (40), ce qui suggère un surapprentissage. Ces résultats laissent supposer que nous pourrions éventuellement améliorer l’AUC en augmentant le nombre de voisins au-delà de 40. Idéalement, nous voyons l’AUC diminuer pour le nombre maximal de voisins, ce qui indique une recherche suffisamment élargie.

Nous créons ensuite une visualisation interactive pour comprendre le choix du nombre de voisins.

animint(
  testAUC=gg.auc+
    ggtitle("Select data set and cross-validation split"),
  knnDetails=gg.neighbors+
    ggtitle("Nearest neighbors model selection")+
    theme_animint(update_axes="y", last_in_row=TRUE))

Le graphique de gauche permet de sélectionner un jeu de données et une division de validation croisée. Si vous cliquez sur zip ou sur waveform, vous observerez une AUC maximale pour le plus grand nombre de voisins (40), ce qui suggère un surapprentissage. Exercice : refaites l’apprentissage en augmentant le max nombre de voisins. Est-ce vous voyez le max AUC avec un nombre de voisins intermédiaire ?

20.4.2 Torch

Dans cette section, nous explorons la régularisation d’arrêt prématuré, avec les algoritmes d’apprentissage dans le package torch. Ces algorithmes utilisent la descente de gradient, ce qui minimise une fonction de perte sur l’ensemble de sous-entraînement. Normalement la perte va aussi descendre sur l’ensemble de validation, jusqu’à un certain nombre d’époques, après quoi la perte va augmenter. Nous voulons arrêter la descente de gradient quand la perte est minimale sur l’ensemble de validation, ce qui est « prématuré » car la perte va toujours descendre sur l’ensemble de sous-entraînement. Nous allons vérifier que le nombre d’époques est choisi correctement, pour éviter le sous-apprentissage et le surapprentissage. Nous commençons avec le calcul d’une variable best_epoch, soit le nombre d’époques choisi (normalement le meilleur sur l’ensemble de validation).

score_torch <- score_dt[
  grepl("torch",learner_id)
][, best_epoch := sapply(
  learner, function(L)unlist(L$tuning_result$internal_tuned_values)
)]

Ensuite, nous créons un tableau représentant l’histoire d’entraînement, avec une ligne pour chaque époque.

(history_torch <- score_torch[, {
  L <- learner[[1]]
  M <- L$archive$learners(1)[[1]]$model
  M$torch_model_classif$model$callbacks$history
}, by=.(task_id, learner_id, iteration, task_it)])

      task_id     learner_id iteration task_it epoch train.classif.logloss
   1:    spam   torch_linear         1  spam 1     1          3.449127e-01
   2:    spam   torch_linear         1  spam 1     2          2.670158e-01
  ---                                                                     
5999:     zip torch_dense_50         3   zip 3   199          2.800170e-05
6000:     zip torch_dense_50         3   zip 3   200          2.784225e-05
      train.classif.auc valid.classif.logloss valid.classif.auc
   1:         0.9389462           0.281684344         0.9526053
   2:         0.9598620           0.261826903         0.9600733
  ---                                                          
5999:         1.0000000           0.001839860         1.0000000
6000:         1.0000000           0.001837298         1.0000000

Le tableau ci-dessus contient une ligne pour chaque époque, et les colonnes suivantes :

• train.classif.logloss, la perte logistique (entropie croisée) sur l’ensemble utilisé pour calculer les gradients, ce qui devrait toujours diminuer, si les hyper-paramètres sont appropriés (taux d’apprentissage, taille de lot, etc.). Remarquons que le nom train « entraînement » pourrait faire croire qu’il faudra encore diviser ces données en sous-entraînement et validation, mais ce n’est pas le cas. Pour préciser, nous allons plutôt utiliser le nom subtrain « sous-entraînement » dans les codes et les graphiques ci-dessous.
• valid.classif.logloss, la perte logistique (entropie croisée) sur l’ensemble qui n’est pas utilisé pour le calcul des gradients. Minimiser cette perte est le critère utilisé pour choisir le meilleur nombre d’époques, car classif.logloss était la première mesure dans measure_list.

Ensuite, nous créons un tableau mieux adapté à la visualisation.

(history_long <- nc::capture_melt_single(
  history_torch,
  set=nc::alevels(valid="validation", train="subtrain"),
  ".classif.",
  measure=nc::alevels("logloss", auc="AUC")))

       task_id     learner_id iteration task_it epoch        set measure
    1:    spam   torch_linear         1  spam 1     1   subtrain logloss
    2:    spam   torch_linear         1  spam 1     2   subtrain logloss
   ---                                                                  
23999:     zip torch_dense_50         3   zip 3   199 validation     AUC
24000:     zip torch_dense_50         3   zip 3   200 validation     AUC
           value
    1: 0.3449127
    2: 0.2670158
   ---          
23999: 1.0000000
24000: 1.0000000

Le tableau ci-dessus contient les nouvelles colonnes set, measure, and value. Nous utilisons le code ci-dessous pour la visualisation d’un sous-ensemble.

one_split <- function(DT,it=1)DT[iteration==it & task_id=="sonar"]
one_split_history <- one_split(history_long)
(gg.torch.line <- ggplot()+
  theme_bw()+
  facet_grid(measure ~ learner_id, labeller=label_both, scales="free")+
  geom_line(aes(
    epoch, value, color=set),
    data=one_split_history))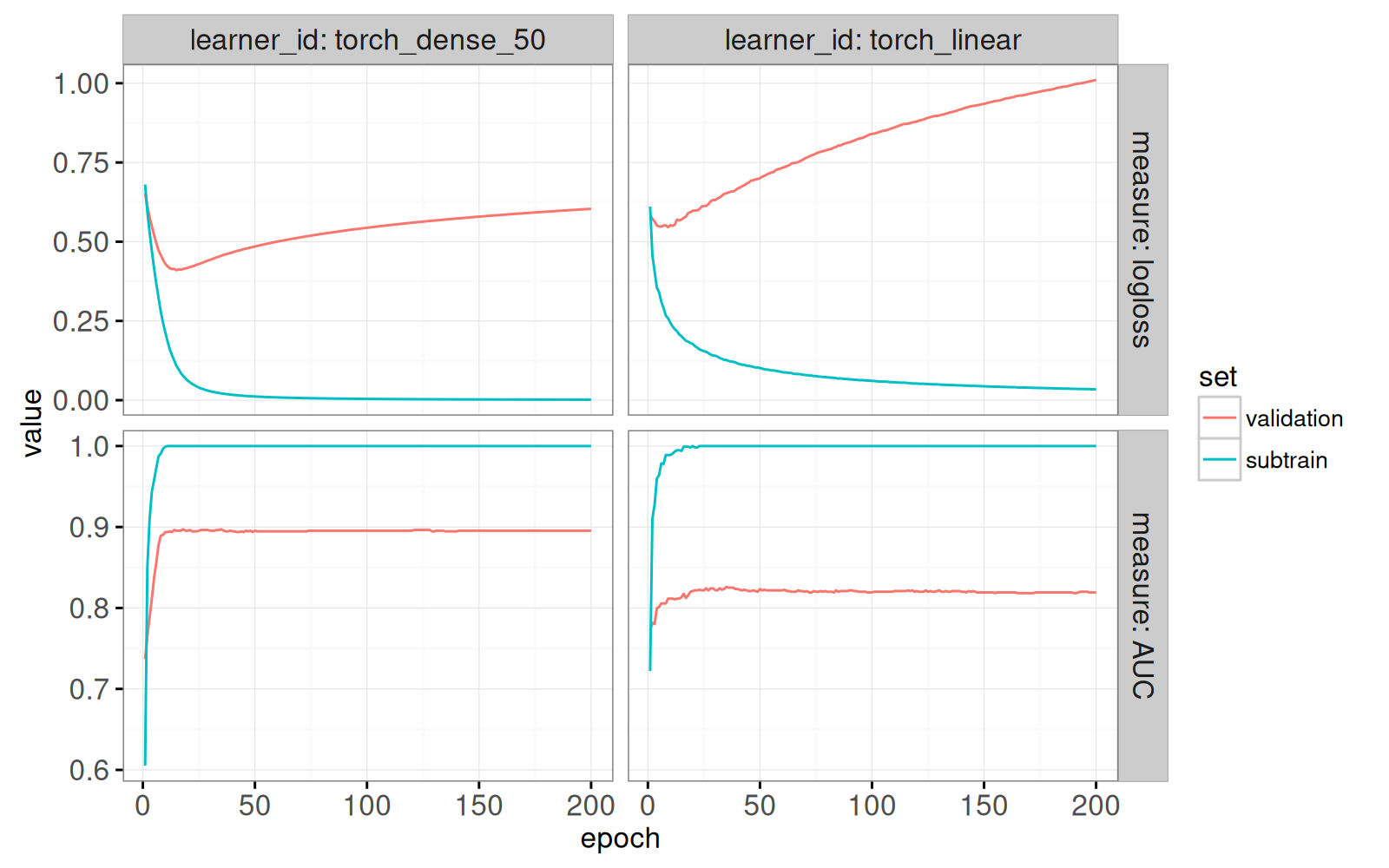

Le graphique ci-dessus contient des courbes d’apprentissage typiques.

• La perte logistique diminue, et l’AUC augmente, pour l’ensemble de sous-apprentissage (utilisé dans le calcul des gradients).
• Comme attendu, la perte sur l’ensemble de validation diminue en premier, pour ensuite remonter plus tard. Typiquement nous choissisons le nombre d’époques qui minimise cette courbe (ou bien, qui maximise l’AUC pous l’ensemble de validation).

Nous ajoutons maintenant des points pour mettre en évidence le minimum et le maximum.

history_best <- history_long[, {
  mfun <- if(measure=="AUC")max else min
  .SD[value==mfun(value)]
}, by=.(task_id, iteration, task_it, learner_id, measure, set)
][, point := "best"]
one_split_best <- one_split(history_best)
(gg.torch.point <- gg.torch.line+
  geom_point(aes(
    epoch, value, color=set, fill=point),
    data=one_split_best)+
   scale_fill_manual(values=c(best="black")))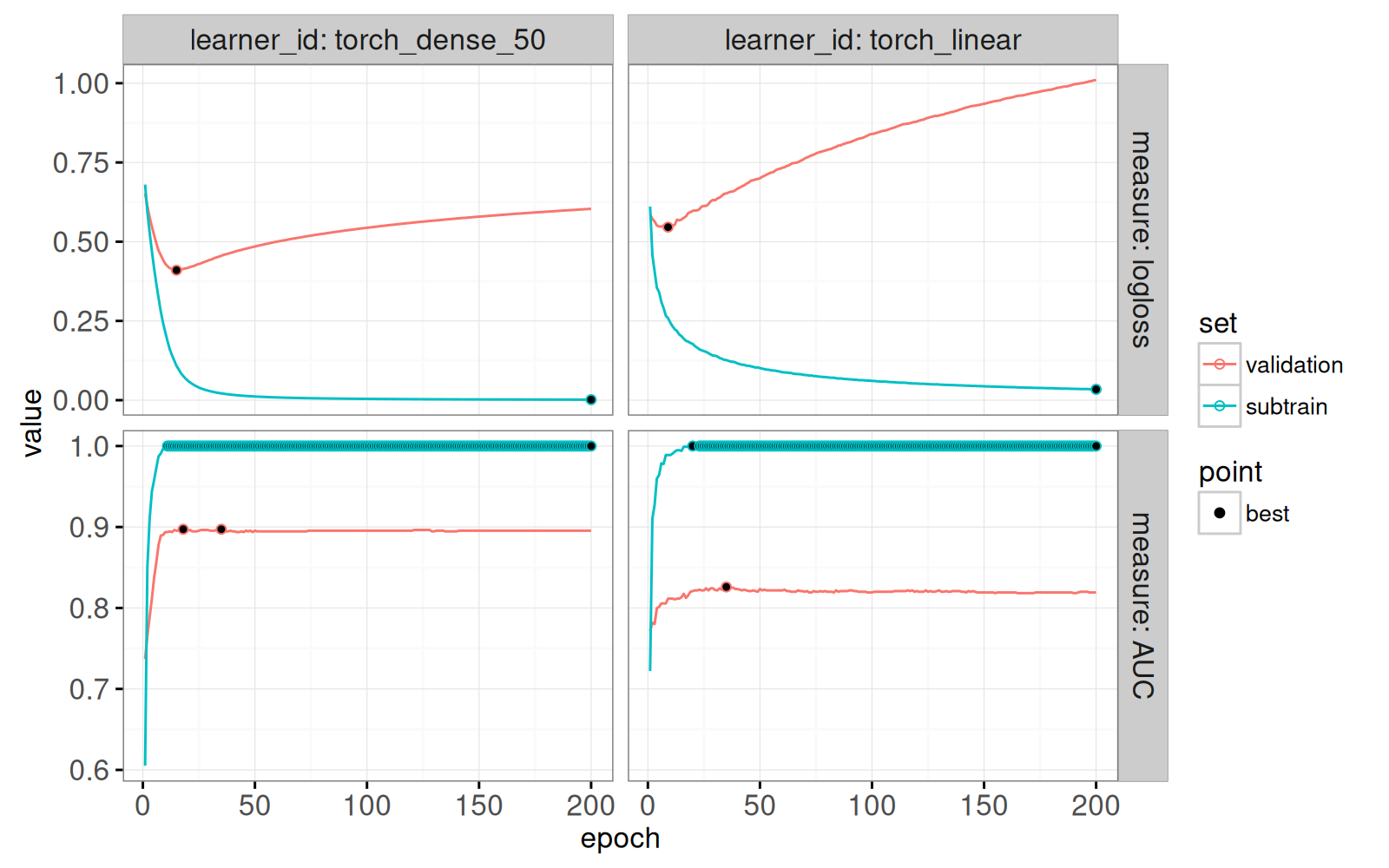

Le graphique ci-dessus révèle des caractéristiques importantes :

• il n’y a qu’un minimum pour chaque courbe de perte logistique;
• il peut y avoir plus du’un maximum d’AUC;
• pour l’ensemble de sous-entraînement, l’AUC atteint rapidement le maximum (1), mais la perte logistique continue de diminuer.

Nous rajoutons ensuite des lignes verticales pour mettre en évidence le nombre d’époques choisi.

one_split_score <- one_split(score_torch)
(gg.torch.text <- gg.torch.point+
  geom_vline(aes(
    xintercept=best_epoch),
    data=one_split_score)+
  geom_text(aes(
    best_epoch, -Inf, label=paste0(" selected epoch=", best_epoch)),
    vjust=-0.5, hjust=0,
    data=one_split_score))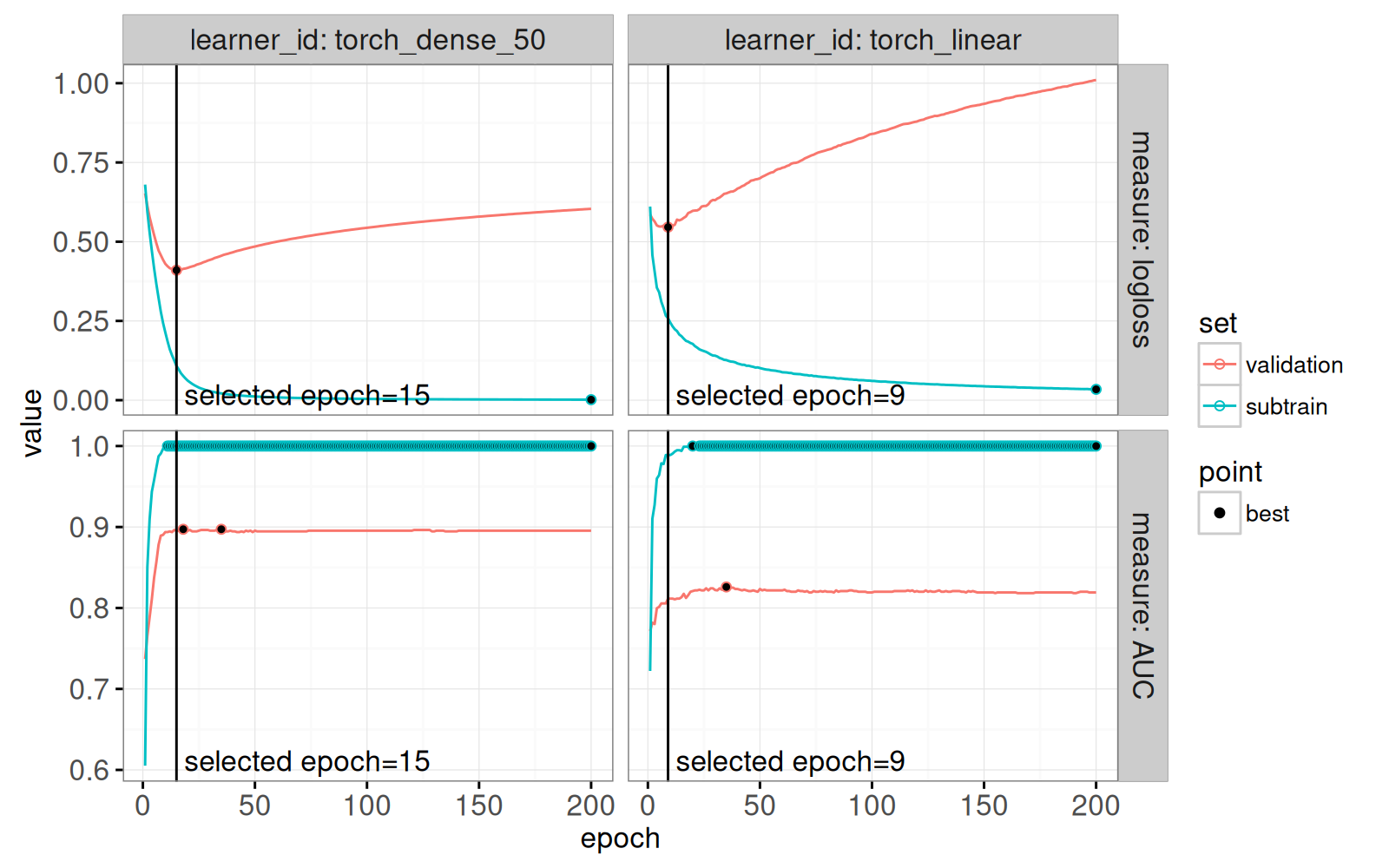

Ci-dessus nous voyons que nous avons choisi le nombre d’époques qui minimise la perte logistique sur l’ensemble de validation. Ensuite, nous proposons un résumé, qui affiche le nombre d’époques pour chaque jeu de données, division de validation croisée et algorithme d’apprentissage.

(history_best_wide <- dcast(
  history_best,
  learner_id + set + task_id + iteration + task_it ~ measure,
  list(min, max, mid=function(x)(min(x)+max(x))/2),
  value.var="epoch"))

        learner_id        set task_id iteration task_it epoch_min_logloss
 1: torch_dense_50 validation   sonar         1 sonar 1                15
 2: torch_dense_50 validation   sonar         2 sonar 2                 9
---                                                                      
59:   torch_linear   subtrain     zip         2   zip 2               200
60:   torch_linear   subtrain     zip         3   zip 3               200
    epoch_min_AUC epoch_max_logloss epoch_max_AUC epoch_mid_logloss
 1:            18                15            35                15
 2:             2                 9             2                 9
---                                                                
59:             2               200           200               200
60:             2               200           200               200
    epoch_mid_AUC
 1:          26.5
 2:           2.0
---              
59:         101.0
60:         101.0

Le tableau présente des colonnes pour les époques correspondant aux meilleures mesures. Dans le graphique ci-dessous, nous utilisons les valeurs mid, soit à mi-chemin.

history_best_valid <- history_best_wide[set=="validation"]
learner.colors <- c(
  torch_linear="grey",
  torch_dense_50="red")
(gg.best.valid <- ggplot()+
   theme_bw()+
   scale_fill_manual(values=learner.colors)+
   xlab("Epochs with best validation log loss")+
   ylab("Epochs with best validation AUC")+
   geom_point(aes(
     epoch_mid_logloss, epoch_mid_AUC, fill=learner_id),
     clickSelects="task_it", size=5,
     color_off="white", color="black",
     data=history_best_valid)+
   facet_wrap("task_id"))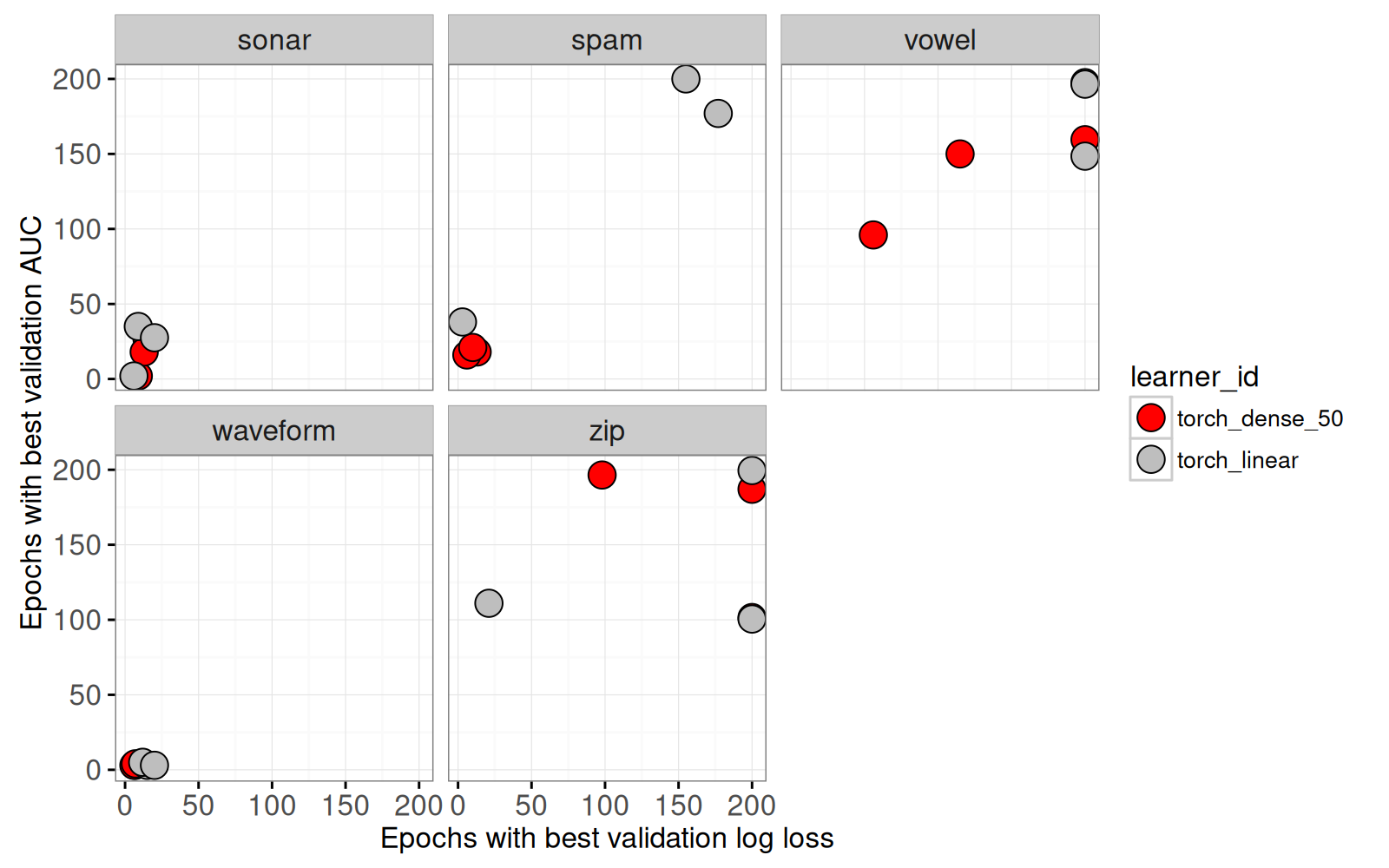

Dans le graphique ci-dessus, il est clair que

• pour certains jeux de données (sonar and waveform), la meilleure époque a des valeurs inférieures au maximum. Ces résultats suggèrent que le choix pour le nombre d’époques est bon (ni surapprentissage ni sous-apprentissage).
• pour d’autres jeux de données (vowel and zip) la meilleure époque correspond au maximum (200 époques). Ces résultats suggèrent un sous-apprentissage (nous pouvons augmenter le nombre d’époques pour minimiser davantage la perte sur l’ensemble de validation).

Ensuite nous rajoutons un segment pour afficher le min et max du nombre d’époques qui atteignent la meilleure AUC pour l’ensemble de validation.

(gg.best.seg <- gg.best.valid+
   scale_color_manual(values=learner.colors)+
   geom_segment(aes(
     epoch_mid_logloss, epoch_min_AUC,
     xend=epoch_mid_logloss, yend=epoch_max_AUC,
     color=learner_id),
     size=3,
     clickSelects="task_it",
     data=history_best_valid))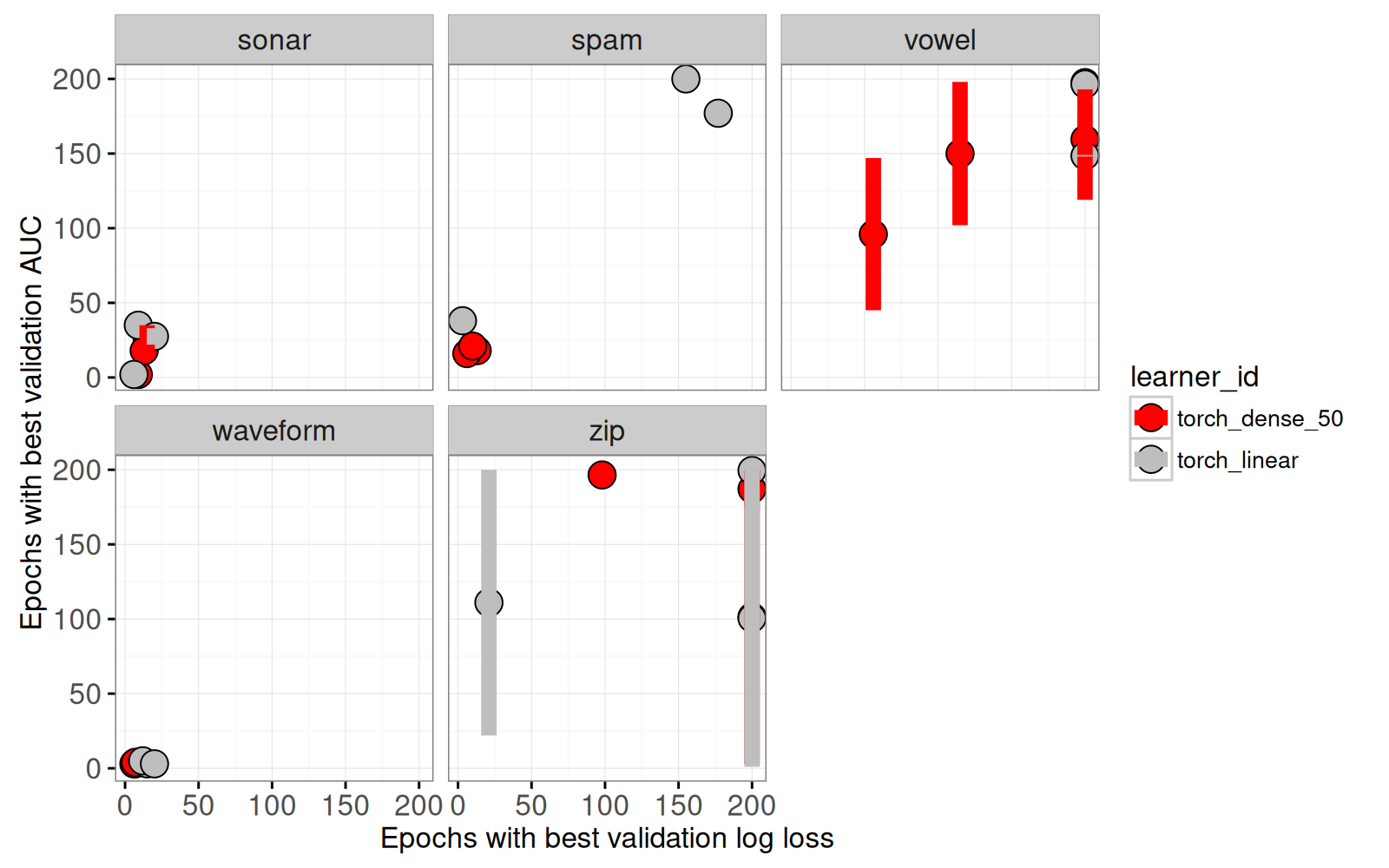

Ci-dessus nous voyons qu’il y a plusieurs époques qui atteignent le maximum d’AUC, dans les ensembles validation de vowel et zip. Nous préparons ensuite un graphique pour afficher les détails, avec des valeurs relatives entre 0 et 1 (car les valeurs absolues sont très différentes d’un jeu de données à l’autre).

norm01 <- function(x)(x-min(x))/(max(x)-min(x))
history_long[
, relative_values := norm01(value)
, by=.(iteration, task_id, learner_id, set, measure)]
gg.log.auc <- ggplot()+
   theme_bw()+
   facet_grid(measure ~ learner_id, scales="free")+
   scale_x_continuous(breaks=seq(50,200,by=50))+
   geom_line(aes(
     epoch, relative_values, color=set, group=set),
     showSelected="task_it",
     data=history_long)

Enfin, nous combinons les graphiques pour créer une visualisation interactive.

(viz.torch <- animint(
  overview=gg.best.seg+
    theme_animint(width=800, colspan=2, last_in_row=TRUE)+
    ggtitle("Select task and cross-validation iteration"),
  details=gg.log.auc+
    ggtitle("Selected learning curves")))

Ci-dessous nous voyons deux graphiques :

• Cliquez sur le graphique du haut pour sélectionner un jeu de données et une division de validation croisée.
• Le graphique du bas affichera les courbes d’apprentissage pour la sélection.

Pour certains jeux de données, l’AUC atteint rapidement un maximum proche de 1, ce qui rend difficile d’observer à quel point la courbe se rapproche de 1. Pour visualiser ces détails, nous calculons l’inverse de l’AUC (1-AUC). La meilleure valeur de l’AUC est 1, mais la meilleure valeur pour l’inverse de l’AUC est 0. Nous pouvons alors utiliser l’échelle logarithmique pour visualiser à quel point la courbe est proche de 0.

history_long[, let(
  Measure = factor(
    ifelse(measure=="logloss", "logloss", "InvAUC"),
    c("logloss","InvAUC")),
  Relative_values = ifelse(
    measure=="logloss", relative_values, 1-relative_values))]
gg.log.scale <- ggplot()+
   theme_bw()+
   facet_grid(Measure ~ learner_id, scales="free")+
   scale_x_continuous(breaks=seq(50,200,by=50))+
   scale_y_log10()+
   geom_line(aes(
     epoch, Relative_values, color=set, group=set),
     showSelected=c("task_it", "set"),
     data=history_long)

Remarquons que dans le code ci-dessus que nous avons utilisé des majuscules pour les variables Measure et Relative_values, et une échelle logarithmique pour Y. Nous ajoutons ensuite ce graphique à la visualisation interactive.

viz.torch.log <- viz.torch
viz.torch.log$detailsLog <- gg.log.scale+
  ggtitle("Selected learning curves (log scale)")+
  theme(legend.position="none")
viz.torch.log

La visualisation contient un graphique en bas à droite, qui affiche l’échelle logarithmique pour la sélection. En cliquant sur vowel, nous voyons des différences entre les graphiques de détails (en bas à droite, nous voyons mieux quelles époques sont les meilleures).

20.4.3 glmnet

Dans cette section, nous explorons des visualisations de l’algorithme de glmnet, un modèle linéaire avec régularisation L1. Nous commençons avec la méthode plot() du premier modèle.

score_glmnet <- score_dt[grep("glmnet",learner_id)]
L <- score_glmnet$learner[[1]]
library(glmnet)

Loading required package: Matrix

Loaded glmnet 4.1-10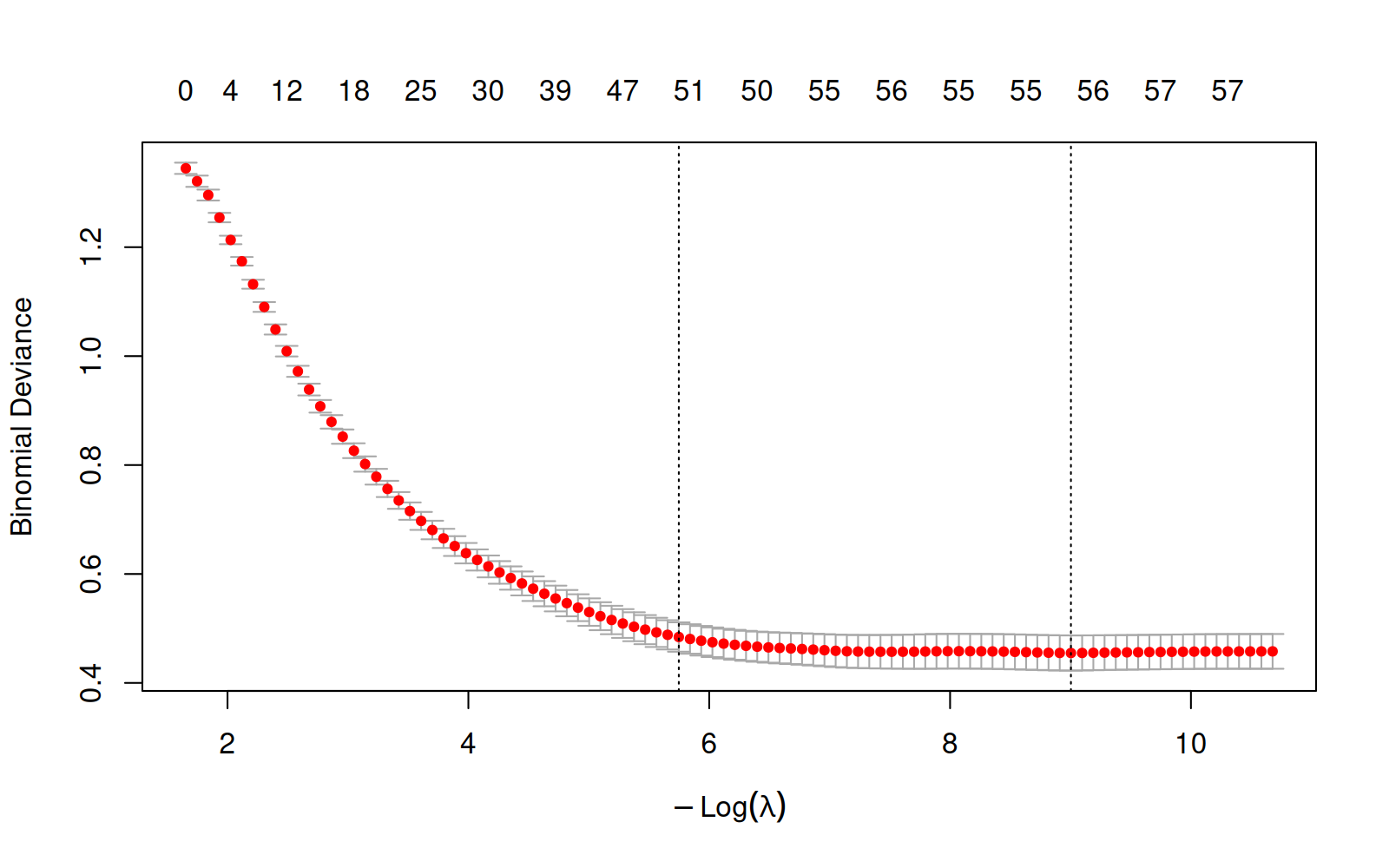

plot(L$model)
score_glmnet[1, title(paste(task_id, iteration), line=3)]

NULL

Dans le graphique ci-dessus, nous voyons la perte logistique « Binomial Deviance » pour l’ensemble de validation, en fonction de la taille du modèle (nombre de non-zéro coefficients en haut, négative log pénalité en bas). Nous voyons une courbe qui descend, mais qui ne remonte pas, ce qui suggère un sous-apprentissage. Nous faisons une version de ce graphique avec le code ci-dessous.

cv_glmnet_one <- with(L$model, data.table(nzero, lambda, cvm, cvsd))
(gg.glmnet <- ggplot()+
   scale_y_continuous("Validation log loss")+
   geom_segment(aes(
     -log(lambda), cvm+cvsd,
     xend=-log(lambda), yend=cvm-cvsd),
     data=cv_glmnet_one)+
   geom_point(aes(
     -log(lambda), cvm, fill=nzero),
     data=cv_glmnet_one)+
   scale_fill_gradient(low="white", high="red"))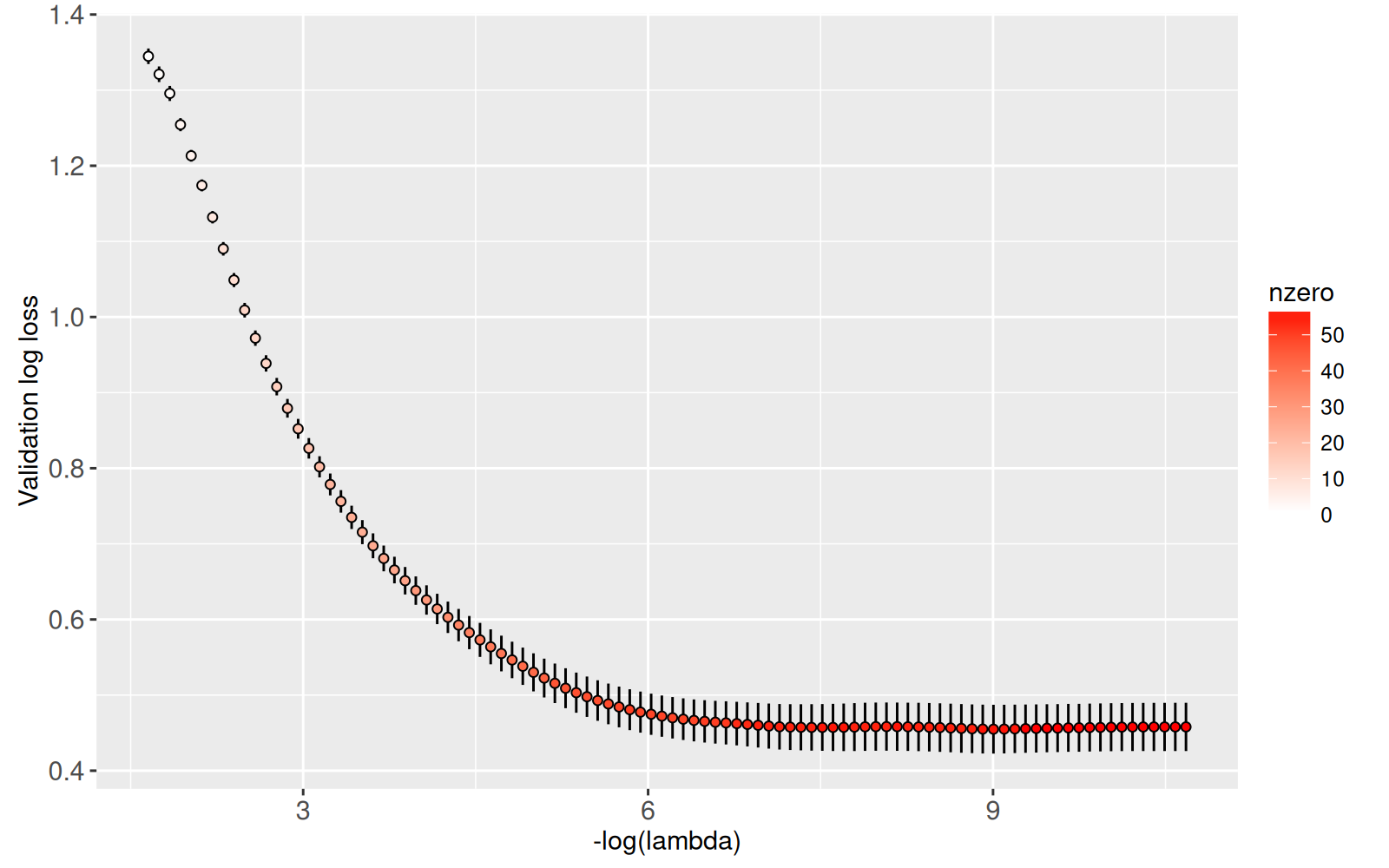

Ci-dessus nous voyons un ggplot qui ressemble au graphique précédant, avec la couleur indiquant le nombre de non-zéro coefficients. Ensuite, nous rajoutons du texte pour souligner le nombre de non-zéro coefficients pour plusieurs niveaux de régularisation.

gg.glmnet+
  geom_text(aes(
    -log(lambda), Inf, label=nzero),
    vjust=1,
    data=cv_glmnet_one[seq(1, .N, by=5)])

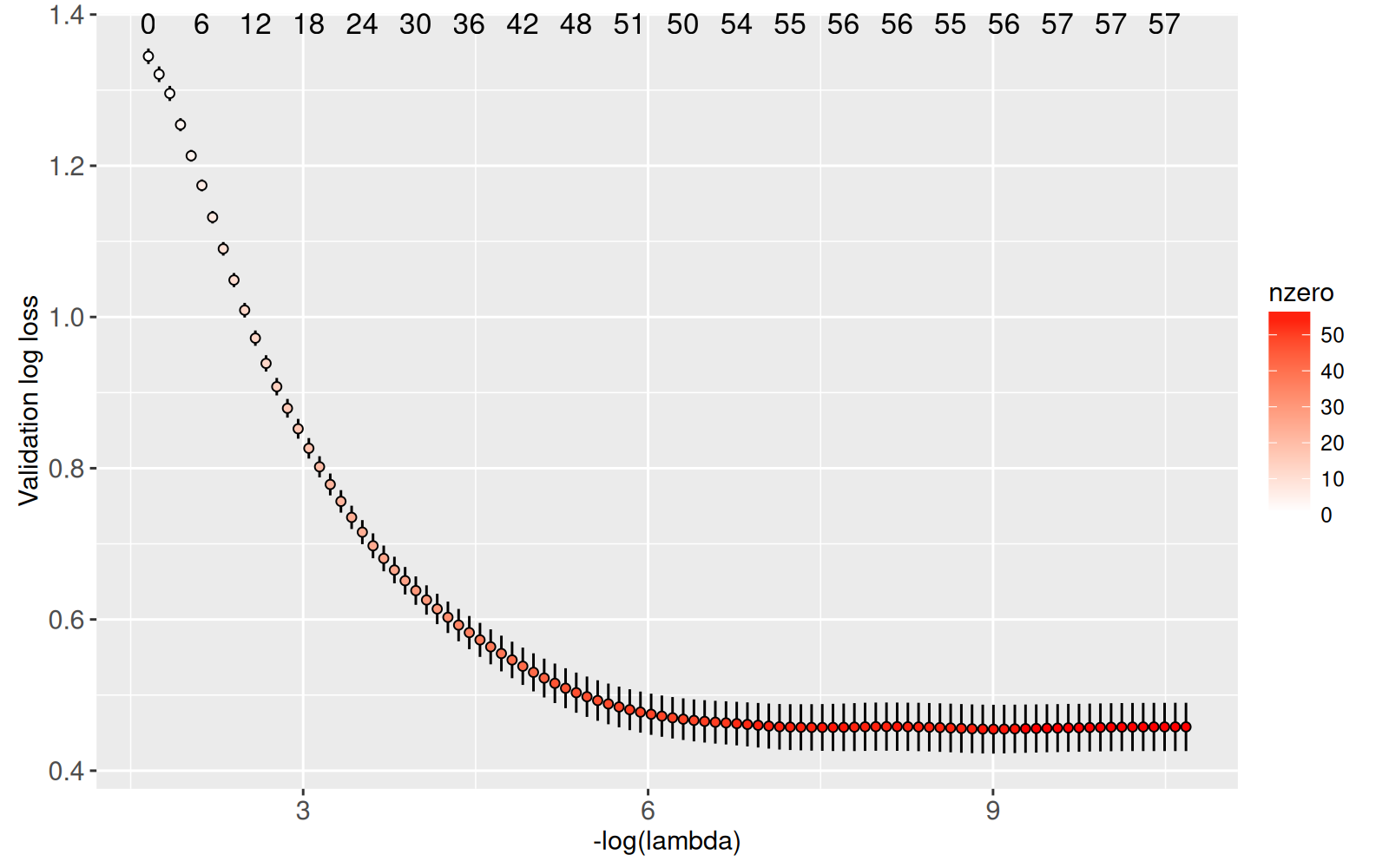
Le graphique ci-dessus affiche le nombre de non-zéro coefficients en haut, pour plusieurs niveaux de régularisation. Notre but dans cette section est de faire une visualisation interactive avec ces informations. Dans le code ci-dessous, nous calculons un tableau de résultats pour tous les modèles.

(cv_glmnet_all <- score_glmnet[, with(learner[[1]]$model, data.table(
  nzero, lambda, cvm, cvsd
)), by=.(task_id, iteration, task_it)])

      task_id iteration task_it nzero       lambda         cvm        cvsd
   1:    spam         1  spam 1     0 0.1913004906 1.344799861 0.010327734
   2:    spam         1  spam 1     1 0.1743058823 1.321052558 0.010319197
  ---                                                                     
1401:     zip         3   zip 3    48 0.0002196736 0.008797191 0.002780171
1402:     zip         3   zip 3    48 0.0002001584 0.008481994 0.002723400

Le tableau ci-dessus contient une ligne pour chaque jeu de données, chaque division de validation croisée et chaque niveau de régularisation. Ensuite nous affichons la perte logistique sur l’ensemble de validation, avec une courbe pour chaque division de validation croisée et un panneau pour chaque jeu de données.

ggplot()+
  scale_y_continuous("Validation log loss")+
  geom_line(aes(
    -log(lambda), cvm, group=iteration),
    data=cv_glmnet_all)+
  facet_wrap("task_id", scales="free")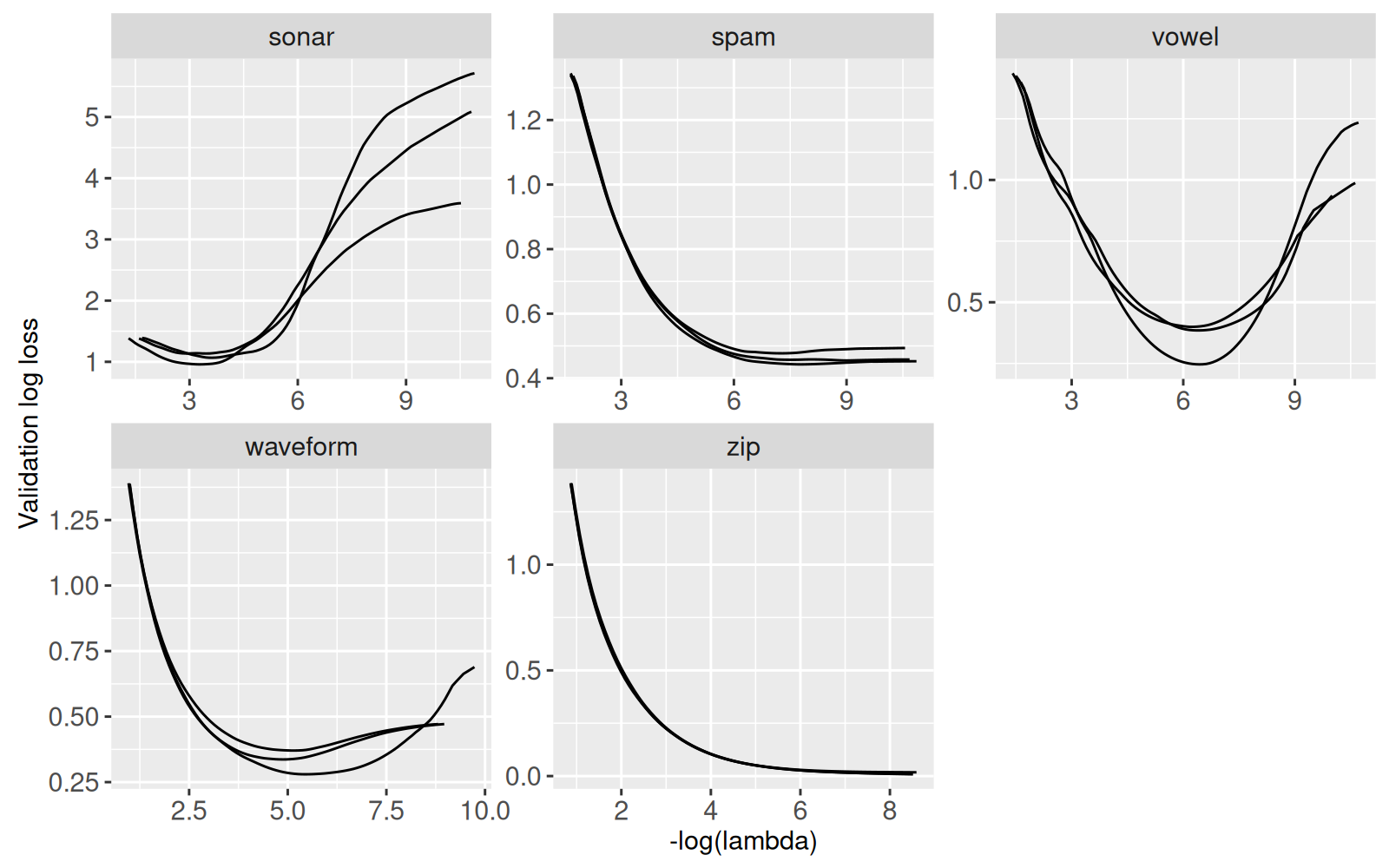

Ci-dessus nous voyons que le modèle lineaire risque le surapprentissage dans trois jeux de données (sonar, vowel, waveform), si le niveau de régularisation est trop faible. Dans les autres jeux de données (spam and zip), nous voyons une courbe qui ne remonte pas, ce qui suggère le sous-apprentissage. Nous pourrions donc soupçonner qu’un modèle non-linéaire serait capable de donner des meilleurs résultats. En regardant les résultats précédents, nous pourrions vérifier cette hypothèse.

• Dans spam, nous voyons que torch_dense_50 obtient de meilleurs résultats que cv_glmnet. Nous en déduisons qu’une fonction linéaire n’est pas assez puissante pour obtenir la prédiction optimale dans ces données.
• Dans zip, nous voyons que tous les algorithmes d’apprentissage donnent une fonction de prédiction parfaite (ou presque). Nous en déduisons que ces données réprésentent un problème de prédiction qui est très facile pour tous les algorithmes (même le modèle linéaire).

20.5 Résumé du chapitre et exercices

Nous avons créé plusieurs visualisations des résultats d’apprentissage de mlr3.

Exercices :

• Dans viz.select.fpr, il n’y a pas de transitions fluides. Rajoutez-en une pour la variable FPR, et définissez aes(key) pour geom_point() et geom_text() dans gg.tpr.
• Dans viz.select.fpr, un graphique affiche le meilleur taux de vrais positifs pour la sélection du taux de faux positifs. Enlevez ce graphique, et rajoutez les mêmes informations avec geom_point() et geom_label_aligned() dans le graphique avec les courbes ROC.
• Le graphique gg.summary affiche seulement le max AUC. Rajoutez un geom_segment() qui affiche la variation d’AUC entre les algorithmes.
• Le graphique viz.select.fpr affiche le meilleur taux de vrais positifs pour la sélection du taux de faux positifs.
  • Rajoutez un graphique « Meilleur taux d’erreur pour la sélection du taux de faux positifs ». Indice : pour calculer le taux d’erreur, il faut faire une jointure entre le nombre d’étiquettes et les courbes ROC.
  • Rajoutez un geom_text() qui affiche le taux séléctionné de faux positifs.
  • Faites une visualisation qui affiche le meilleur taux de faux positifs, pour une sélection du taux de vrais positifs.
• Dans les légendes, les deux modèles linéaires (cv_glmnet et torch_linear) ont différentes couleurs (jaune et violet). Accordez les deux couleurs (par exemple, violet pâle et violet foncé).
• Dans les visualisations des courbes ROC, rajoutez aes(color) ou aes(fill) aux autres graphiques, avec une légende cohérente avec les courbes ROC. Affichez seulement une légende, avec les éléments triés pour accorder à l’ordre de présentation des axes Y affichant learner_id. Assurez-vous que vous pouvez cliquer sur un élément de la légende pour faire disparaître toutes les données correspondantes à cet algorithme d’apprentissage, à travers tous les graphiques.
• Dans viz.torch.log, rajoutez des points pour mettre en évidence les meilleures époques, et une ligne verticale pour indiquer l’époque choisie par la validation croisée.
• Chaque section du chapitre a présenté sa propre méthode de visualisation. Combinez plusieurs méthodes dans une seule visualisation :
  • Affichez les trois graphiques pour la vérification de la régularisation (glmnet, torch, nearest neighbors).
  • Affichez les courbes ROC interactives à côté des graphiques pour la vérification de la régularisation.

Ensuite, l’annexe explique certaines méthodes de programmation R qui sont généralement utiles pour la visualisation de données.

Bischl, Bernd, Raphael Sonabend, Lars Kotthoff, et Michel Lang, éd. 2024. Applied Machine Learning Using mlr3 in R. CRC Press. https://mlr3book.mlr-org.com.

Hastie, Trevor, Robert Tibshirani, et Jerome Friedman. 2009. The elements of statistical learning. Second. Springer Series in Statistics. Springer Science+Business Media, LLC, 233 Spring Street, New York NY 10013, USA: Springer. https://hastie.su.domains/ElemStatLearn/.

Hocking, Toby. 2025. « Comparing neural network architectures using mlr3torch ».