# K-moyennes
<!-- paragraph -->
```{r setup, echo=FALSE}
knitr::opts_chunk$set(fig.path="ch17-figures/")
```
<!-- paragraph -->
Dans ce chapitre, nous allons explorer plusieurs visualisations de l'agrégation (clustering) par K-moyennes, un algorithme d'apprentissage non supervisé.
<!-- paragraph -->
Plan du chapitre :
<!-- paragraph -->
- Nous commençons par visualiser deux caractéristiques des données Iris.
<!-- comment -->
- Nous choisissons de manière aléatoire K=trois points de données à utiliser comme centres d'agrégation.
<!-- comment -->
- Nous expliquons comment calculer et visualiser la distance entre les points de données et les centres d'agrégation.
<!-- comment -->
- Nous terminons par une visualisation de l'évolution des paramètres du modèle K-moyennes à chaque itération.
<!-- paragraph -->
## Visualisation des données de l'iris avec des étiquettes {#viz-iris}
<!-- paragraph -->
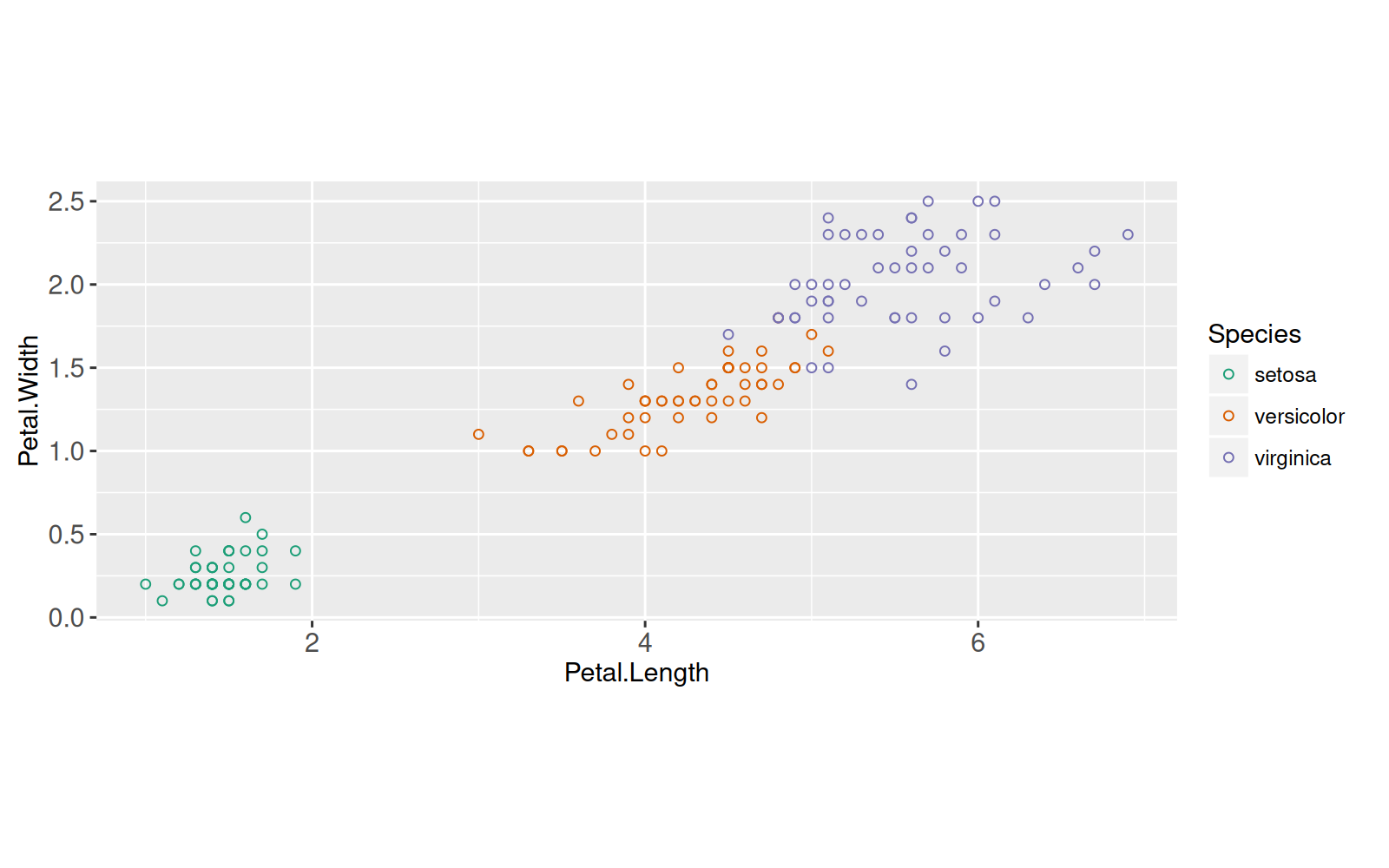
Nous commençons par une visualisation typique des données de l'iris, comprenant une légende de couleurs pour indiquer les Espèces.
<!-- paragraph -->
```{r}
library(animint2)
color.code <- c(
setosa="#1B9E77",
versicolor="#D95F02",
virginica="#7570B3",
"1"="#E7298A",
"2"="#66A61E",
"3"="#E6AB02",
"4"="#A6761D")
ggplot()+
scale_color_manual(values=color.code)+
geom_point(aes(
Petal.Length, Petal.Width, color=Species),
data=iris)+
coord_equal()
```
<!-- paragraph -->
Nous allons illustrer l'algorithme d'agrégation K-moyennes à l'aide de ces deux dimensions.
<!-- paragraph -->
```{r, results=TRUE}
data.mat <- as.matrix(iris[,c("Petal.Width","Petal.Length")])
head(data.mat)
str(data.mat)
```
<!-- paragraph -->
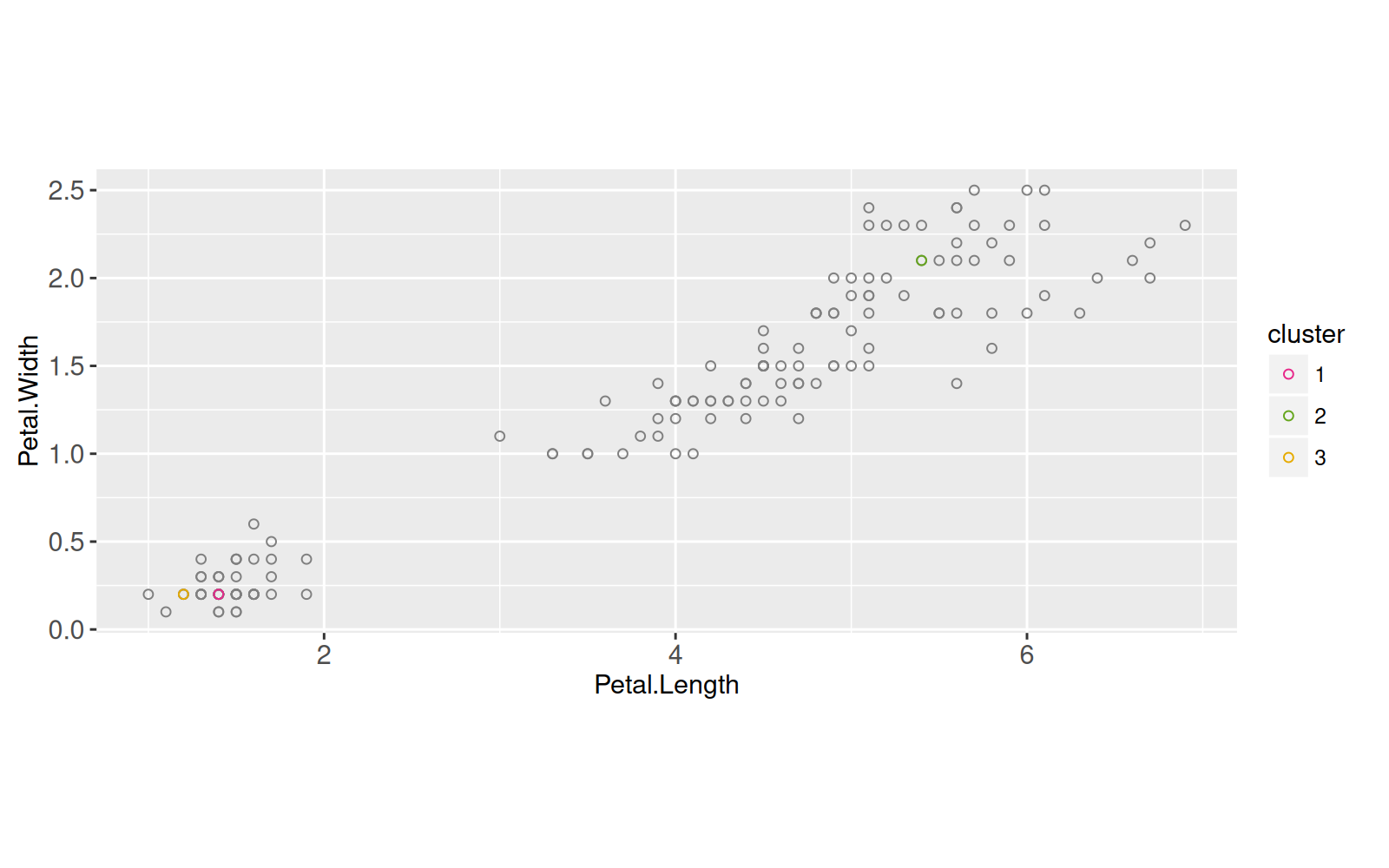
Pour exécuter K-moyennes, l'hyperparamètre du nombre d'agrégations (K) doit être fixé à l'avance.
<!-- comment -->
Ensuite, les K-points de données aléatoires sont sélectionnés comme centres d'agrégation initiaux,
<!-- paragraph -->
```{r}
K <- 3
library(data.table)
data.dt <- data.table(data.mat)
set.seed(3)
centers.dt <- data.dt[sample(1:.N, K)]
(centers.mat <- as.matrix(centers.dt))
centers.dt[, cluster := factor(1:K)]
centers.dt
gg.centers <- ggplot()+
scale_color_manual(values=color.code)+
geom_point(aes(
Petal.Length, Petal.Width),
color="grey50",
data=data.dt)+
geom_point(aes(
Petal.Length, Petal.Width, color=cluster),
data=centers.dt)+
coord_equal()
gg.centers
```
<!-- paragraph -->
Ci-dessus, nous avons affiché les deux ensembles de données (centres d'agrégation et données) à l'aide de deux instances de `geom_point()`.
<!-- comment -->
Nous calculons ci-dessous la distance entre chaque point de données et chaque centre d'agrégation,
<!-- paragraph -->
```{r}
pairs.dt <- data.table(expand.grid(
centers.i=1:nrow(centers.mat),
data.i=1:nrow(data.mat)))
```
<!-- paragraph -->
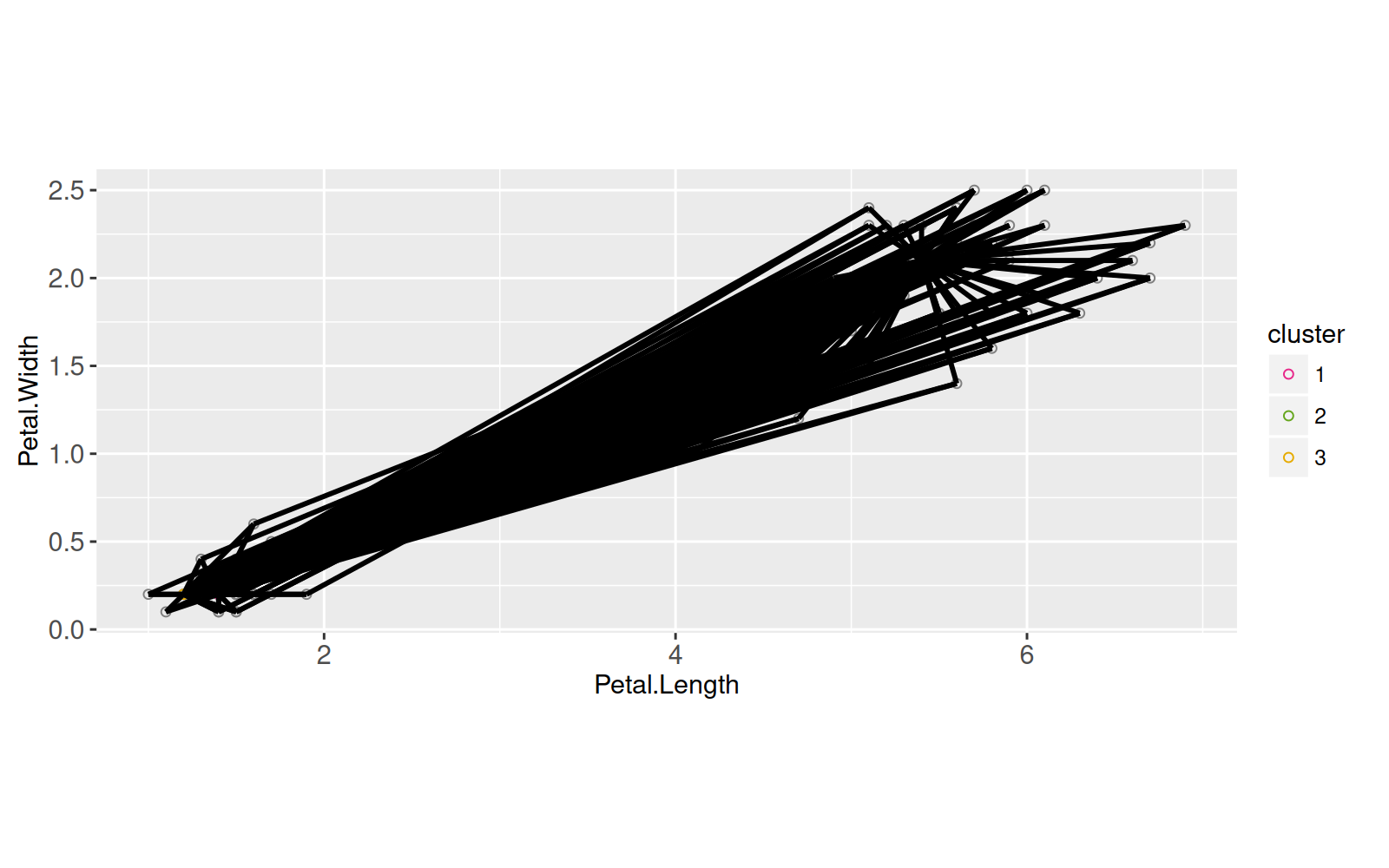
Ces éléments peuvent être visualisés à l'aide d'un `geom_point()`,
<!-- paragraph -->
```{r}
seg.dt <- pairs.dt[, data.table(
data.i,
data=data.mat[data.i,],
center=centers.mat[centers.i,])]
gg.centers+
geom_segment(aes(
data.Petal.Length, data.Petal.Width,
xend=center.Petal.Length, yend=center.Petal.Width),
size=1,
data=seg.dt)
```
<!-- paragraph -->
Il y a `r nrow(seg.dt)` segments superposés ci-dessus, de sorte que l'interactivité serait utile pour mettre en évidence les segments connectés à un point de données précis.
<!-- comment -->
Pour ce faire, nous créons une variable de sélection `data.i`,
<!-- paragraph -->
```{r ch17-kmeans-distances}
animint(
ggplot()+
theme_bw()+
theme_animint(height=300, width=640)+
scale_color_manual(values=color.code)+
scale_x_continuous(breaks=seq(1,7,by=0.5))+
scale_y_continuous(breaks=seq(0, 2.5, by=0.5))+
geom_point(aes(
Petal.Length, Petal.Width, color=cluster),
size=4,
data=centers.dt)+
geom_segment(aes(
data.Petal.Length, data.Petal.Width,
xend=center.Petal.Length, yend=center.Petal.Width),
size=1,
showSelected="data.i",
data=seg.dt)+
geom_point(aes(
Petal.Length, Petal.Width),
clickSelects="data.i",
size=2,
color="grey50",
data=data.table(data.mat, data.i=1:nrow(data.mat))))
```
<!-- paragraph -->
Dans la visualisation des données ci-dessus, vous pouvez cliquer sur un point de données pour afficher les distances entre ce point et chaque centre d'agrégation.
<!-- paragraph -->
Exercices pour cette section :
<!-- paragraph -->
- Modifier les échelles x/y de façon à ce que les mêmes tics soient représentés.
<!-- comment -->
- Modifier la couleur de chaque segment pour qu'elle soit la même que l'agrégation correspondante.
<!-- comment -->
- Ajouter une infobulle qui indique la valeur de la distance.
<!-- comment -->
- Faire varier la largeur du segment en fonction de son optimalité (le segment connecté au centre de l'agrégation la plus proche devrait être mis en évidence par une largeur plus élevée).
<!-- paragraph -->
## Visualisation des itérations de l'algorithme {#viz-iterations}
<!-- paragraph -->
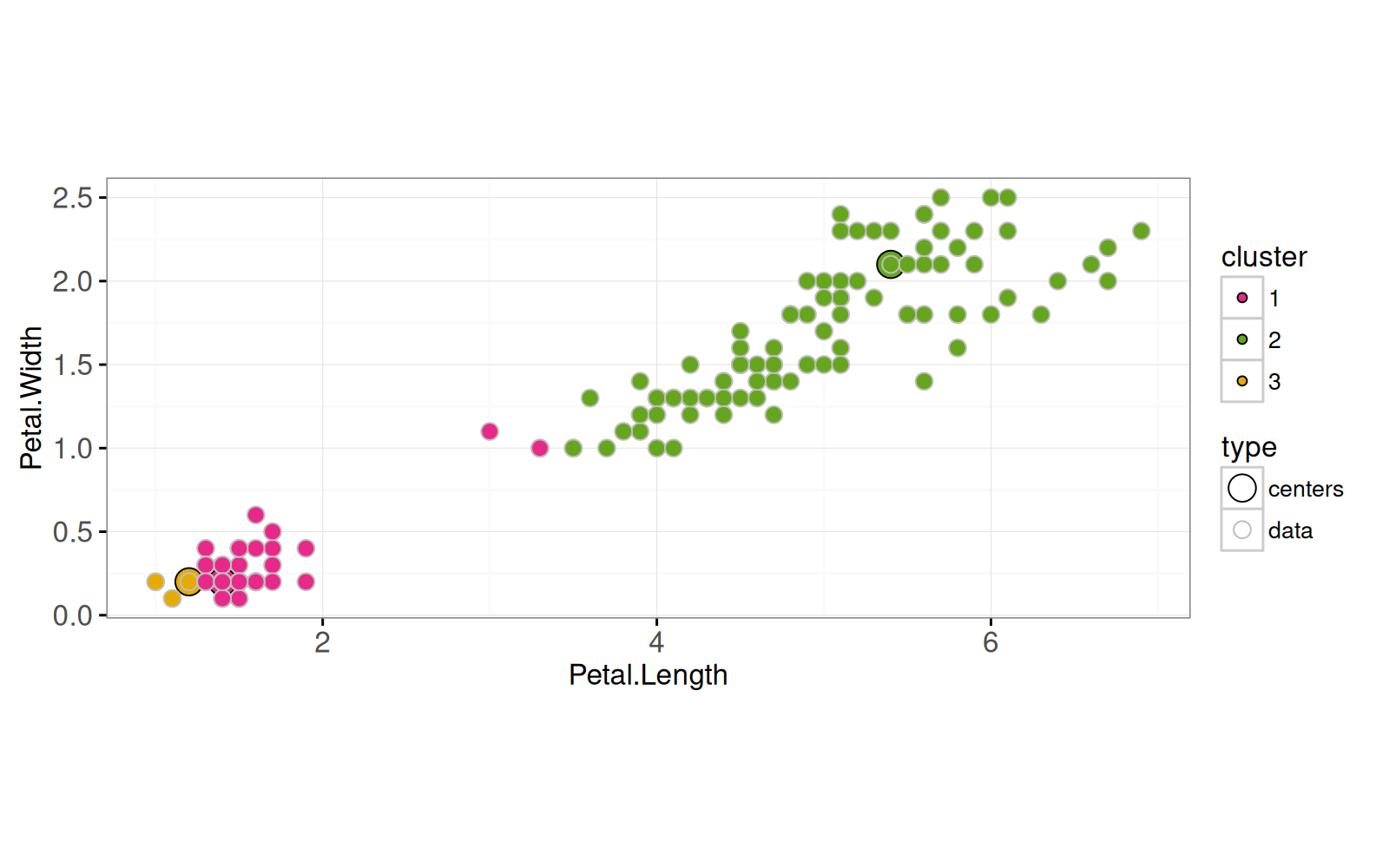
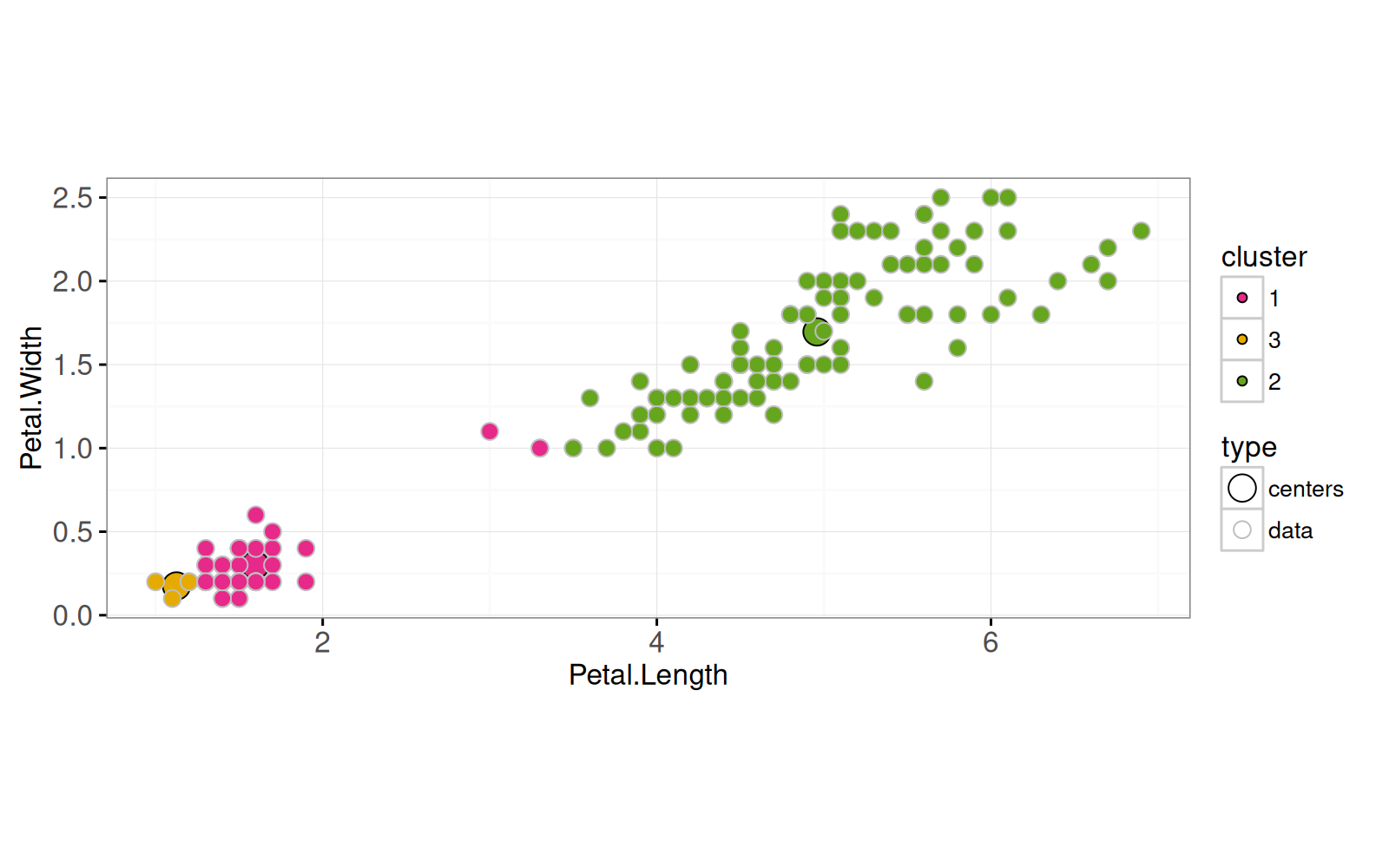
Nous calculons le centre d'agrégation le plus proche pour chaque point de données,
<!-- paragraph -->
```{r}
pairs.dt[, error := rowSums(
(data.mat[data.i,]-centers.mat[centers.i,])^2)]
(closest.dt <- pairs.dt[, .SD[which.min(error)], by=data.i])
(closest.data <- closest.dt[, .(
data.dt[data.i],
cluster=factor(centers.i)
)])
(both.dt <- rbind(
data.table(type="centers", centers.dt),
data.table(type="data", closest.data)))
ggplot()+
scale_fill_manual(values=color.code)+
scale_color_manual(values=c(centers="black", data="grey"))+
scale_size_manual(values=c(centers=5, data=3))+
geom_point(aes(
Petal.Length, Petal.Width, fill=cluster, size=type, color=type),
data=both.dt)+
coord_equal()+
theme_bw()
```
<!-- paragraph -->
Ensuite, nous mettons à jour les centres d'agrégation,
<!-- paragraph -->
```{r}
new.centers <- closest.dt[, data.table(
t(colMeans(data.dt[data.i]))
), by=.(cluster=centers.i)]
(new.both <- rbind(
data.table(type="centers", new.centers),
data.table(type="data", closest.data)))
ggplot()+
scale_fill_manual(values=color.code)+
scale_color_manual(values=c(centers="black", data="grey"))+
scale_size_manual(values=c(centers=5, data=3))+
geom_point(aes(
Petal.Length, Petal.Width, fill=cluster, size=type, color=type),
data=new.both)+
coord_equal()+
theme_bw()
```
<!-- paragraph -->
Les visualisations ci-dessus montrent donc les étapes de la méthode K-moyennes : (1) mise à jour de l'agrégation sur la base du centre le plus proche (2) mise à jour du centre sur la base des données affectées à cette agrégation.
<!-- comment -->
Pour visualiser plusieurs itérations des deux étapes ci-dessus, nous pouvons utiliser une boucle for,
<!-- paragraph -->
```{r}
set.seed(3)
centers.dt <- data.dt[sample(1:.N, K)]
(centers.mat <- as.matrix(centers.dt))
data.and.centers.list <- list()
iteration.error.list <- list()
for(iteration in 1:20){
pairs.dt[, error := {
rowSums((data.mat[data.i,]-centers.mat[centers.i,])^2)
}]
closest.dt <- pairs.dt[, .SD[which.min(error)], by=data.i]
iteration.error.list[[iteration]] <- data.table(
iteration, error=sum(closest.dt[["error"]]))
iteration.both <- rbind(
data.table(type="centers", centers.dt, cluster=1:K),
closest.dt[, data.table(
type="data", data.dt[data.i], cluster=factor(centers.i))])
data.and.centers.list[[iteration]] <- data.table(
iteration, iteration.both)
new.centers <- closest.dt[, data.table(
t(colMeans(data.dt[data.i]))
), keyby=.(cluster=centers.i)]
centers.dt <- new.centers[, names(centers.dt), with=FALSE]
centers.mat <- as.matrix(centers.dt)
}
(data.and.centers <- do.call(rbind, data.and.centers.list))
(iteration.error <- do.call(rbind, iteration.error.list))
```
<!-- paragraph -->
Nous commençons par créer un graphique d'ensemble avec une courbe d'erreur qui servira à sélectionner la taille du modèle,
<!-- paragraph -->
```{r}
gg.err <- ggplot()+
theme_bw()+
geom_point(aes(
iteration, error),
data=iteration.error)+
make_tallrect(iteration.error, "iteration", alpha=0.3)
```
<!-- paragraph -->
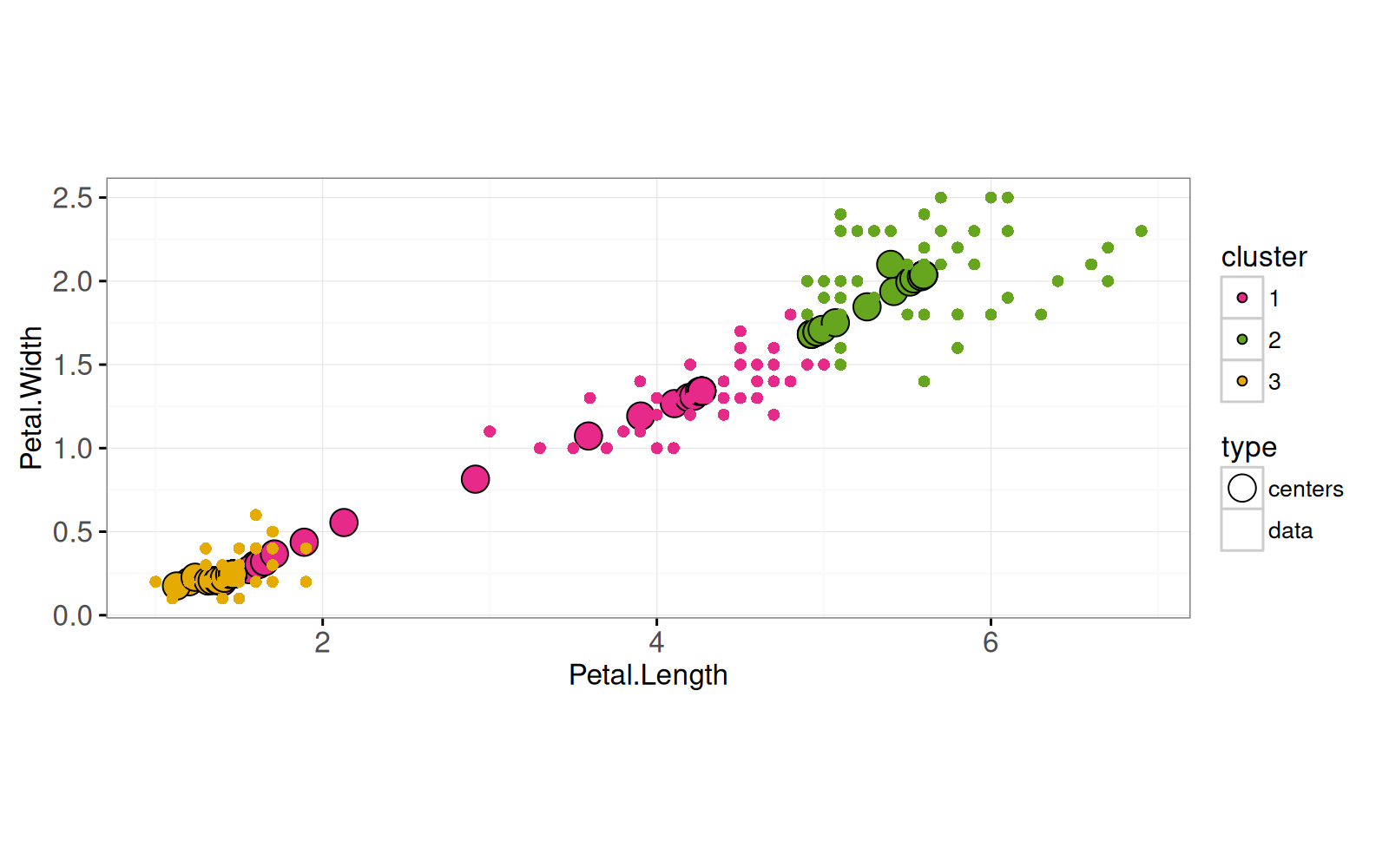
Nous créons également un graphique qui indique l'itération en cours,
<!-- paragraph -->
```{r}
gg.iteration <- ggplot()+
scale_fill_manual(values=color.code)+
scale_color_manual(values=c(centers="black", data=NA))+
scale_size_manual(values=c(centers=5, data=2))+
geom_point(aes(
Petal.Length, Petal.Width, fill=cluster, size=type, color=type),
showSelected="iteration",
data=data.and.centers)+
coord_equal()+
theme_bw()
gg.iteration
```
<!-- paragraph -->
La combinaison des deux graphiques permet d'obtenir une visualisation des données interactive,
<!-- paragraph -->
```{r ch17-kmeans-iterations}
animint(gg.err, gg.iteration)
```
<!-- paragraph -->
## Résumé du chapitre et exercices {#ch17-exercises}
<!-- paragraph -->
Exercices :
<!-- paragraph -->
- Faites en sorte que les centres apparaissent toujours au premier plan (au-dessus des données).
<!-- comment -->
- Ajoutez des transitions en douceur.
<!-- comment -->
- Ajoutez une animation sur la variable d'itération.
<!-- comment -->
- Le code actuel impose un nombre maximum d'itérations, il est donc possible que les dernières ne progressent pas.
<!-- comment -->
Par exemple, dans l'image ci-dessus, l'itération 16 est la dernière à réduire l'erreur (les itérations 17 à 20 n'entraînent aucune diminution).
<!-- comment -->
Modifiez le code pour qu'il arrête l'itération s'il n'y a pas de diminution de l'erreur.
<!-- comment -->
- La visualisation actuelle n'a qu'un seul cadre d'animation (sous-ensemble `showSelected`) par itération (la moyenne est affichée avant sa mise à jour).
<!-- comment -->
Ajoutez un autre cadre d'animation qui montre la moyenne après la mise à jour.
<!-- comment -->
- Ajoutez des segments interactifs qui montrent la distance entre chaque point de données et chaque centre d'agrégation (comme dans le premier animint de cette page).
<!-- comment -->
- Ajoutez les fonctionnalités décrites dans les exercices de la section précédente.
<!-- comment -->
- Calculez les résultats pour différentes graines aléatoires, puis affichez les taux d'erreur correspondants sur le graphique d'aperçu des erreurs. Permettez ensuite à l'utilisateur de sélectionner n'importe lequel de ces résultats.
<!-- comment -->
- Calculez les résultats pour plusieurs nombres d'agrégations (K).
<!-- comment -->
Calculez l'indice de Rand ajusté en utilisant `pdfCluster::adj.rand.index(species, cluster)` pour chaque K et graine aléatoire différents.
<!-- comment -->
Ajoutez un graphique d'ensemble qui montre la valeur ARI de chaque modèle et autorise la sélection du nombre d'agrégations.
<!-- comment -->
- Effectuez une visualisation similaire en utilisant un autre ensemble de données tel que `data("penguins", package="palmerpenguins")`.
<!-- paragraph -->
Ensuite, dans le [chapitre 18](/ch18), nous vous expliquerons comment visualiser l'algorithme d'apprentissage par descente de gradient pour l'apprentissage des réseaux neuronaux.
<!-- paragraph -->