# Méthode de Newton pour la recherche de racines
<!-- paragraph -->
```{r setup, echo=FALSE}
knitr::opts_chunk$set(fig.path="Ch15-figures/")
```
<!-- paragraph -->
Les racines d'une fonction `f(x)` sont les valeurs de `x` telles que `f(x)=0`.
<!-- comment -->
Certaines fonctions `f` ont une expression explicite pour leurs racines.
<!-- comment -->
Par exemple :
<!-- paragraph -->
- la fonction linéaire `f(x)=b*x+c=0` a une seule racine `x=-c/b` lorsque b n'est pas nul.
<!-- comment -->
- la fonction quadratique `f(x)=a*x^2+b*x+c=0` a deux racines `x=(-b±sqrt(b^2-4*a*c))/(2*a)` si le discriminant est positif `b^2-4*a*c>0`.
<!-- comment -->
- la fonction sin `f(x)=sin(a*x)=0` a un nombre infini de racines : `pi*z/a` pour tous les entiers `z`.
<!-- paragraph -->
Cependant, certaines fonctions n'ont pas d'expression explicite pour leurs racines.
<!-- comment -->
Par exemple, les racines de la perte de Poisson `f(x)=a*x+b*log(x)+c` n'ont pas d'expression explicite comme on l'entend en termes de fonctions mathématiques courantes
<!-- comment -->
(en fait, il y a une solution faisant appel à la [fonction W de Lambert](https://www.wolframalpha.com/input/?i=a*x+%2Bb*log%28x%29%2B+c%3D0) mais cette fonction n'est généralement pas disponible). L'objectif de ce chapitre est de créer une visualisation des données interactive qui explique [la méthode de Newton](https://en.wikipedia.org/wiki/Newton%27s_method) pour trouver les racines de telles fonctions.
<!-- paragraph -->
Plan du chapitre :
<!-- paragraph -->
- Nous implémentons d'abord la méthode de Newton pour la perte de Poisson, afin de trouver la racine qui est plus grande que le minimum.
<!-- comment -->
Nous créons plusieurs visualisations de données statiques et une visualisation interactive.
<!-- comment -->
- Nous proposons ensuite un exercice pour trouver la racine qui est plus petite que le minimum.
<!-- paragraph -->
## Plus grande racine dans l'espace moyen {#larger-root}
<!-- paragraph -->
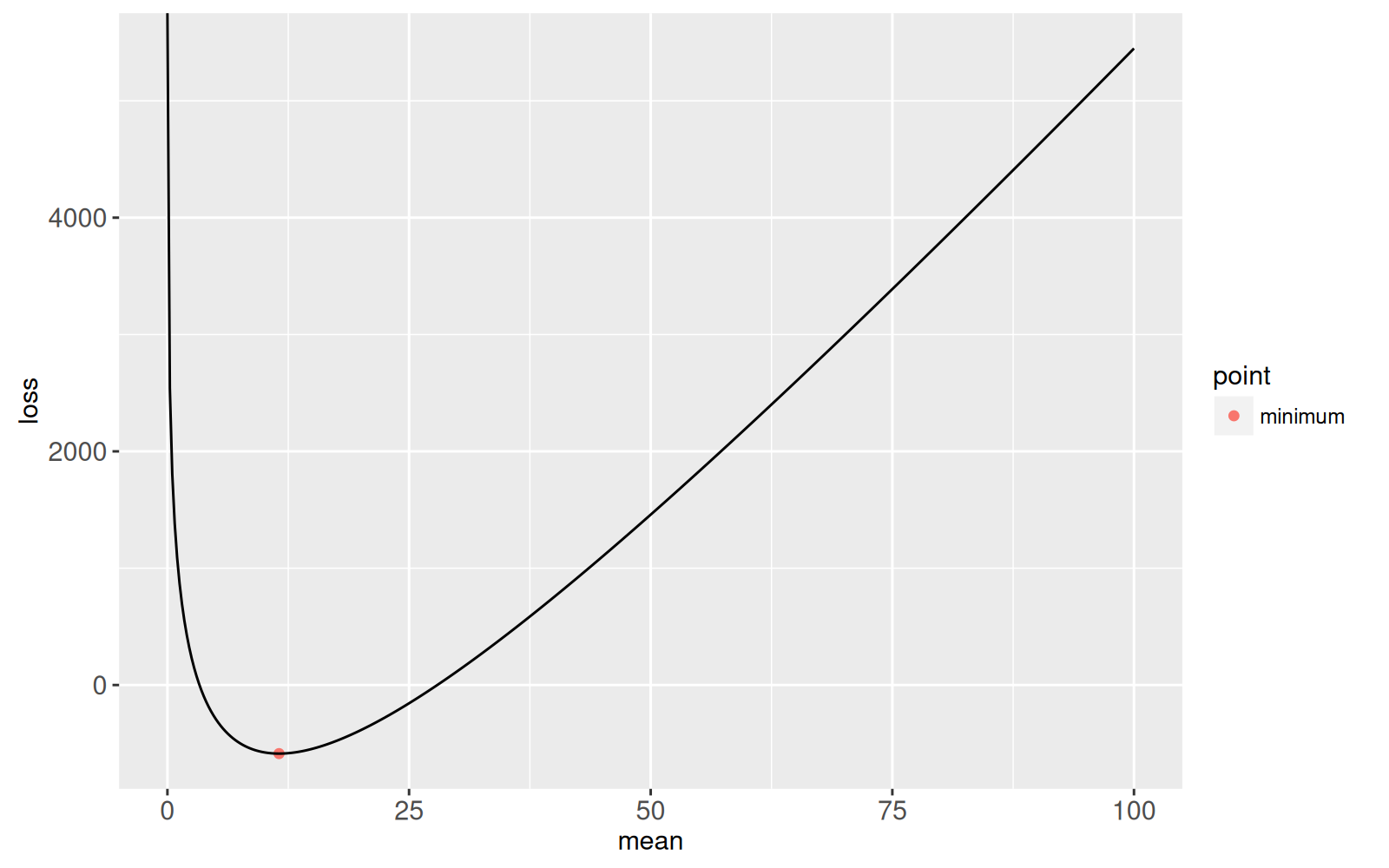
Nous commençons par définir les coefficients d'une fonction de perte de Poisson à deux racines.
<!-- paragraph -->
```{r}
Linear <- 95
Log <- -1097
Constant <- 1000
loss.fun <- function(Mean){
Linear*Mean + Log*log(Mean) + Constant
}
(mean.at.optimum <- -Log/Linear)
(loss.at.optimum <- loss.fun(mean.at.optimum))
library(data.table)
loss.dt <- data.table(mean=seq(0, 100, l=400))
loss.dt[, loss := loss.fun(mean)]
opt.dt <- data.table(
mean=mean.at.optimum,
loss=loss.at.optimum,
point="minimum")
library(animint2)
gg.loss <- ggplot()+
geom_point(aes(mean, loss, color=point), data=opt.dt)+
geom_line(aes(mean, loss), data=loss.dt)
print(gg.loss)
```
<!-- paragraph -->
Notre but est de trouver les deux racines de cette fonction.
<!-- comment -->
La méthode de Newton pour la recherche de racines prend comme point de départ une racine candidate choisie arbitrairement, puis utilise de manière itérative des approximations linéaires pour trouver des racines candidates plus précises.
<!-- comment -->
Pour calculer l'approximation linéaire, nous avons besoin de la dérivée :
<!-- paragraph -->
```{r}
loss.deriv <- function(Mean){
Linear + Log/Mean
}
```
<!-- paragraph -->
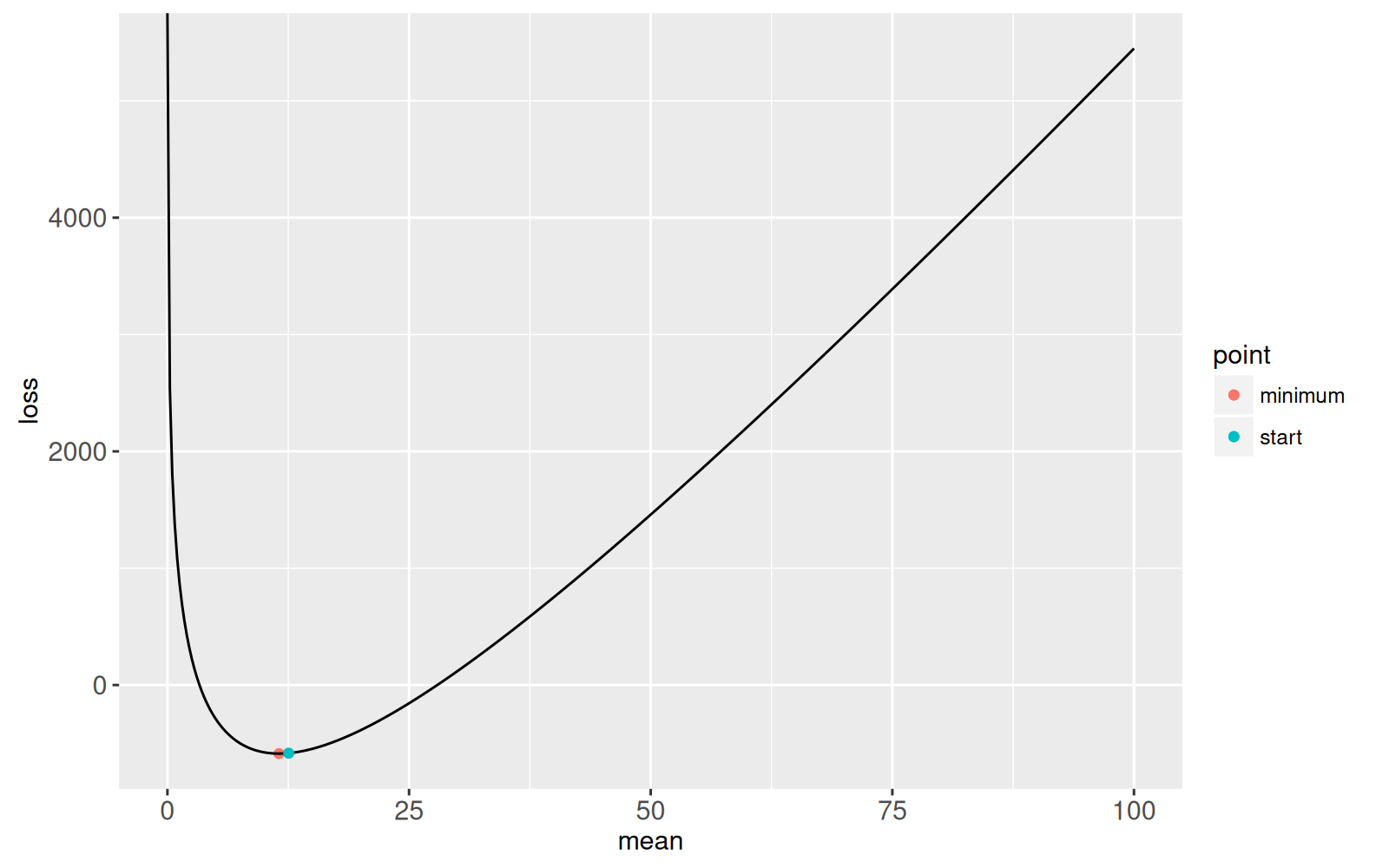
Nous commençons la recherche de la racine à un point plus grand que le minimum:
<!-- paragraph -->
```{r}
possible.root <- mean.at.optimum+1
gg.loss+
geom_point(aes(
mean, loss, color=point),
data=data.table(
point="start",
mean=possible.root,
loss=loss.fun(possible.root)))
```
<!-- paragraph -->
Nous utilisons ensuite l'implémentation suivante de la méthode de Newton pour trouver une racine:
<!-- paragraph -->
```{r}
iteration <- 1
solution.list <- list()
thresh.dt <- data.table(thresh=1e-6)
while(thresh.dt$thresh < abs({
fun.value <- loss.fun(possible.root)
})){
cat(sprintf("mean=%e loss=%e\n", possible.root, fun.value))
deriv.value <- loss.deriv(possible.root)
new.root <- possible.root - fun.value/deriv.value
solution.list[[iteration]] <- data.table(
iteration, possible.root, fun.value, deriv.value, new.root)
iteration <- iteration+1
possible.root <- new.root
}
root.dt <- data.table(point="root", possible.root, fun.value)
gg.loss+
geom_point(aes(possible.root, fun.value, color=point),
data=root.dt)
```
<!-- paragraph -->
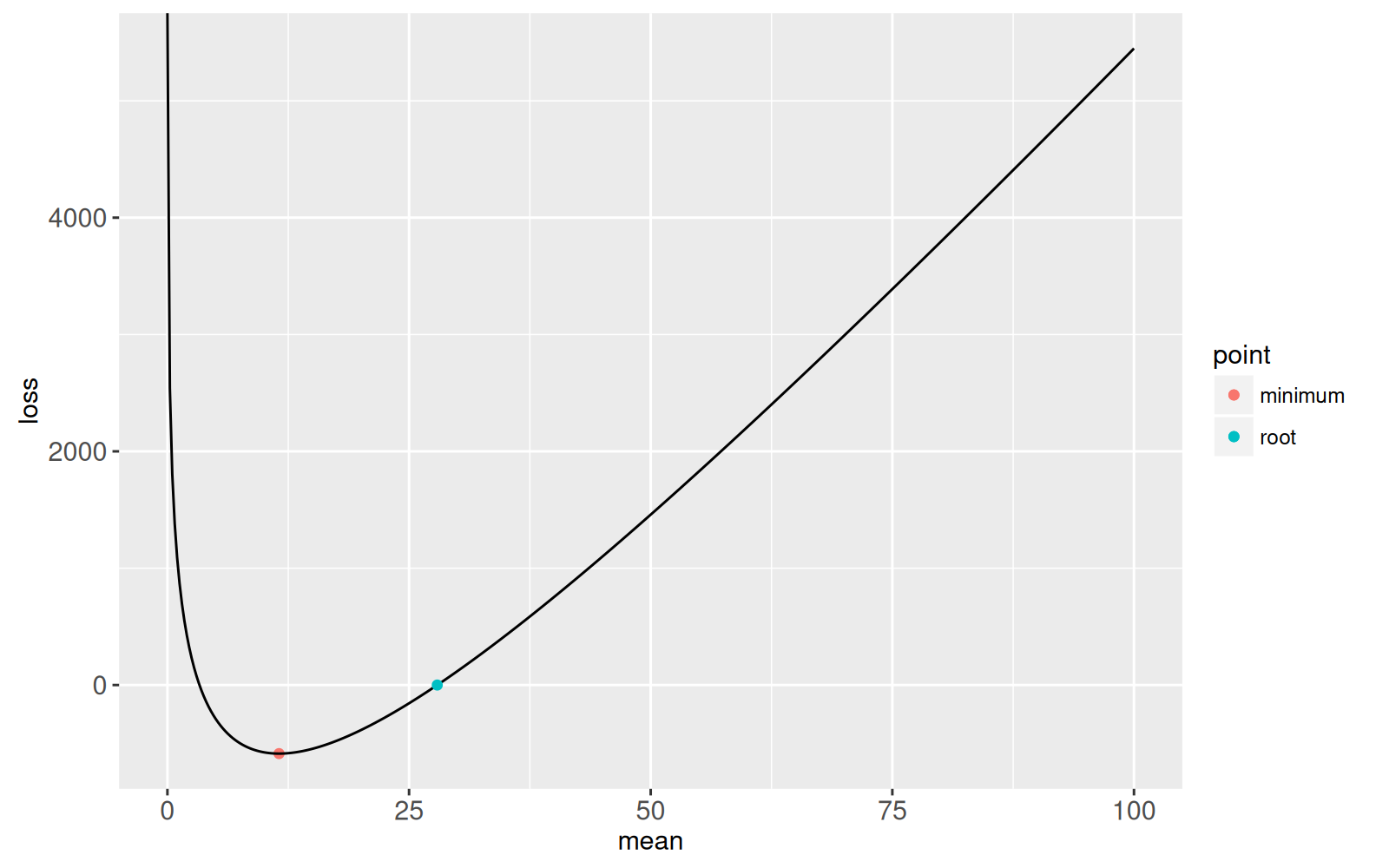
Le graphique ci-dessus montre la racine qui a été trouvée.
<!-- comment -->
Le critère d'arrêt était une valeur de coût absolu inférieure à `1e-6`, nous savons donc que cette racine est au moins aussi précise que ça.
<!-- comment -->
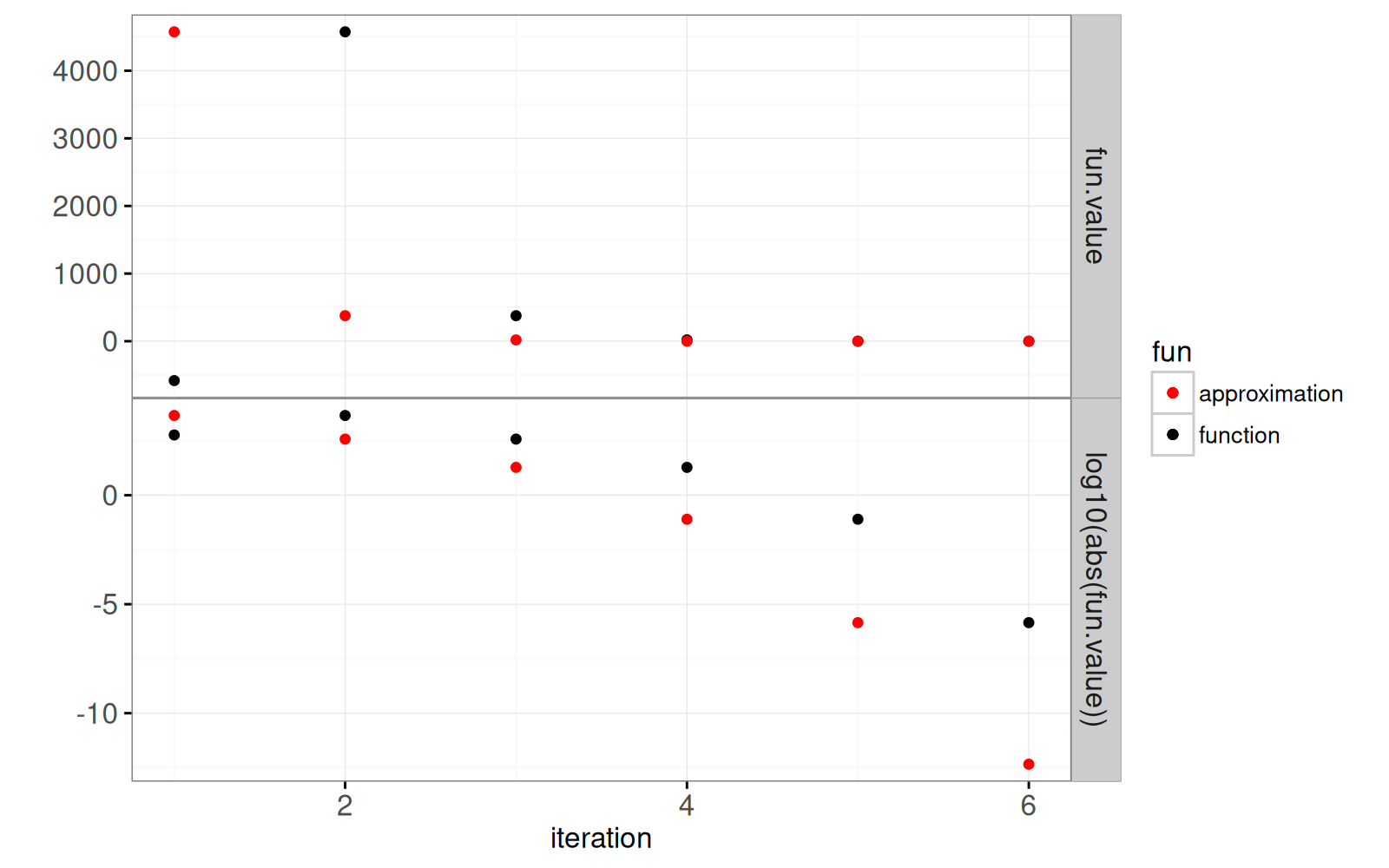
Le graphique suivant montre la précision de la racine en fonction du nombre d'itérations.
<!-- paragraph -->
```{r}
solution <- do.call(rbind, solution.list)
solution$new.value <- c(solution$fun.value[-1], fun.value)
gg.it <- ggplot()+
geom_point(aes(
iteration, fun.value, color=fun),
data=data.table(solution, y="fun.value", fun="function"))+
geom_point(aes(
iteration, log10(abs(fun.value)), color=fun),
data=data.table(
solution, y="log10(abs(fun.value))", fun="function"))+
scale_color_manual(values=c("function"="black", approximation="red"))+
geom_point(aes(
iteration, new.value, color=fun),
data=data.table(solution, y="fun.value", fun="approximation"))+
geom_point(aes(
iteration, log10(abs(new.value)), color=fun),
data=data.table(
solution, y="log10(abs(fun.value))", fun="approximation"))+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
facet_grid(y ~ ., scales="free")+
ylab("")
print(gg.it)
```
<!-- paragraph -->
Le graphique ci-dessus montre une ligne horizontale pour le seuil du critère d'arrêt sur l'échelle logarithmique.
<!-- comment -->
Il est clair que le point rouge de la dernière itération se situe bien en dessous de ce seuil.
<!-- paragraph -->
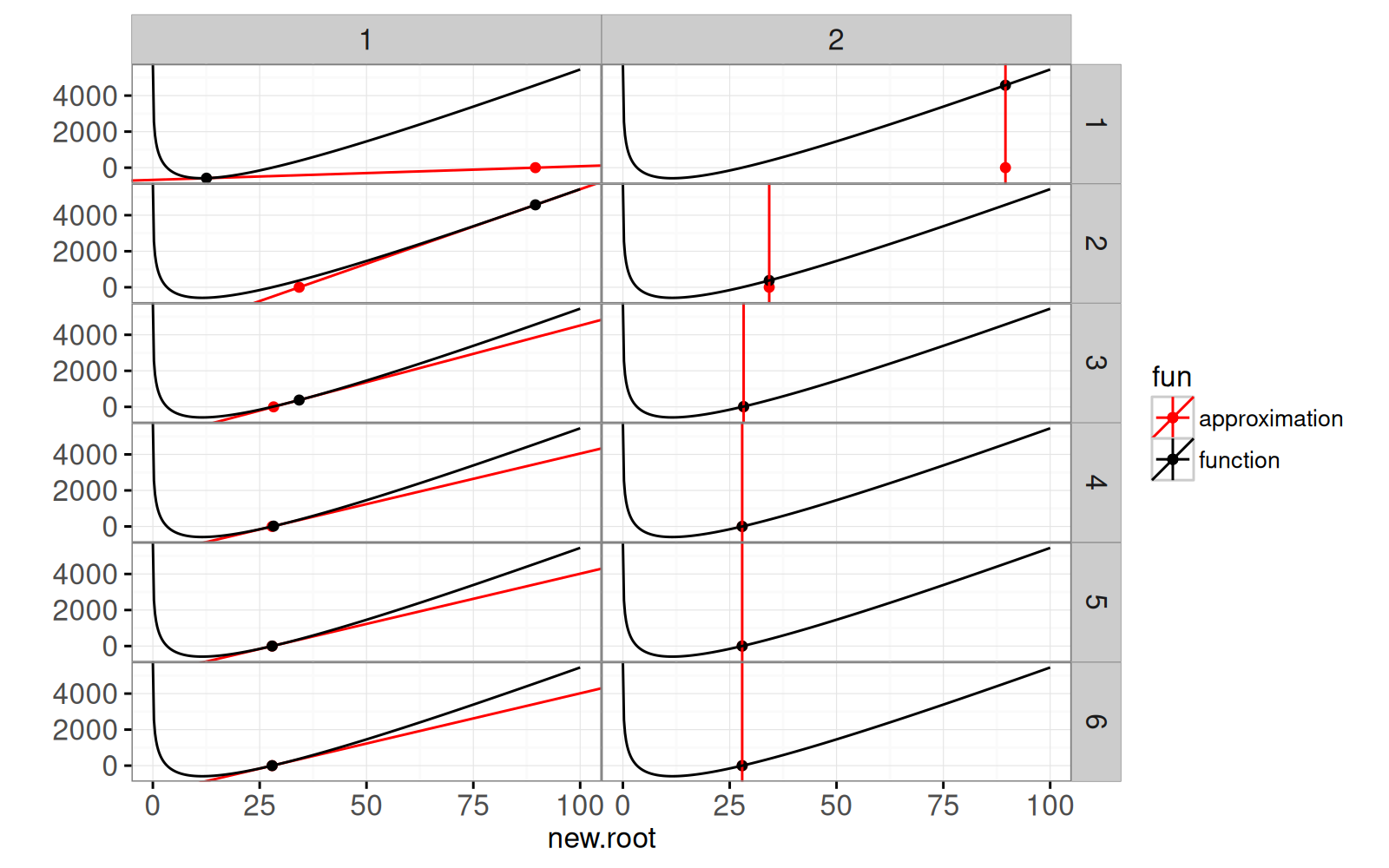
Le graphique ci-dessous montre chaque étape de l'algorithme.
<!-- comment -->
Les panneaux de gauche montrent l'approximation linéaire de la racine candidate, ainsi que la racine de l'approximation linéaire.
<!-- comment -->
Les panneaux de droite montrent la racine de l'approximation linéaire, ainsi que la valeur de la fonction correspondante (la nouvelle racine candidate).
<!-- paragraph -->
```{r}
## y - fun.value = deriv.value * (x - possible.root)
## y = deriv.value*x + fun.value-possible.root*deriv.value
ggplot()+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
facet_grid(iteration ~ step)+
scale_color_manual(values=c("function"="black", approximation="red"))+
geom_abline(aes(
slope=deriv.value, intercept=fun.value-possible.root*deriv.value,
color=fun),
data=data.table(solution, fun="approximation", step=1))+
geom_point(aes(
new.root, 0, color=fun),
data=data.table(solution, fun="approximation"))+
geom_point(aes(
new.root, new.value, color=fun),
data=data.table(solution, fun="function", step=2))+
geom_vline(aes(
xintercept=new.root, color=fun),
data=data.table(solution, fun="approximation", step=2))+
geom_point(aes(
possible.root, fun.value, color=fun),
data=data.table(solution, fun="function", step=1))+
geom_line(aes(
mean, loss, color=fun),
data=data.table(loss.dt, fun="function"))+
ylab("")
```
<!-- paragraph -->
Il est clair que l'algorithme converge rapidement vers la racine.
<!-- comment -->
Ce qui suit est une version interactive animée de la même visualisation des données.
<!-- paragraph -->
```{r Ch15-viz}
animint(
time=list(variable="iteration", ms=2000),
iterations=gg.it+
theme_animint(width=300, colspan=1)+
geom_tallrect(aes(
xmin=iteration-0.5,
xmax=iteration+0.5),
clickSelects="iteration",
alpha=0.5,
data=solution),
loss=ggplot()+
theme_bw()+
scale_color_manual(values=c(
"function"="black",
approximation="red"))+
geom_abline(aes(
slope=deriv.value, intercept=fun.value-possible.root*deriv.value,
color=fun),
showSelected="iteration",
data=data.table(solution, fun="approximation"))+
geom_point(aes(
new.root, 0, color=fun),
showSelected="iteration",
size=4,
data=data.table(solution, fun="approximation"))+
geom_point(aes(
new.root, new.value, color=fun),
showSelected="iteration",
data=data.table(solution, fun="function"))+
geom_vline(aes(
xintercept=new.root, color=fun),
showSelected="iteration",
data=data.table(solution, fun="approximation"))+
geom_point(aes(
possible.root, fun.value, color=fun),
showSelected="iteration",
data=data.table(solution, fun="function"))+
geom_line(aes(
mean, loss, color=fun),
data=data.table(loss.dt, fun="function"))+
ylab(""))
```
<!-- paragraph -->
## Comparaison avec la solution W de Lambert {#lambert}
<!-- paragraph -->
Le code ci-dessous utilise la fonction W de Lambert pour calculer une racine et compare la solution trouvée à celle calculée par la méthode de Newton.
<!-- paragraph -->
```{r compare-lambert}
inside <- Linear*exp(-Constant/Log)/Log
root.vec <- Log/Linear*c(
LambertW::W(inside, 0),
LambertW::W(inside, -1))
loss.fun(c(
Newton=root.dt$possible.root,
Lambert=root.vec[2]))
```
<!-- paragraph -->
Pour ces données, on obtient grâce à la fonction W de Lambert une racine légèrement plus précise qu'avec l'implémentation de la méthode de Newton.
<!-- paragraph -->
## Recherche de racine dans l'espace logarithmique {#log-space}
<!-- paragraph -->
Dans la section précédente nous avons présenté un algorithme pour trouver la racine qui est plus grande que le minimum.
<!-- comment -->
Dans cette section, nous explorons un algorithme permettant de trouver l'autre racine (plus petite que le minimum).
<!-- comment -->
Notez que la perte de Poisson est fortement non linéaire lorsque la moyenne s'approche de zéro, de sorte que l'approximation linéaire dans la recherche de racine de Newton ne fonctionnera pas très bien.
<!-- comment -->
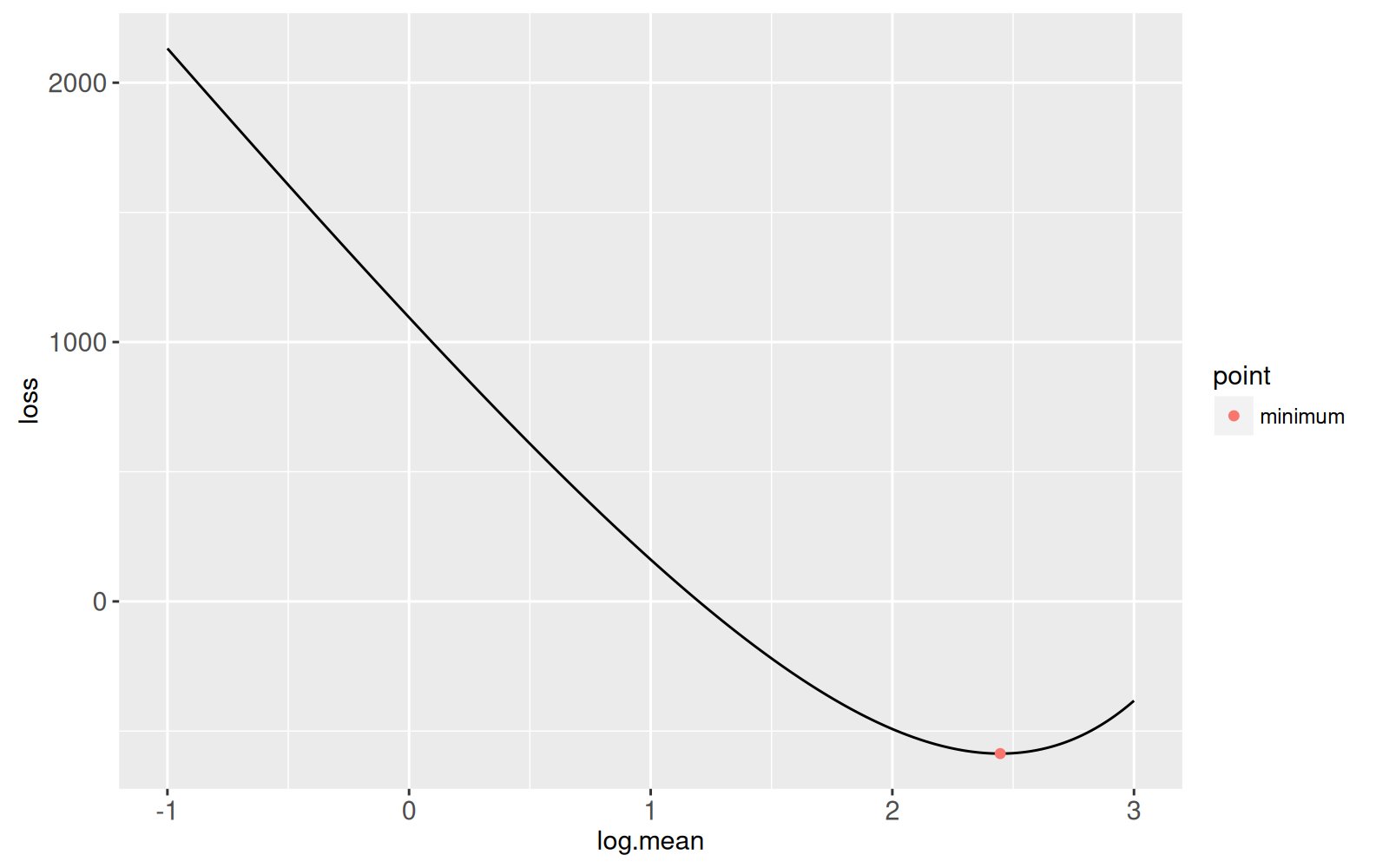
Pour contourner ce problème, nous effectuons une recherche de racine équivalente dans l'espace logarithmique :
<!-- paragraph -->
```{r logloss}
log.loss.fun <- function(log.mean){
Linear*exp(log.mean) + Log*log.mean + Constant
}
log.loss.dt <- data.table(
log.mean=seq(-1, 3, l=400)
)[
, loss := log.loss.fun(log.mean)]
ggplot()+
geom_line(aes(
log.mean, loss),
data=log.loss.dt)+
geom_point(aes(
log(mean), loss, color=point),
data=opt.dt)
```
<!-- paragraph -->
**Exercice :**
Dérivez et implémentez la méthode de Newton pour cette fonction, afin de trouver la racine qui est plus petite que le minimum.
<!-- comment -->
Créez un `animint2` similaire à la section précédente.
<!-- paragraph -->
## Résumé du chapitre et exercices {#Ch15-exercises}
<!-- paragraph -->
Dans ce chapitre, nous avons exploré plusieurs visualisations de la méthode de Newton pour trouver les racines de fonctions en douceur.
<!-- paragraph -->
Exercices :
<!-- paragraph -->
- Ajoutez un titre à chaque graphique.
<!-- comment -->
- Ajoutez une légende de taille au premier graphique (des points noirs plus grands que les rouges), afin qu'on puisse voir les cas où les points ont la même valeur.
<!-- comment -->
- Ajoutez une `geom_hline` pour mettre en évidence la valeur de perte=0 dans le second graphique.
<!-- comment -->
- Ajoutez un `geom_hline` pour mettre en évidence le seuil d'arrêt dans le premier graphique.
<!-- comment -->
- Désactivez l'une des deux légendes pour gagner de la place.
<!-- comment -->
- Comment spécifier des transitions graduelles entre les itérations?
<!-- comment -->
- Au lieu d'utiliser l'itération comme variable d'animation/de temps, créez-en une nouvelle afin de montrer deux états/étapes distincts pour chaque itération, c.-à-d.
<!-- comment -->
la variable `step` dans le graphique à facettes ci-dessus.
<!-- comment -->
- Qu'arrive-t-il au taux de convergence lorsque vous essayez de trouver la racine la plus grande dans l'espace logarithmique, ou la racine la plus petite dans l'espace original ?
<!-- comment -->
Théoriquement, la convergence devrait être moins rapide, car les fonctions sont plus fortement non linéaires pour ces racines.
<!-- comment -->
Réalisez une visualisation des données vous permettant de sélectionner la valeur de départ et qui montre le nombre d'itérations nécessaires pour converger, en respectant le seuil.
<!-- comment -->
- Créez un autre graphique permettant de sélectionner le seuil.
<!-- comment -->
Tracez le nombre d'itérations en fonction du seuil.
<!-- comment -->
- Dérivez la fonction de perte pour la [régression binomiale](https://en.wikipedia.org/wiki/Binomial_regression) et visualisez la méthode de recherche de racines de Newton correspondante.
<!-- comment -->
- Refactorisez `gg.it` pour n'utiliser qu'un seul `geom_point` au lieu des quatre geoms du code actuel.
<!-- comment -->
Conseil : utilisez `rbind()` pour créer un seul tableau avec toutes les données.
<!-- paragraph -->
Ensuite, dans le [chapitre 16](../Ch16/Ch16-change-point.html), nous vous expliquerons comment visualiser les modèles de détection des points de changement.
<!-- paragraph -->