# Séparateurs à vaste marge
<!-- paragraph -->
```{r setup, echo=FALSE}
knitr::opts_chunk$set(fig.path="Ch12-figures/")
```
<!-- paragraph -->
L'objectif de ce chapitre est de créer une visualisation des données interactive pour expliquer le concept de [séparateur à vaste marge](https://en.wikipedia.org/wiki/Support_vector_machine), un modèle d'apprentissage automatique pour la classification binaire.
<!-- paragraph -->
Résumé du chapitre :
<!-- paragraph -->
- Nous commençons par simuler des données pour une classification binaire en deux dimensions et nous les représentons par quelques graphiques statiques.
<!-- comment -->
- Dans la deuxième section, nous réalisons une visualisation des données interactive pour montrer comment la limite de décision du séparateur à vaste marge (SVM) linéaire varie en fonction de l'hyperparamètre de coût.
<!-- comment -->
- Dans la dernière section, nous réalisons une visualisation des données interactive pour montrer comment la limite de décision du séparateur à vaste marge à noyau polynomial varie en fonction des deux hyperparamètres (coût et degré).
<!-- paragraph -->
## Générer des données et les tracer {#generate}
<!-- paragraph -->
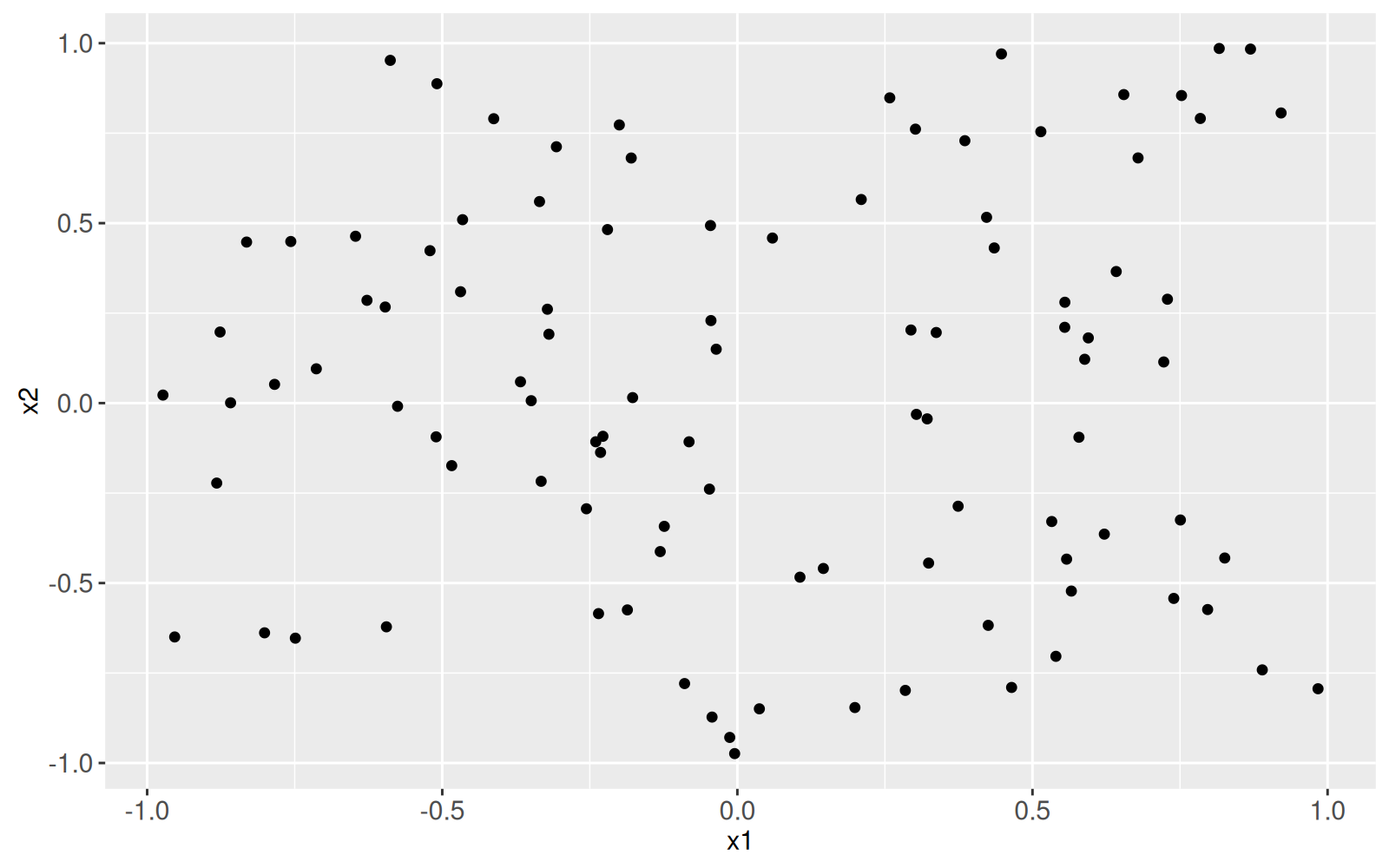
Nous commençons par générer deux fonctionnalités d'entrée, `x1` et `x2`.
<!-- paragraph -->
```{r}
library(data.table)
N <- 50
set.seed(1)
getInput <- function(){
c(#rnorm(N, sd=0.3),
runif(N, -1, 1),
runif(N, -1, 1)
)
}
data.dt <- data.table(
x1=getInput(),
x2=getInput())
library(animint2)
ggplot()+
geom_point(aes(
x1, x2),
data=data.dt)
```
<!-- paragraph -->
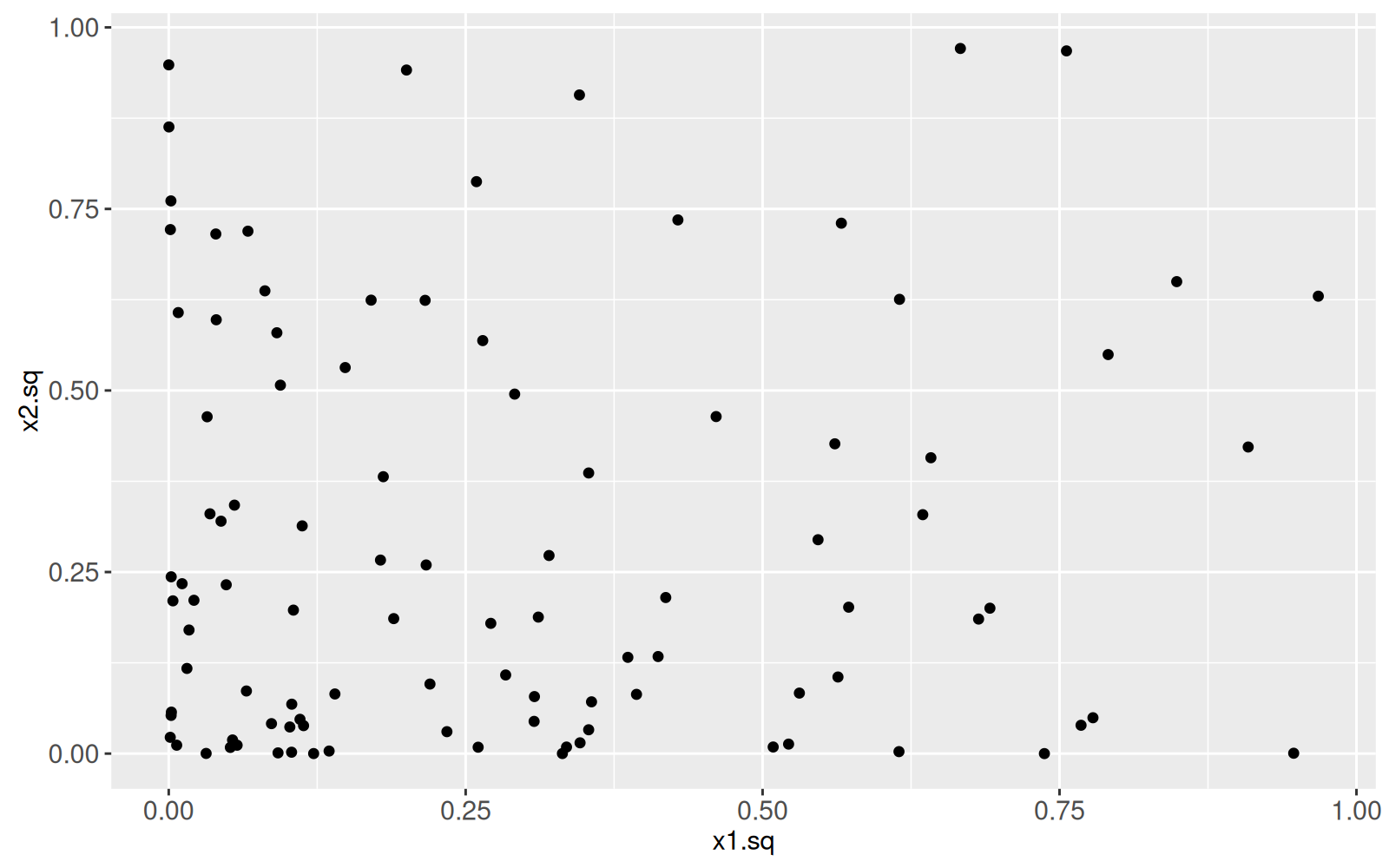
Le graphique ci-dessous montre les mêmes données, pour lesquelles deux fonctionnalités d'entrée supplémentaires ont été calculées (les carrés des deux entrées d'origine).
<!-- paragraph -->
```{r}
data.dt[, let(
x1.sq = x1^2,
x2.sq = x2^2)][]
ggplot()+
geom_point(aes(
x1.sq, x2.sq),
data=data.dt)
```
<!-- paragraph -->
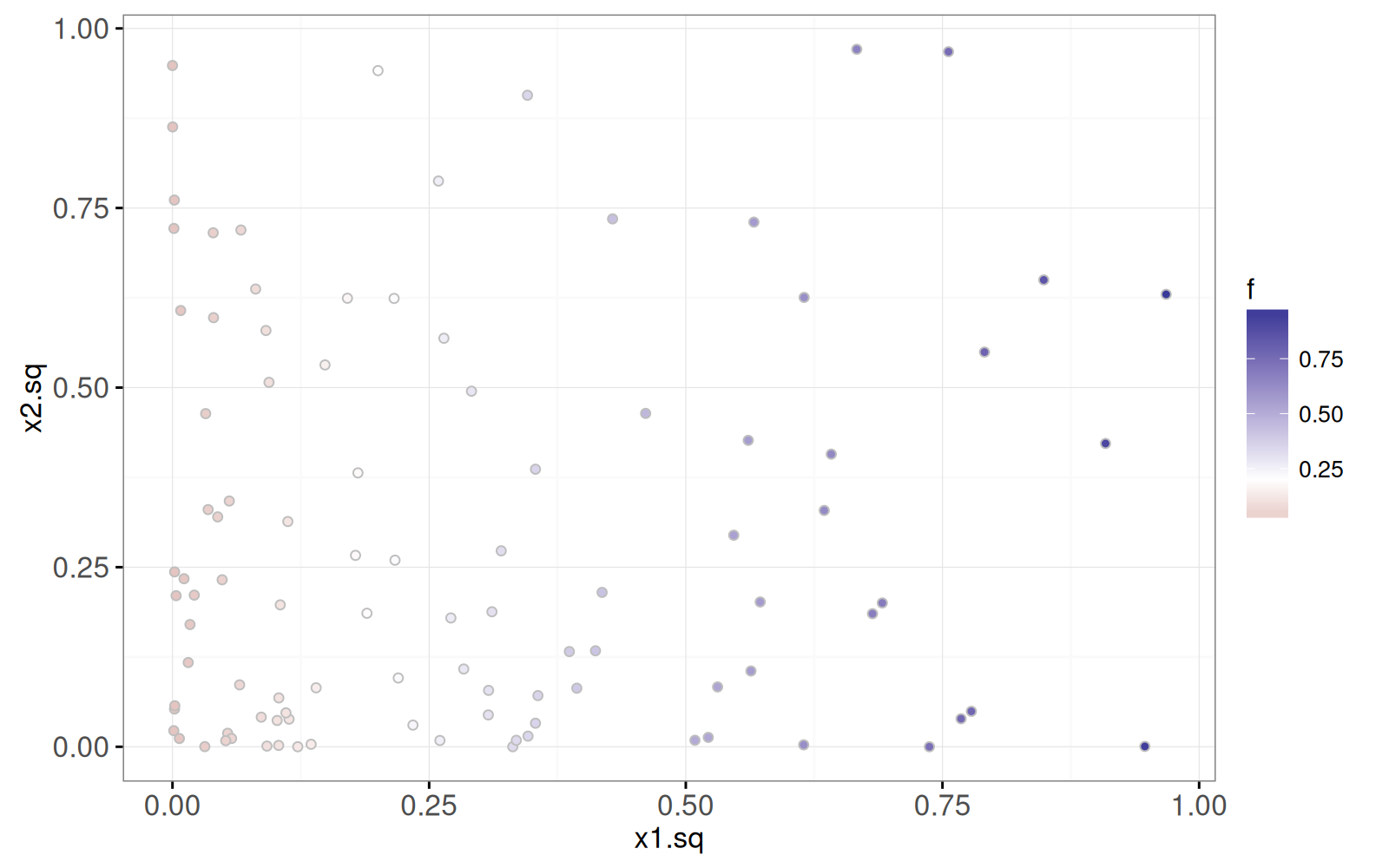
Dans notre simulation, nous supposons que le score de sortie `f` est une fonction linéaire de `x1.sq` et ne tient pas compte de `x2.sq`.
<!-- comment -->
Le graphique ci-dessous permet de visualiser les scores de sortie à l'aide de l'`aes()` de remplissage des points ("fill").
<!-- paragraph -->
```{r}
data.dt[, f := x1.sq]
true.decision.boundary <- 0.2
ggplot()+
theme_bw()+
scale_fill_gradient2(midpoint=true.decision.boundary)+
geom_point(aes(
x1.sq, x2.sq, fill=f),
shape=21,
color="grey",
data=data.dt)
```
<!-- paragraph -->
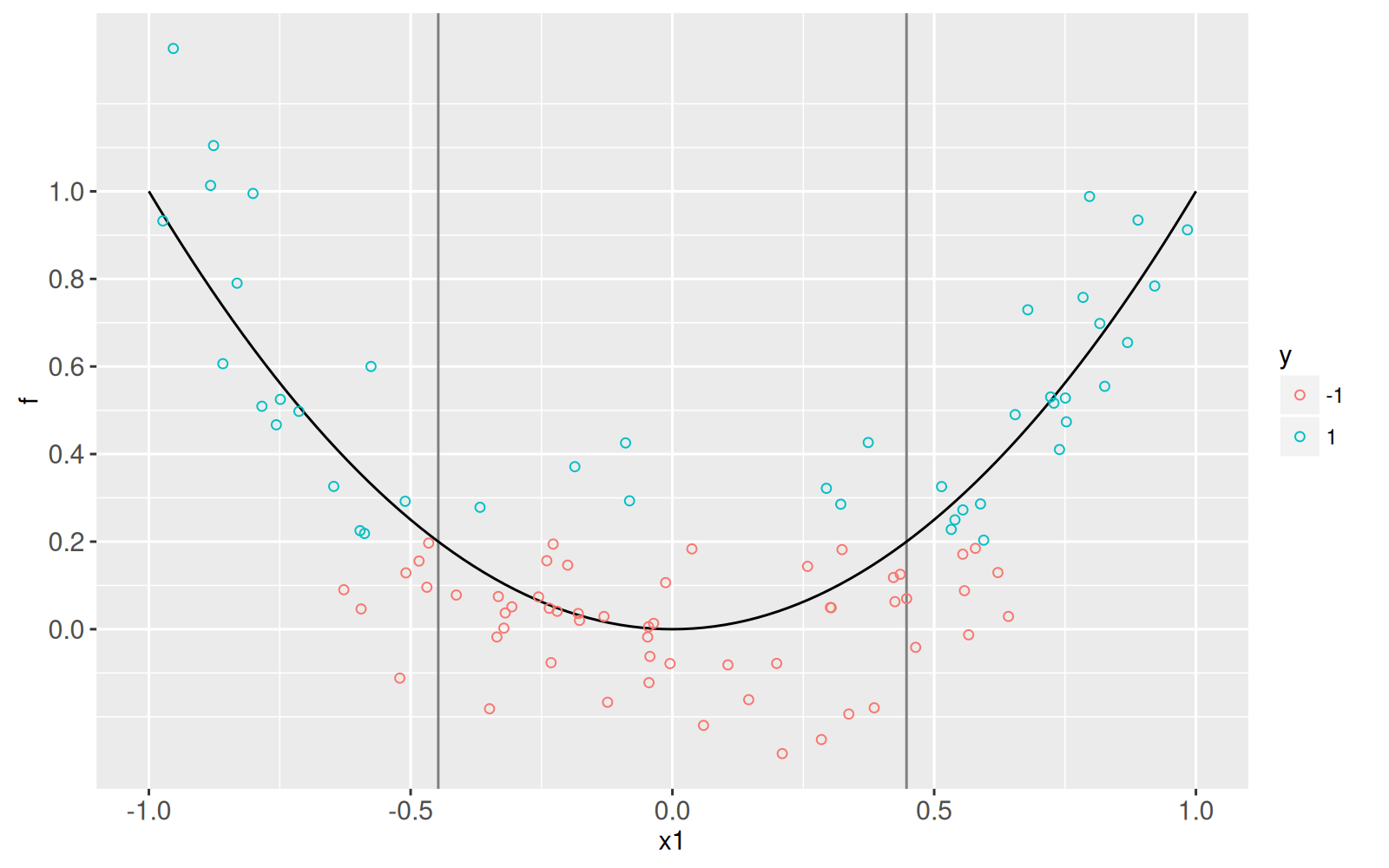
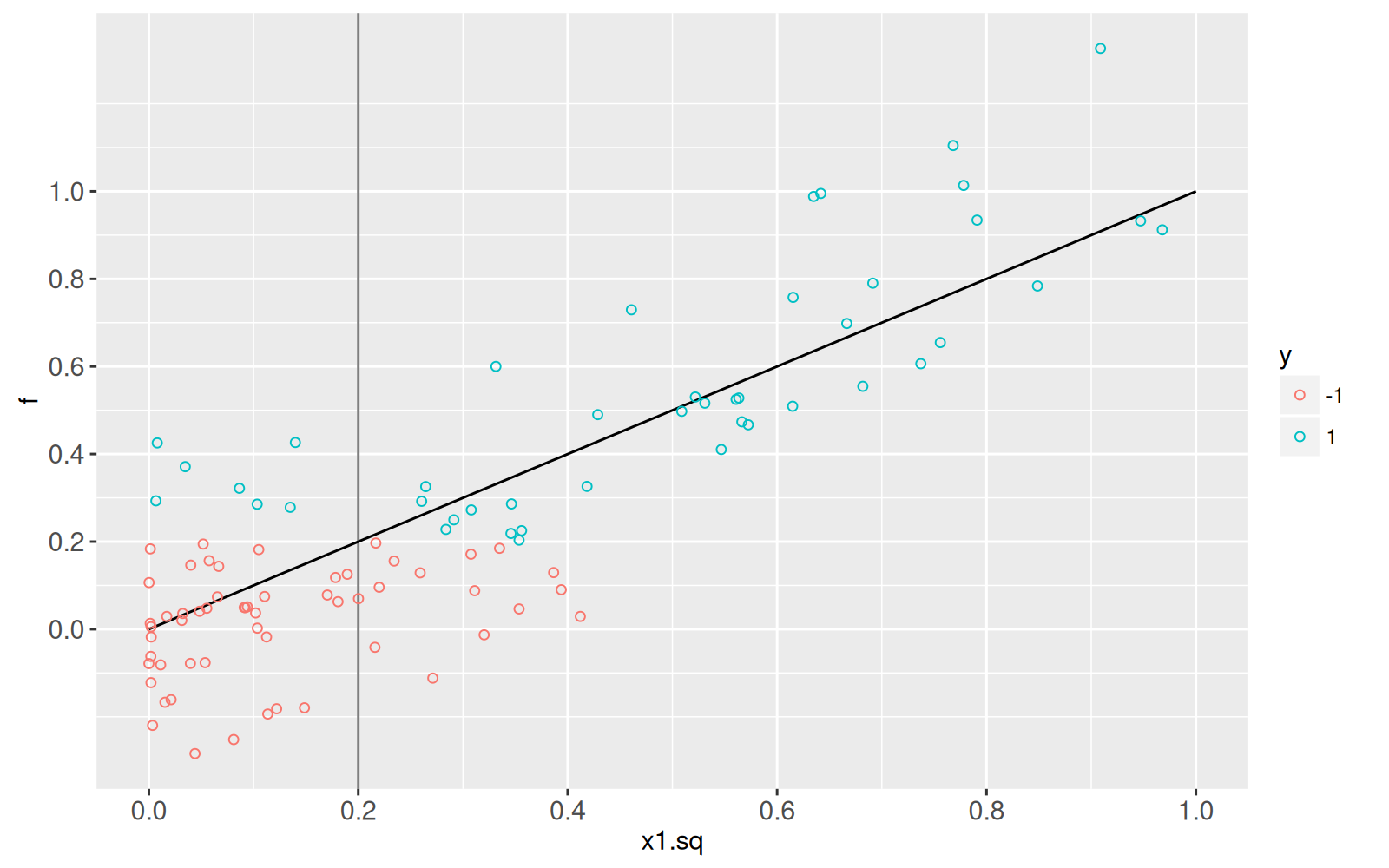
Concrètement, nous supposons que l'étiquette `y` est négative (-1) si `x1.sq + noise < threshold` et qu'elle est positive (1) dans le cas contraire.
<!-- comment -->
Le graphique ci-dessous permet de visualiser les scores et les étiquettes, en fonction de la fonctionnalité d'entrée `x1`.
<!-- comment -->
Le graphique montre aussi la fonction de score réel (en noir).
<!-- comment -->
Bien sûr, cette visualisation serait impossible avec des données réelles (seules les étiquettes sont connues dans les données réelles, pas les scores).
<!-- paragraph -->
```{r}
data.dt[
, f.noise := f+rnorm(N, 0, 0.2)
][
, y.num := ifelse(f.noise<true.decision.boundary, -1, 1)
][
, y := factor(y.num)
]
table(data.dt$y)
scores <- data.table(x1=seq(-1, 1, l=101))[
, x1.sq := x1^2
][
, f := x1.sq ]
x1.boundaries <- data.table(
boundary=c(1, -1)*sqrt(true.decision.boundary))
ggplot()+
scale_y_continuous(breaks=seq(0, 1, by=0.2))+
geom_vline(aes(
xintercept=boundary),
color="grey50",
data=x1.boundaries)+
geom_line(aes(
x1, f),
data=scores)+
geom_point(aes(
x1, f.noise, color=y),
shape=21,
fill=NA,
data=data.dt)
```
<!-- paragraph -->
Le graphique ci-dessous montre les scores et les étiquettes en fonction du carré de la fonctionnalité `x1.sq`.
<!-- comment -->
Il est clair que la fonction de score est linéaire par rapport à `x1.sq`.
<!-- paragraph -->
```{r}
x1sq.boundary <- data.table(boundary=true.decision.boundary)
ggplot()+
scale_y_continuous(breaks=seq(0, 1, by=0.2))+
scale_x_continuous(breaks=seq(0, 1, by=0.2))+
geom_vline(aes(
xintercept=boundary),
color="grey50",
data=x1sq.boundary)+
geom_line(aes(x1.sq, f), data=scores)+
geom_point(aes(
x1.sq, f.noise, color=y),
shape=21,
fill=NA,
data=data.dt)
```
<!-- paragraph -->
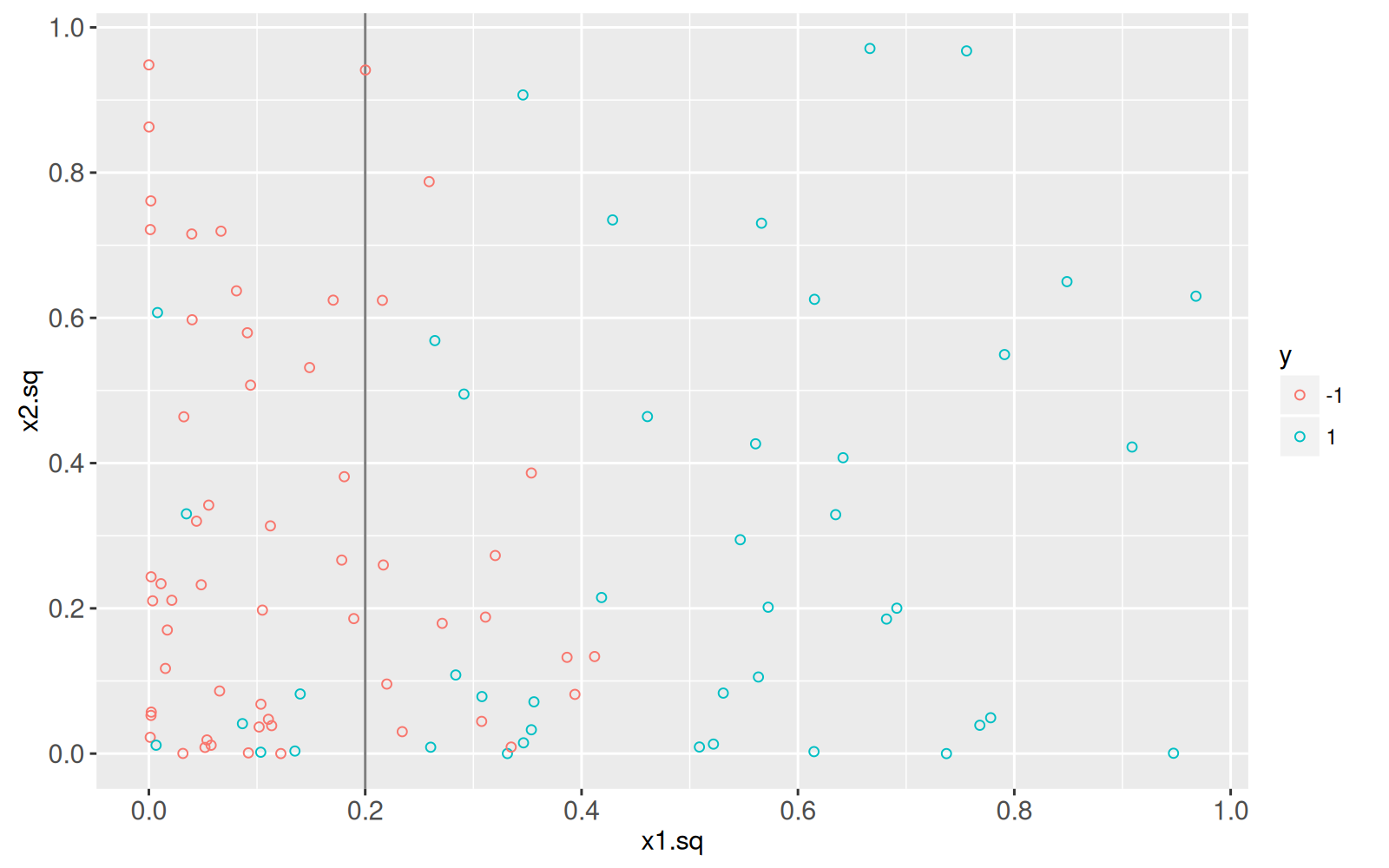
Ensuite, nous visualisons les étiquettes dans l'espace bidimensionnel des fonctionnalités au carré.
<!-- comment -->
Il est clair que la limite de décision est linéaire dans cet espace.
<!-- paragraph -->
```{r}
ggplot()+
scale_y_continuous(breaks=seq(0, 1, by=0.2))+
scale_x_continuous(breaks=seq(0, 1, by=0.2))+
geom_vline(aes(
xintercept=boundary),
color="grey50",
data=x1sq.boundary)+
geom_point(aes(
x1.sq, x2.sq, color=y),
shape=21,
fill=NA,
data=data.dt)
```
<!-- paragraph -->
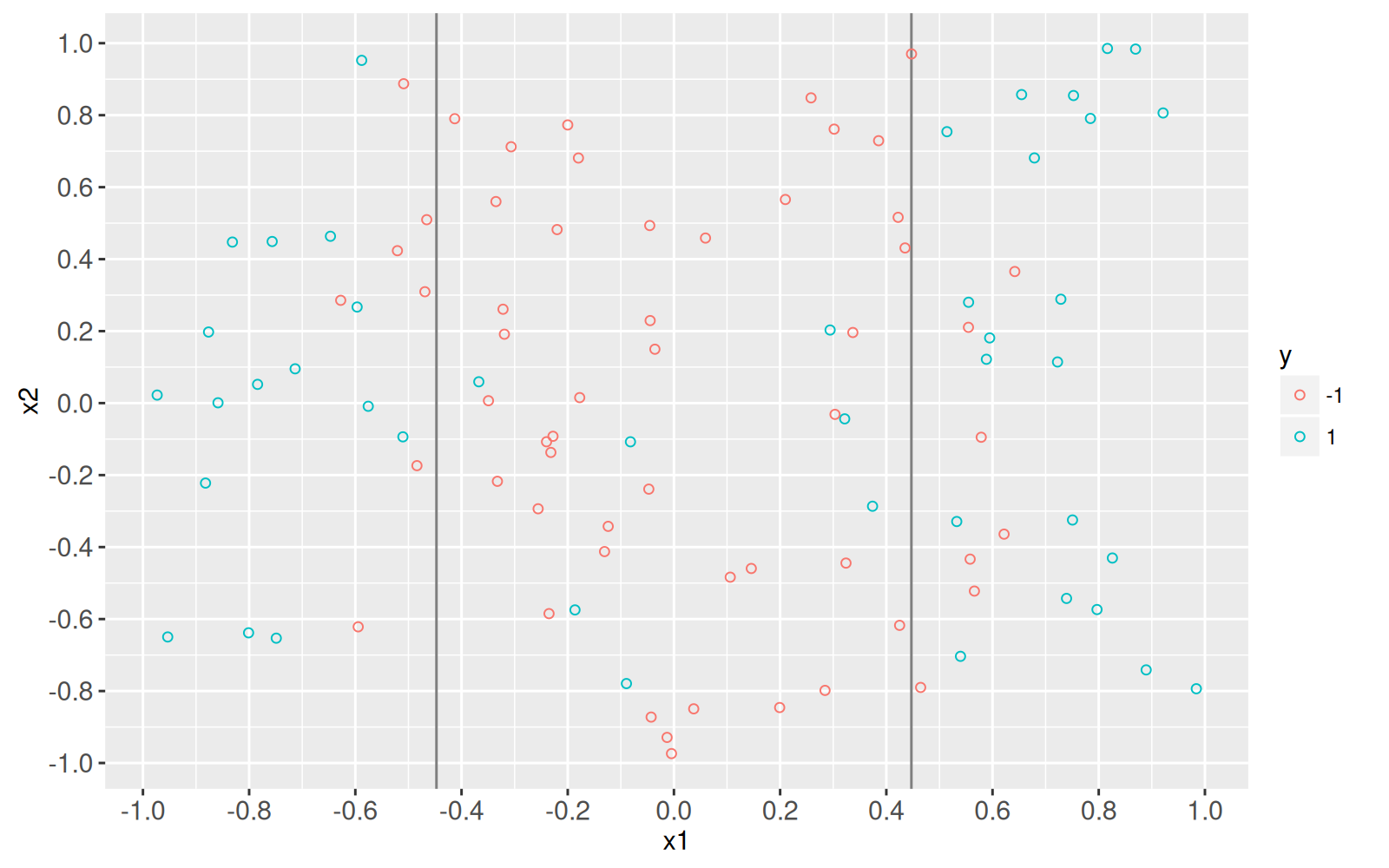
Le graphique ci-dessous montre l'espace des fonctionnalités d'entrée (`x1` et `x2`).
<!-- comment -->
Il est clair que la limite de décision n'est pas linéaire en `x1`.
<!-- paragraph -->
```{r}
ggplot()+
scale_y_continuous(breaks=seq(-1, 1, by=0.2))+
scale_x_continuous(breaks=seq(-1, 1, by=0.2))+
geom_vline(aes(
xintercept=boundary),
color="grey50",
data=x1.boundaries)+
geom_point(aes(
x1, x2, color=y),
shape=21,
fill=NA,
data=data.dt)
```
<!-- paragraph -->
L'`animint2` ci-dessous utilise `clickSelects` pour montrer les correspondances entre les points de l'espace d'entrée et de l'espace des fonctions au carré.
<!-- comment -->
Il suffit de créer un `data.i` qui possède un identifiant unique pour chaque point de données.
<!-- paragraph -->
```{r}
data.dt[, data.i := 1:.N]
YVAR <- function(dt, y.var){
dt$y.var <- factor(y.var, c("x2", "x2.sq", "f"))
dt
}
animint(
input=ggplot()+
ggtitle("espace des fonctionnalités d'entrée")+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
facet_grid(y.var ~ ., scales="free")+
scale_x_continuous(breaks=seq(-1, 1, by=0.2))+
ylab("")+
guides(color="none")+
geom_vline(aes(
xintercept=boundary),
color="grey50",
data=x1.boundaries)+
geom_point(aes(
x1, x2, color=y),
clickSelects="data.i",
size=4,
alpha=0.7,
data=YVAR(data.dt, "x2"))+
geom_line(aes(
x1, f),
data=YVAR(scores, "f"))+
geom_point(aes(
x1, f.noise, color=y),
clickSelects="data.i",
size=4,
alpha=0.7,
data=YVAR(data.dt, "f")),
square=ggplot()+
ggtitle("espace des fonctionnalités au carré")+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
facet_grid(y.var ~ ., scales="free")+
ylab("")+
scale_x_continuous(breaks=seq(0, 1, by=0.2))+
geom_vline(aes(
xintercept=boundary),
color="grey50",
data=x1sq.boundary)+
geom_point(aes(
x1.sq, x2.sq, color=y),
clickSelects="data.i",
size=4,
alpha=0.7,
data=YVAR(data.dt, "x2.sq"))+
geom_line(aes(
x1.sq, f),
data=YVAR(scores, "f"))+
geom_point(aes(
x1.sq, f.noise, color=y),
clickSelects="data.i",
size=4,
alpha=0.7,
data=YVAR(data.dt, "f")))
```
<!-- paragraph -->
Notez que nous avons utilisé deux graphiques multi-panneaux avec l'option [addColumn then facet](../Ch99/Ch99-appendix.html#addColumn-then-facet) au lieu de créer quatre graphiques distincts.
<!-- comment -->
Cela met l'accent sur le fait que certains graphiques/facettes ont un axe `x1` ou `x1.sq` commun.
<!-- comment -->
Notez que nous avons également masqué la légende des couleurs dans le premier graphique, puisqu'une seule légende suffit.
<!-- paragraph -->
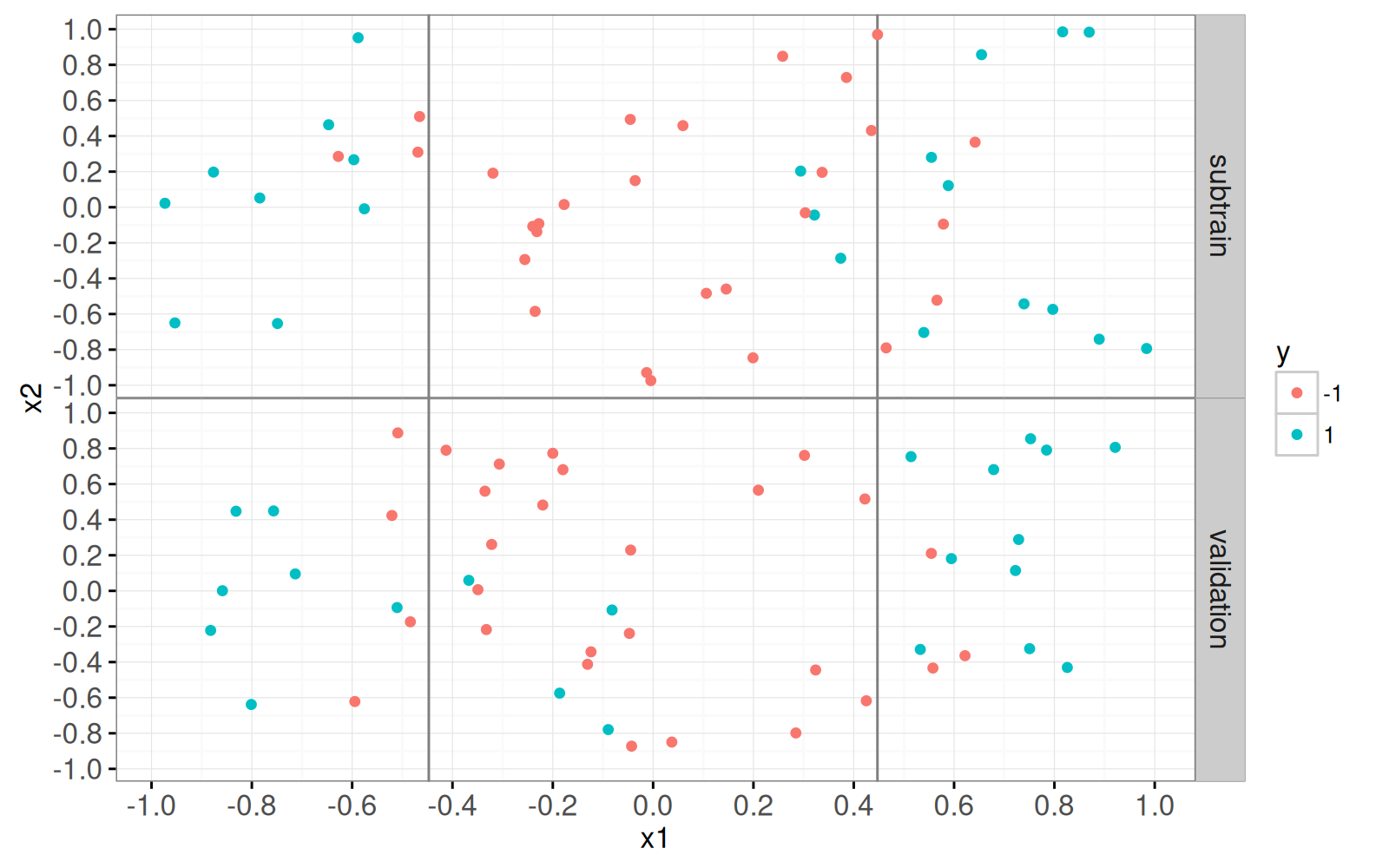
## SVM linéaire {#linear-svm}
<!-- paragraph -->
```{r}
train.i <- 1:N
data.dt[
, set := "validation"
][
train.i, set := "subtrain"
]
table(data.dt$set)
subtrain.dt <- data.dt[set=="subtrain",]
ggplot()+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
facet_grid(set ~ .)+
geom_vline(aes(
xintercept=boundary),
color="grey50",
data=x1.boundaries)+
scale_y_continuous(breaks=seq(-1, 1, by=0.2))+
scale_x_continuous(breaks=seq(-1, 1, by=0.2))+
geom_point(aes(
x1, x2, color=y),
data=data.dt)
```
<!-- paragraph -->
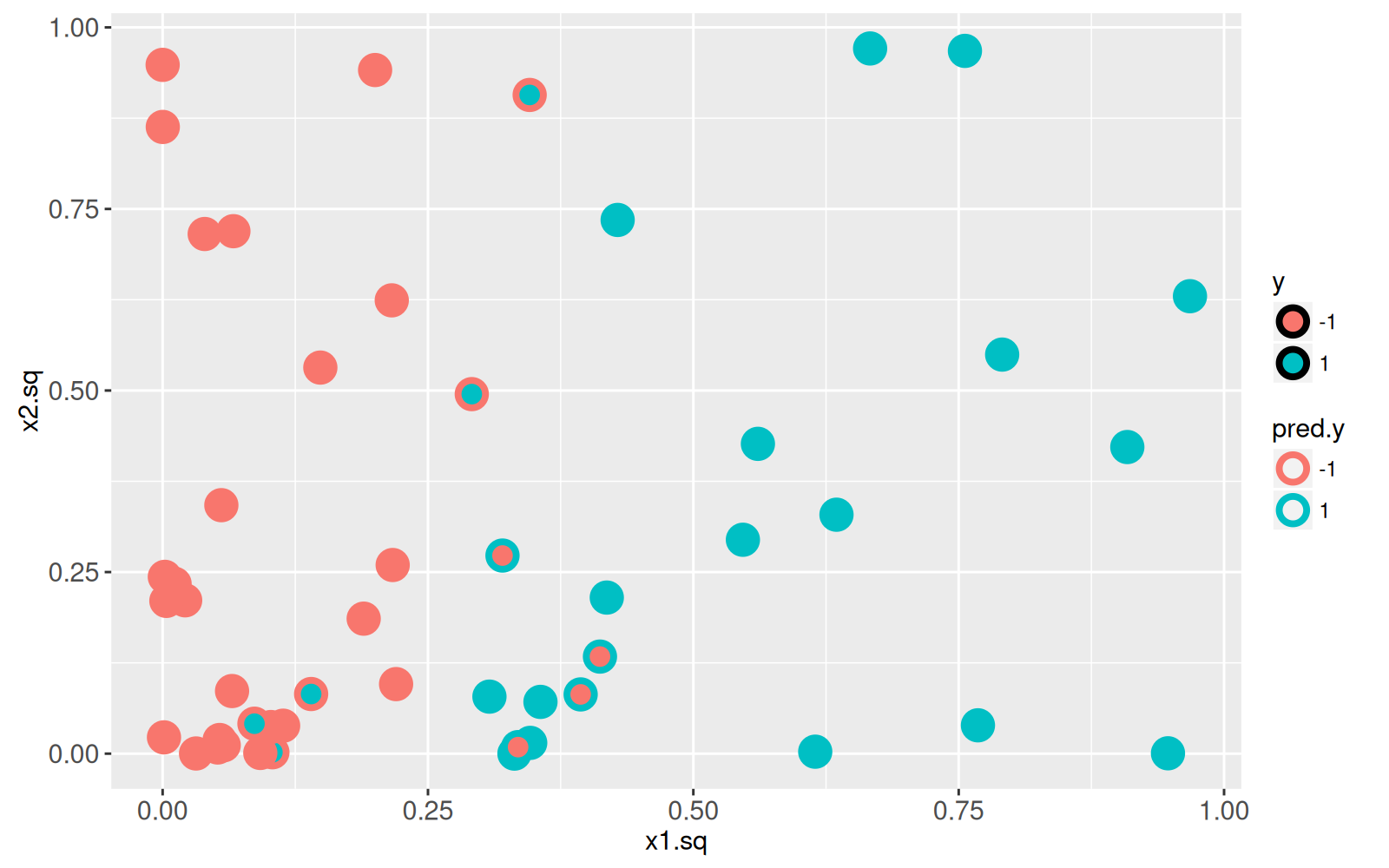
Nous commençons par ajuster un SVM linéaire aux données d'entraînement dans l'espace des fonctionnalités au carré, puis nous visualisons les vraies étiquettes `y` de même que les étiquettes prédites `pred.y`.
<!-- paragraph -->
```{r}
library(kernlab)
squared.mat <- subtrain.dt[, cbind(x1.sq, x2.sq)]
y.vec <- subtrain.dt$y
fit <- ksvm(squared.mat, y.vec, kernel="vanilladot")
subtrain.dt$pred.y <- predict(fit)
ggplot()+
geom_point(aes(
x1.sq, x2.sq, color=pred.y, fill=y),
shape=21,
size=4,
stroke=2,
data=subtrain.dt)
```
<!-- paragraph -->
Le graphique ci-dessus montre clairement qu'il existe plusieurs points de données d'entrainement mal classifiés.
<!-- comment -->
Le graphique ci-dessous permet de visualiser la limite de décision et la marge.
<!-- paragraph -->
```{r}
predF <- function(fit, X){
fit.sc <- scaling(fit)$x.scale
if(is.null(fit.sc)){
fit.sc <- list(
"scaled:center"=c(0,0),
"scaled:scale"=c(1,1))
}
mu <- fit.sc[["scaled:center"]]
sigma <- fit.sc[["scaled:scale"]]
X.sc <- scale(X, mu, sigma)
kernelMult(
kernelf(fit),
X.sc,
xmatrix(fit)[[1]],
coef(fit)[[1]])-b(fit)
}
xsq.vec <- seq(0, 1, l=41)
grid.sq.dt <- data.table(expand.grid(
x1.sq=xsq.vec,
x2.sq=xsq.vec
))[
, pred.f := predF(fit, cbind(x1.sq, x2.sq))]
subtrain.dt[, train.error := ifelse(y==pred.y, "correct", "error")]
ggplot()+
theme_bw()+
scale_color_manual(values=c(error="black", correct=NA))+
geom_point(aes(
x1.sq, x2.sq, fill=y, color=train.error),
shape=21,
stroke=1,
size=4,
data=subtrain.dt)+
geom_vline(aes(
xintercept=boundary), color="grey50",
data=x1sq.boundary)+
geom_contour(aes(
x1.sq, x2.sq, z=pred.f),
breaks=0,
color="black",
data=grid.sq.dt)+
geom_contour(aes(
x1.sq, x2.sq, z=pred.f),
breaks=c(-1, 1),
color="black",
linetype="dashed",
data=grid.sq.dt)
```
<!-- paragraph -->
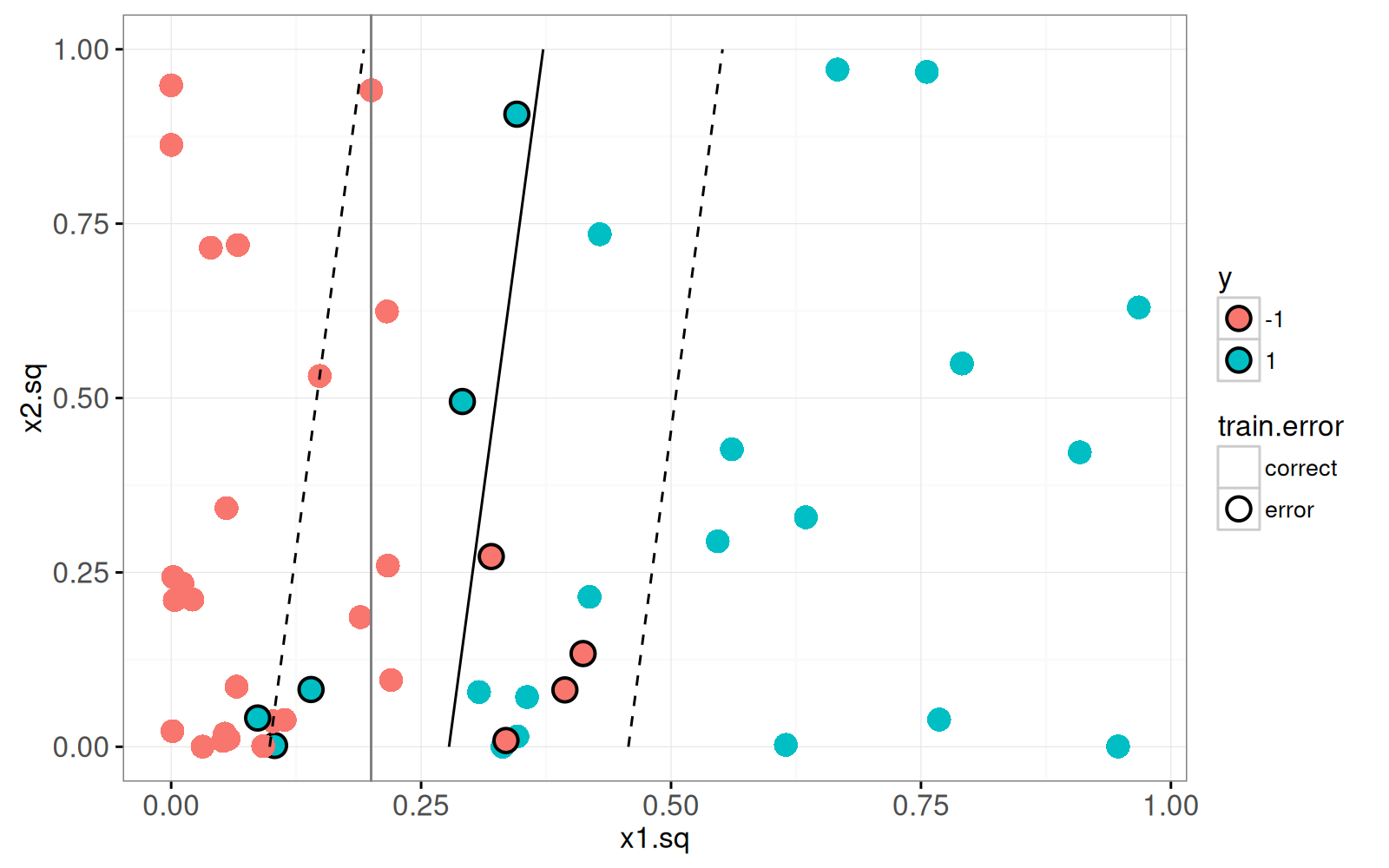
Le graphique ci-dessus montre la véritable limite de décision à l'aide d'un `vline` gris.
<!-- comment -->
Il utilise également`geom_contour` pour afficher la limite de décision (ligne noire continue, score prédit 0) et la marge (ligne noire pointillée, scores prédits -1 et 1).
<!-- comment -->
Puisque la limite de décision et la marge sont linéaires dans cet espace, nous pouvons également utiliser `geom_abline` pour les afficher.
<!-- comment -->
Pour ce faire, nous devons effectuer quelques calculs mathématiques et trouver les équations de la pente et de l'ordonnée à l'origine de ces droites (en fonction du biais appris `b(fit)` et du `weight.vec`, ainsi que des paramètres d'échelle `mu` et `sigma`).
<!-- paragraph -->
```{r}
## The equation of the margin lines is x2 = m2 + s2/w2[c+b+w1*m1/s1]
## -s2*w1/(w2*s1)*x1 for c=1 and -1. x is input feature, m is mean, s
## is scale, w is learned weight.
fit.sc <- scaling(fit)$x.scale
if(is.null(fit.sc)){
fit.sc <- list(
"scaled:center"=c(0,0),
"scaled:scale"=c(1,1))
}
mu <- fit.sc[["scaled:center"]]
sigma <- fit.sc[["scaled:scale"]]
weight.vec <- colSums(xmatrix(fit)[[1]]*coef(fit)[[1]])
predF.linear <- function(fit, X){
X.sc <- scale(X, mu, sigma)
X.sc %*% weight.vec - b(fit)
}
abline.dt <- data.table(
y=factor(c(-1,0,1)),
boundary=c("margin", "decision", "margin"),
intercept=mu[2]+sigma[2]/weight.vec[2]*(
c(-1, 0, 1)+b(fit)+weight.vec[1]*mu[1]/sigma[1]),
slope=-weight.vec[1]*sigma[2]/(weight.vec[2]*sigma[1]))
ggplot()+
theme_bw()+
scale_linetype_manual(values=c(margin="dashed", decision="solid"))+
geom_abline(aes(
slope=slope, intercept=intercept, linetype=boundary),
color="green",
size=1,
data=abline.dt)+
geom_point(aes(
x1.sq, x2.sq, color=y),
shape=21,
fill=NA,
size=4,
data=subtrain.dt)+
geom_contour(aes(
x1.sq, x2.sq, z=pred.f),
breaks=0,
color="black",
data=grid.sq.dt)+
geom_contour(aes(
x1.sq, x2.sq, z=pred.f),
breaks=c(-1, 1),
color="black",
linetype="dashed",
data=grid.sq.dt)
```
<!-- paragraph -->
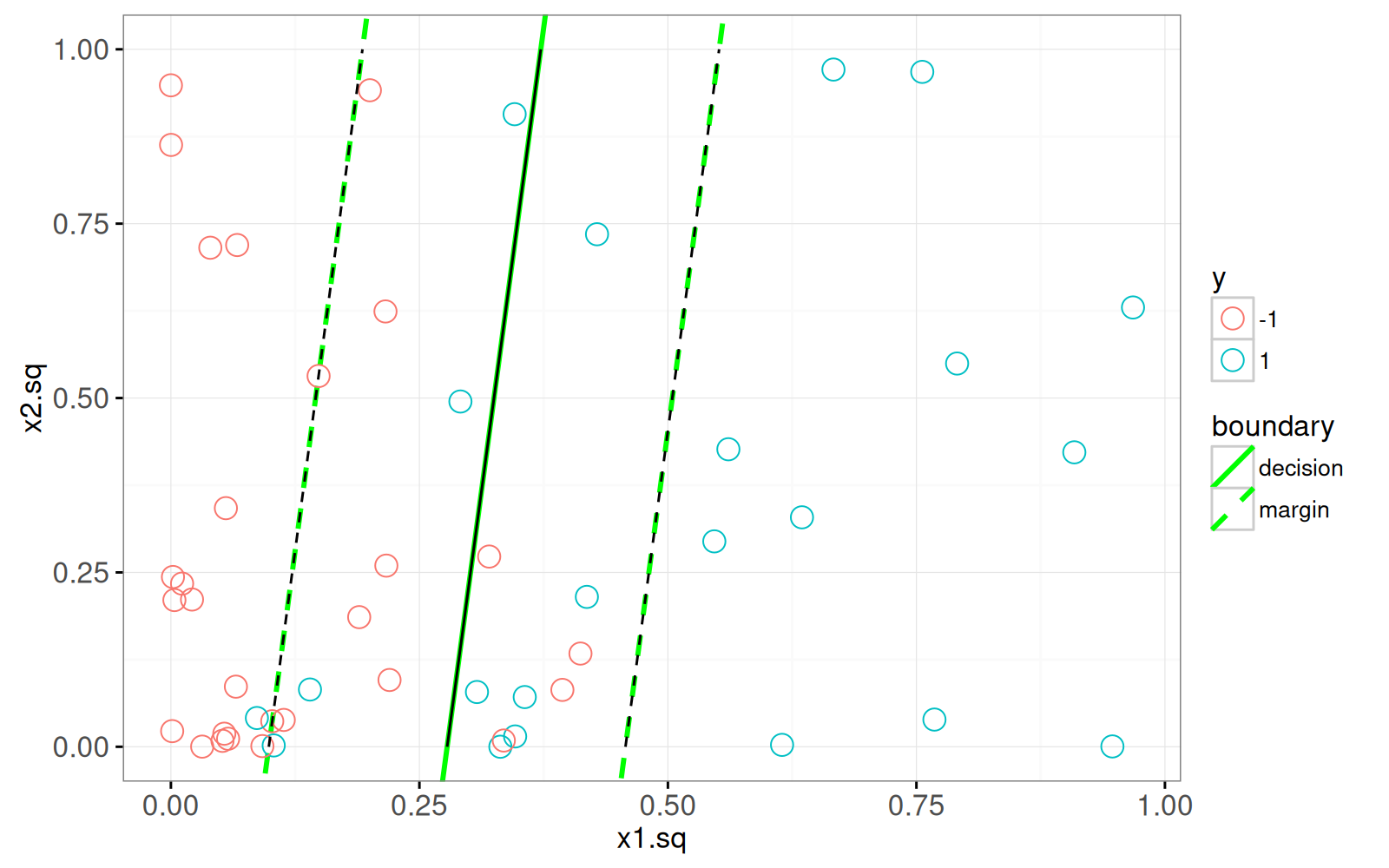
Le graphique ci-dessus confirme que notre calcul de la pente et des ordonnées à l'origine (lignes vertes) est en accord avec les contours (lignes noires).
<!-- comment -->
Dans le graphique ci-dessous, nous présentons les coefficients `alpha` appris et ajoutons un `geom_segment` pour visualiser la variable ressort (slack).
<!-- paragraph -->
```{r}
subtrain.dt[, alpha := 0]
train.row.vec <- as.integer(rownames(xmatrix(fit)[[1]]))
subtrain.dt[train.row.vec, alpha := kernlab::alpha(fit)[[1]] ]
subtrain.dt[, status := ifelse(
alpha==0, "alpha=0",
ifelse(alpha==1, "alpha=C", "0<alpha<C"))]
slack.slope <- weight.vec[2]*sigma[1]/(weight.vec[1]*sigma[2])
slack.dt <- subtrain.dt[alpha==1,]
slack.join <- abline.dt[slack.dt, on=list(y)]
slack.join[, x1.sq.margin := (
x2.sq-slack.slope*x1.sq-intercept)/(slope-slack.slope)]
slack.join[, x2.sq.margin := slope*x1.sq.margin + intercept]
sv.colors <- c(
"alpha=0"="white",
"0<alpha<C"="black",
"alpha=C"="grey")
ggplot()+
theme_bw()+
scale_linetype_manual(values=c(margin="dashed", decision="solid"))+
geom_vline(aes(
xintercept=boundary), color="violet",
data=x1sq.boundary)+
geom_abline(aes(
slope=slope, intercept=intercept, linetype=boundary),
size=1,
data=abline.dt)+
geom_segment(aes(
x1.sq, x2.sq,
xend=x1.sq.margin, yend=x2.sq.margin),
color="grey",
data=slack.join)+
scale_fill_manual(values=sv.colors, breaks=names(sv.colors))+
geom_point(aes(
x1.sq, x2.sq, color=y, fill=status),
shape=21,
size=4,
data=subtrain.dt)
```
<!-- paragraph -->
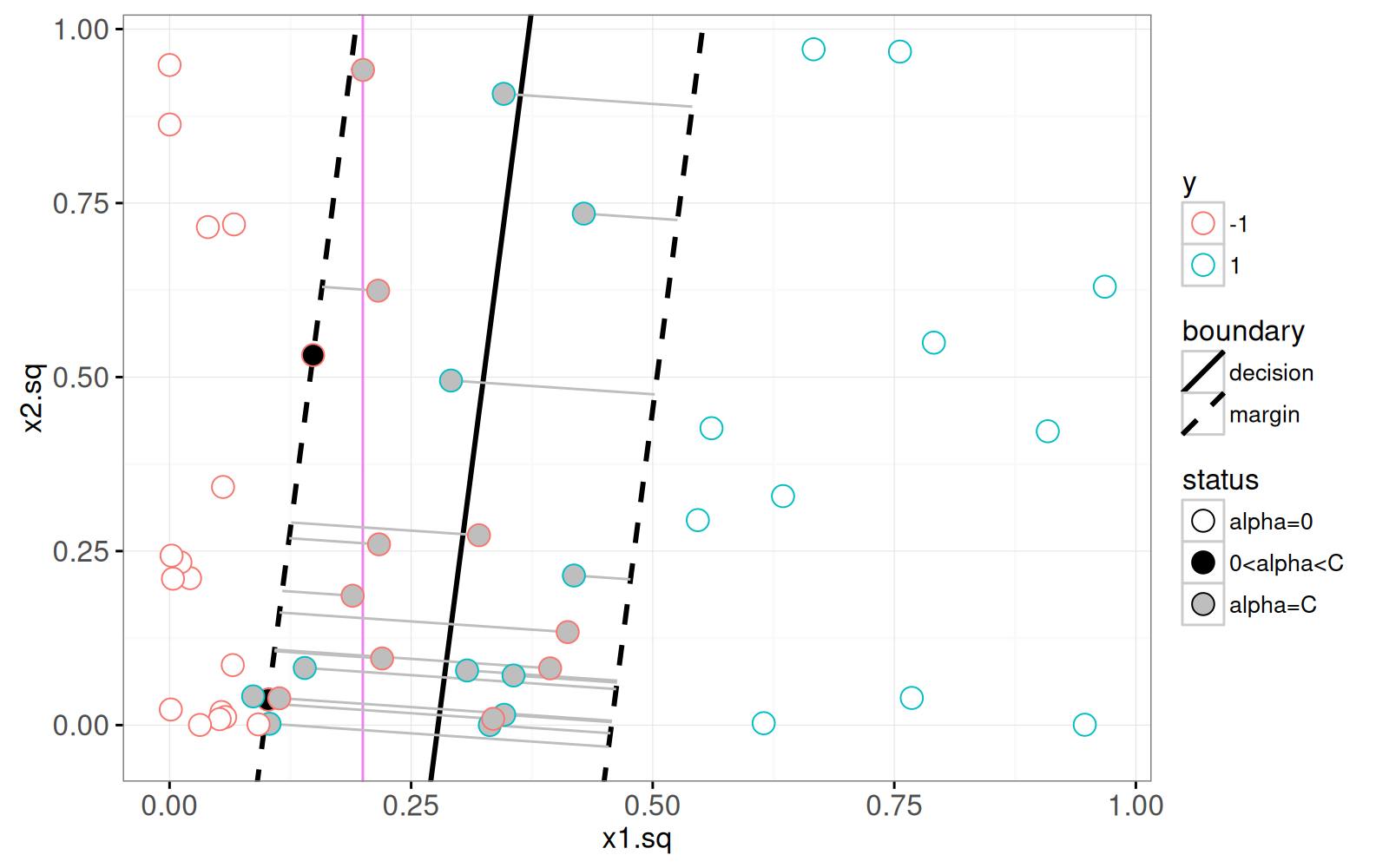
Le graphique ci-dessus montre le ressort (slack) dans les segments gris, et les lignes de décision et de marge en noir.
<!-- comment -->
La limite de décision de Bayes est représentée en arrière-plan par une ligne verticale violette.
<!-- comment -->
Les vecteurs de support sont les points pour lesquels les coefficients alpha ne sont pas nuls.
<!-- comment -->
Les vecteurs de support en noir (pleins) sont sur la marge et les vecteurs de support en gris sont du mauvais côté de la marge (et ont une marge de tolérance non nulle).
<!-- comment -->
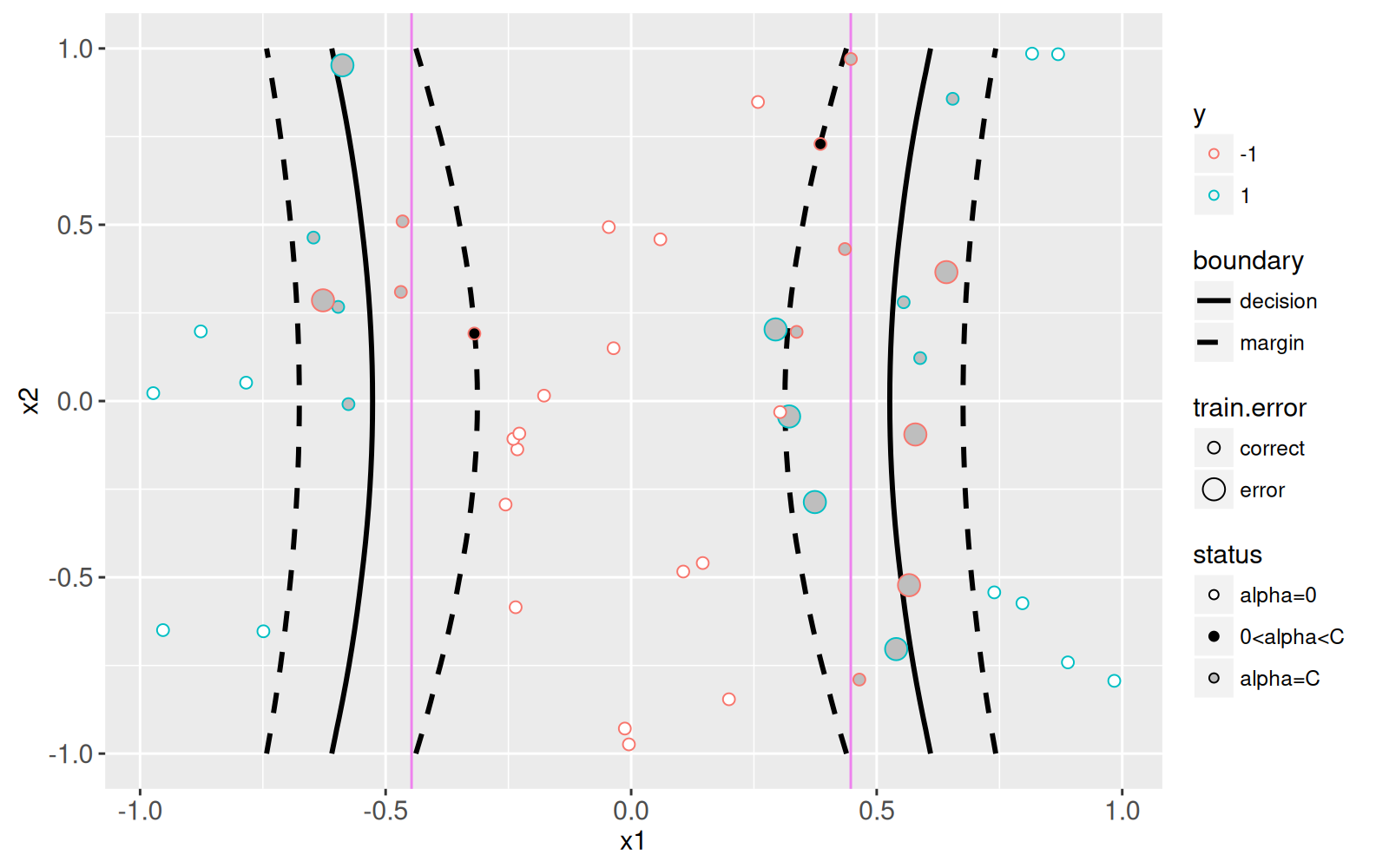
Le graphique ci-dessous montre le modèle qui a été appris dans l'espace des fonctionnalités d'origine.
<!-- paragraph -->
```{r}
n.grid <- 41
x.vec <- seq(-1, 1, l=n.grid)
grid.dt <- data.table(expand.grid(
x1=x.vec,
x2=x.vec))
getBoundaryDF <- function(score.vec, level.vec=c(-1, 0, 1)){
stopifnot(length(score.vec) == n.grid * n.grid)
several.paths <- contourLines(
x.vec, x.vec,
matrix(score.vec, n.grid, n.grid),
levels=level.vec)
contour.list <- list()
for(path.i in seq_along(several.paths)){
contour.list[[path.i]] <- with(several.paths[[path.i]], data.table(
path.i,
level.num=as.numeric(level),
level.fac=factor(level, level.vec),
boundary=ifelse(level==0, "decision", "margin"),
x1=x, x2=y))
}
do.call(rbind, contour.list)
}
grid.dt[, pred.f := predF(fit, cbind(x1^2, x2^2))]
boundaries <- grid.dt[, getBoundaryDF(pred.f)]
ggplot()+
scale_linetype_manual(values=c(margin="dashed", decision="solid"))+
geom_vline(aes(
xintercept=boundary),
color="violet",
data=x1.boundaries)+
geom_path(aes(
x1, x2, group=path.i, linetype=boundary),
size=1,
data=boundaries)+
scale_fill_manual(values=sv.colors, breaks=names(sv.colors))+
scale_size_manual(values=c(correct=2, error=4))+
geom_point(aes(
x1, x2, color=y,
size=train.error,
fill=status),
shape=21,
data=subtrain.dt)
```
<!-- paragraph -->
L'objectif de la démonstration ci-dessous est de créer un `animint2` qui montre comment la limite de décision, la marge et le ressort ("slack") évoluent en fonction du paramètre de coût.
<!-- paragraph -->
```{r Ch12-viz-linear}
modelInfo.list <- list()
predictions.list <- list()
slackSegs.list <- list()
modelLines.list <- list()
inputBoundaries.list <- list()
setErrors.list <- list()
cost.by <- 0.2
for(cost.param in round(10^seq(-1, 1, by=cost.by),1)){
fit <- ksvm(
squared.mat, y.vec, kernel="vanilladot", scaled=FALSE, C=cost.param)
fit.sc <- scaling(fit)$x.scale
if(is.null(fit.sc)){
fit.sc <- list(
"scaled:center"=c(0,0),
"scaled:scale"=c(1,1))
}
mu <- fit.sc[["scaled:center"]]
sigma <- fit.sc[["scaled:scale"]]
weight.vec <- colSums(xmatrix(fit)[[1]]*coef(fit)[[1]])
grid.sq.dt[, pred.f := predF(fit, cbind(x1.sq, x2.sq))]
data.dt[, pred.y := predict(fit, cbind(x1.sq, x2.sq))]
one.error <- data.dt[, list(errors=sum(y!=pred.y)), by=set]
setErrors.list[[paste(cost.param)]] <- data.table(
cost.param, one.error)
subtrain.dt[, pred.f := predF(fit, cbind(x1^2, x2^2))]
grid.dt[, pred.f := predF(fit, cbind(x1^2, x2^2))]
boundaries <- getBoundaryDF(grid.dt$pred.f)
inputBoundaries.list[[paste(cost.param)]] <- data.table(
cost.param, boundaries)
subtrain.dt$alpha <- 0
train.row.vec <- as.integer(rownames(xmatrix(fit)[[1]]))
subtrain.dt[train.row.vec, alpha := kernlab::alpha(fit)[[1]] ]
subtrain.dt[, status := ifelse(
alpha==0, "alpha=0",
ifelse(alpha==cost.param, "alpha=C", "0<alpha<C"))]
## The equation of the margin lines is x2 = m2 + s2/w2[c+b+w1*m1/s1]
## -s2*w1/(w2*s1)*x1 for c=1 and -1. x is input feature, m is mean, s
## is scale, w is learned weight.
slack.slope <- weight.vec[2]*sigma[1]/(weight.vec[1]*sigma[2])
abline.dt <- data.table(
y=factor(c(-1,0,1)),
boundary=c("margin", "decision", "margin"),
intercept=mu[2]+sigma[2]/weight.vec[2]*(
c(-1, 0, 1)+b(fit)+weight.vec[1]*mu[1]/sigma[1]),
slope=-weight.vec[1]*sigma[2]/(weight.vec[2]*sigma[1]))
slack.dt <- subtrain.dt[alpha==cost.param]
slack.join <- abline.dt[slack.dt, on=list(y)]
slack.join[, x1.sq.margin := (
x2.sq-slack.slope*x1.sq-intercept)/(slope-slack.slope)]
slack.join[, x2.sq.margin := slope*x1.sq.margin + intercept]
norm.weights <- as.numeric(weight.vec %*% weight.vec)
modelInfo.list[[paste(cost.param)]] <- data.table(
cost.param,
slack=slack.join[, sum(1-pred.f*y.num)],
norm=norm.weights,
margin=2/sqrt(norm.weights))
predictions.list[[paste(cost.param)]] <- data.table(
cost.param, subtrain.dt)
slackSegs.list[[paste(cost.param)]] <- data.table(
cost.param, slack.join)
modelLines.list[[paste(cost.param)]] <- data.table(
cost.param, abline.dt)
}
inputBoundaries <- do.call(rbind, inputBoundaries.list)
predictions <- do.call(rbind, predictions.list)
slackSegs <- do.call(rbind, slackSegs.list)
modelLines <- do.call(rbind, modelLines.list)
modelInfo <- do.call(rbind, modelInfo.list)
setErrors <- do.call(rbind, setErrors.list)
modelInfo.tall <- melt(modelInfo, id.vars="cost.param")
grid.sq.dt$boundary <- "true"
setErrors$variable <- "errors"
inputBoundaries[, boundary := ifelse(level.num==0, "decision", "margin")]
slackSegs$boundary <- "margin"
set.label.select <- data.table(
cost.param=range(setErrors$cost.param),
set=c("validation", "subtrain"),
hjust=c(1, 0))
set.labels <- setErrors[set.label.select, on=list(cost.param, set)]
viz.linear.svm <- animint(
selectModel=ggplot()+
ggtitle("Select regularization parameter")+
scale_x_continuous(limits=c(-1.5, 1.5))+
geom_tallrect(aes(
xmin=log10(cost.param)-cost.by/2,
xmax=log10(cost.param)+cost.by/2),
clickSelects="cost.param",
alpha=0.5,
data=modelInfo)+
theme_bw()+
facet_grid(variable ~ ., scales="free")+
geom_line(aes(
log10(cost.param), errors,
group=set, color=set),
data=setErrors)+
geom_text(aes(
log10(cost.param), errors-1, label=set,
hjust=hjust,
color=set),
data=set.labels)+
guides(color="none")+
geom_line(aes(
log10(cost.param), log10(value)),
data=modelInfo.tall),
inputSpace=ggplot()+
ggtitle("Input space features")+
scale_fill_manual(values=sv.colors, breaks=names(sv.colors))+
geom_vline(aes(
xintercept=boundary),
color="violet",
data=x1.boundaries)+
guides(color="none", fill="none", linetype="none")+
scale_linetype_manual(values=c(
"-1"="dashed",
"0"="solid",
"1"="dashed"))+
geom_path(aes(
x1, x2,
group=path.i,
linetype=level.fac),
showSelected=c("boundary", "cost.param"),
color="black",
data=inputBoundaries)+
geom_point(aes(
x1, x2, fill=status),
showSelected=c("status", "y", "data.i", "cost.param"),
size=5,
color="grey",
data=predictions)+
geom_point(aes(
x1, x2, color=y, fill=status),
showSelected=c("cost.param", "status", "y"),
clickSelects="data.i",
size=3,
data=predictions),
kernelSpace=ggplot()+
ggtitle("Kernel space features")+
geom_vline(aes(
xintercept=boundary), color="violet",
data=x1sq.boundary)+
##coord_cartesian(xlim=c(0, 1), ylim=c(0, 1))+
geom_abline(aes(
slope=slope, intercept=intercept, linetype=boundary),
showSelected="cost.param",
color="black",
data=modelLines)+
scale_linetype_manual(values=c(
decision="solid",
margin="dashed",
true="solid"))+
geom_point(aes(
x1.sq, x2.sq, fill=status),
showSelected=c("data.i", "cost.param"),
size=5,
color="grey",
data=predictions)+
geom_point(aes(
x1.sq, x2.sq, color=y, fill=status),
clickSelects="data.i",
showSelected="cost.param",
size=3,
data=predictions)+
scale_fill_manual(values=sv.colors, breaks=names(sv.colors))+
geom_segment(aes(
x1.sq, x2.sq,
xend=x1.sq.margin, yend=x2.sq.margin),
showSelected=c("cost.param", "boundary"),
color="grey",
data=slackSegs))
viz.linear.svm
```
<!-- paragraph -->
## SVM à noyau polynomial non linéaire {#nonlinear-polynomial-kernel-svm}
<!-- paragraph -->
Dans la section précédente, nous avons ajusté un noyau linéaire dans l'espace des fonctionnalités au carré, ce qui a entraîné l'apprentissage d'une fonction non linéaire en termes d'espace des fonctionnalités d'origine.
<!-- comment -->
Dans cette section, nous procédons à l'ajustement direct d'un noyau polynomial non linéaire dans l'espace d'origine.
<!-- paragraph -->
```{r Ch12-viz-poly}
predictions.list <- list()
inputBoundaries.list <- list()
setErrors.list <- list()
cost.by <- 0.2
orig.mat <- subtrain.dt[, cbind(x1, x2)]
for(cost.param in 10^seq(-1, 3, by=cost.by)){
for(degree.num in seq(1, 6, by=1)){
k <- polydot(degree.num, offset=0)
fit <- ksvm(
orig.mat, y.vec, kernel=k, scaled=FALSE, C=cost.param)
grid.dt[, pred.f := predF(fit, cbind(x1, x2))]
grid.dt[, pred.y := predict(fit, cbind(x1, x2))]
grid.dt[, stopifnot(sign(pred.f) == pred.y)]
data.dt[, pred.y := predict(fit, cbind(x1, x2))]
one.error <- data.dt[, list(errors=sum(y != pred.y)), by=set]
setErrors.list[[paste(cost.param, degree.num)]] <- data.table(
cost.param, degree.num, one.error)
boundaries <- getBoundaryDF(grid.dt$pred.f)
if(is.data.frame(boundaries) && nrow(boundaries)){
cost.deg <- paste(cost.param, degree.num)
inputBoundaries.list[[cost.deg]] <- data.table(
cost.param, degree.num, boundaries)
}
subtrain.dt[, alpha := 0]
train.row.vec <- as.integer(rownames(xmatrix(fit)[[1]]))
subtrain.dt[train.row.vec, alpha := kernlab::alpha(fit)[[1]] ]
subtrain.dt[, status := ifelse(
alpha==0, "alpha=0",
ifelse(alpha==cost.param, "alpha=C", "0<alpha<C"))]
predictions.list[[paste(cost.param, degree.num)]] <- data.table(
cost.param, degree.num, subtrain.dt)
}
}
inputBoundaries <- do.call(rbind, inputBoundaries.list)
predictions <- do.call(rbind, predictions.list)
setErrors <- do.call(rbind, setErrors.list)
validationErrors <- setErrors[set=="validation"]
validationErrors$select <- "degree"
setErrors$select <- "cost"
animint(
selectModel=ggplot()+
ggtitle("Select hyper parameters")+
geom_tallrect(aes(
xmin=log10(cost.param)-cost.by/2,
xmax=log10(cost.param)+cost.by/2),
clickSelects="cost.param",
alpha=0.5,
data=setErrors[degree.num==1 & set=="subtrain",])+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
theme_animint(width=350, rowspan=1)+
facet_grid(select ~ ., scales="free")+
ylab("")+
geom_line(aes(
log10(cost.param), errors,
key=set,
group=set,
color=set),
showSelected="degree.num",
data=setErrors)+
scale_fill_gradient("validErr", low="white", high="red")+
geom_tile(aes(
log10(cost.param), degree.num, fill=errors),
clickSelects="degree.num",
data=validationErrors),
inputSpace=ggplot()+
theme_bw()+
ggtitle("Espace des fonctionnalités d'entrée")+
scale_fill_manual(values=sv.colors, breaks=names(sv.colors))+
geom_vline(aes(
xintercept=boundary),
color="violet",
data=x1.boundaries)+
scale_linetype_manual(values=c(
margin="dashed",
decision="solid"))+
geom_path(aes(
x1, x2,
group=path.i,
linetype=boundary),
showSelected=c("degree.num", "cost.param"),
color="black",
data=inputBoundaries)+
geom_point(aes(
x1, x2, color=y, fill=status),
showSelected=c("cost.param", "degree.num"),
size=3,
data=predictions))
```
<!-- paragraph -->
## Résumé du chapitre et exercices {#Ch12-exercises}
<!-- paragraph -->
Nous avons utilisé des `ggplots` pour visualiser le modèle de séparateur à vaste marge pour la classification binaire.
<!-- comment -->
Nous avons utilisé `animint()` et l'interactivité pour montrer comment la limite de décision du SVM varie en fonction des hyperparamètres du modèle.
<!-- paragraph -->
Exercices :
<!-- paragraph -->
- Utilisez [la mise en page d'un tableau HTML](../ch06/ch06-other#html-table-layout) pour [`viz.linear.svm`](#linear-svm) de manière à ce que les deux graphiques de l'espace des fonctionnalités apparaissent l'un à côté de l'autre et que le graphique "Select regularization parameter" apparaisse au-dessus ou en-dessous.
<!-- comment -->
- Utilisez `rbfdot` comme fonction noyau.
<!-- comment -->
Calculez l'erreur de sous-entraînement et de validation, puis ajoutez un nouveau panneau au graphique "select hyper parameters".
<!-- comment -->
- Les échelles par défaut utilisent les deux mêmes couleurs pour les légendes **y** et **set**, ce qui peut prêter à confusion.
<!-- comment -->
Modifiez les couleurs de l'une des deux légendes pour qu'elles soient différentes.
<!-- comment -->
- Utilisez les paramètres `color` et `color_off` pour modifier l'apparence de `geom_tile` selon s'il est sélectionné ou non, comme expliqué dans le [chapitre 6, à la section Préciser le mode d'affichage de l'état de la sélection](../Ch06/Ch06-other.html#display-selection-state).
<!-- paragraph -->
Dans le [chapitre 13](../Ch13/Ch13-poisson-regression.html), nous expliquerons comment visualiser le modèle de régression de Poisson.
<!-- paragraph -->