# Probabilités critiques (valeurs p)
<!-- paragraph -->
```{r setup, echo=FALSE}
knitr::opts_chunk$set(fig.path="ch19-figures/")
if(FALSE){
knitr::knit("index.qmd")
}
```
<!-- paragraph -->
Dans ce chapitre, nous allons explorer plusieurs visualisations des tests statistiques.
Plus précisement, nous allons visualiser la probabilité critique, aussi appelée la [valeur-p](https://fr.wikipedia.org/wiki/Valeur_p):
<!-- paragraph -->
- nous commençons par expliquer le concept de valeur-p.
<!-- comment -->
- nous simulons des données pour un test T à deux échantillons.
<!-- comment -->
- nous montrons comment créer un graphique en forme de volcan pour résumer un ensemble de valeurs-p.
<!-- comment -->
- nous expliquons comment l’occlusion pourrait être problèmatique dans un graphique avec trop de points, et comment contourner ce problème avec une carte thermique liée à un graphique montrant un sous-ensemble de points.
<!-- comment -->
- nous terminons par une autre carte thermique des valeurs des paramètres simulés, avec un graphique lié qui montre les données simulées.
<!-- paragraph -->
## Qu’est-ce qu’une valeur-p ?
<!-- comment -->
{#what-is-p-value}
<!-- paragraph -->
Une valeur P est utilisée pour mesurer la signification d’un test statistique.
<!-- comment -->
Les probabilités critiques (valeurs p) peuvent être calculées pour n’importe quel test statistique, mais une application typique est un test de Student entre deux conditions :
<!-- paragraph -->
- dans une expérience médicale, le traitement est-il plus efficace que le contrôle ?
<!-- comment -->
Par exemple, dans le cas d’un médicament pour la perte de poids, nous aimerions savoir si le poids du groupe expérimental est significativement inférieur à celui du groupe témoin.
<!-- comment -->
Supposons que 10 personnes soient assignées au groupe de contrôle et 15 au groupe de traitement.
<!-- comment -->
Nous pourrions ensuite calculer une valeur-p à l’aide d’un test de Student unilatéral pour évaluer la signification statistique (et non apparié parce que chaque personne du groupe de traitement n’a pas de membre correspondant dans le groupe témoin).
<!-- comment -->
- Dans une expérience d’apprentissage automatique, le réseau neuronal est-il plus précis que le modèle linéaire ?
<!-- comment -->
Par exemple, considérons un ensemble de données de référence de classification d’images, et une évaluation utilisant la validation croisée à 5 divisions.
<!-- comment -->
Nous aurions cinq mesures du taux d’erreur pour chacun des deux algorithmes d’apprentissage (réseau neuronal et modèle linéaire).
<!-- comment -->
Nous pourrions ensuite calculer une valeur-p à l’aide d’un test de Student unilatéral, pour évaluer la signification statistique (apparié parce qu’il y a un taux d’erreur pour chacun des algorithmes, dans chaque division de la validation croisée)
<!-- paragraph -->
Après avoir calculé les mesures (poids de chaque personne ou précision des tests de chaque algorithme d’apprentissage automatique), nous pouvons les utiliser comme données d’entrée pour `t.test()` qui calculera une valeur-p (plus elle est petite, plus la différence est significative).
<!-- comment -->
Pour comprendre la valeur-p, nous devons d’abord adopter l’hypothèse nulle : nous supposons qu’il n’y a pas de différence entre les conditions.
<!-- comment -->
Ensuite, la valeur-p du test est définie comme la probabilité que nous observions une différence aussi grande que les mesures données, ou plus grande.
<!-- comment -->
Étant donné que l’hypothèse nulle est qu’il n’y a pas de différence, il est extrêmement improbable d’observer des différences importantes, c’est pourquoi les petites valeurs-p sont plus significatives.
<!-- paragraph -->
## Données simulées {#p-value-simulated-data}
<!-- paragraph -->
Nous commençons par simuler des données à utiliser avec `t.test()`.
<!-- comment -->
Notre simulation comporte quatre paramètres :
<!-- paragraph -->
- `true_offset` est la véritable différence entre les conditions,
- `sd` est l’écart-type des données simulées,
- `sample` est un nombre d’échantillons (la moitié des échantillons dans une condition, l’autre moitié dans l’autre condition),
- `trial` est le nombre de fois que nous répétons l’expérience (pour chaque différence et écart-type).
<!-- paragraph -->
Le code ci-dessous utilise `CJ()` pour définir les valeurs de chaque paramètre :
<!-- paragraph -->
```{r}
library(data.table)
offset_by <- 0.1
sd_by <- 0.1
set.seed(1)
(sim_dt <- CJ(
true_offset=round(
seq(-3, 3, by=offset_by),
ceiling(-log10(offset_by))),
sd=seq(0.1, 1, by=sd_by),
sample=seq(0, 9),
trial=seq_len(100)
)[, let(
condition = sample %% 2,
pair = sample %/% 2
)][, let(
value = rnorm(.N, true_offset*condition, sd)
)][])
```
<!-- paragraph -->
Le résultat ci-dessus montre plusieurs centaines de milliers de lignes, une pour chaque `value` (valeur) normale aléatoire simulée (dont la moyenne dépend de `true_offset` et de `condition`).
<!-- paragraph -->
## Test de Student et graphique volcan {#t-test-and-volcano-plot}
<!-- paragraph -->
Dans cette section, nous calculons les résultats des tests t et les visualisons à l’aide d’un graphique volcan, qui est un graphique des valeurs-p en logarithme négatif par rapport aux tailles d’effet estimées.
<!-- comment -->
La visualisation des résultats du test est appelée graphique volcan parce que la distribution typique des points ressemble à un volcan en éruption de l’origine vers le haut, vers la gauche et vers la droite.
<!-- -- commentaire -->
Tout d’abord, nous ajoutons les colonnes que nous utiliserons pour la visualisation :
<!-- paragraph -->
- `true_tile` est une chaîne de texte permettant de sélectionner une combinaison d’une différence et d’un écart-type.
<!-- comment -->
- `Condition` est une chaîne de caractères indiquant la condition (soit `zero` ou `offset`).
<!-- paragraph -->
```{r}
sim_dt[, let(
true_tile=paste(true_offset, sd),
Condition = ifelse(condition, "offset", "zero")
)]
```
<!-- paragraph -->
Ensuite, nous effectuons un remodelage pour obtenir un tableau avec une colonne pour chaque condition (`zero` et `offset`).
<!-- paragraph -->
```{r}
(sim_wide <- dcast(
sim_dt,
true_tile + true_offset + sd + trial + pair ~ Condition))
```
<!-- paragraph -->
La sortie ci-dessus montre un tableau comportant deux fois moins de lignes que le tableau précédent.
<!-- comment -->
Le code ci-dessous calcule un test de Student pour chaque répétition de la simulation :
<!-- paragraph -->
```{r}
(sim_p <- sim_wide[, {
t.result <- t.test(zero, offset, var.equal=TRUE)
with(t.result, data.table(
p.value,
mean_zero=estimate[1],
mean_offset=estimate[2]
))
}, by=.(true_tile, true_offset, sd, trial)])
```
<!-- paragraph -->
La sortie ci-dessus comporte une ligne pour chaque test de Student et des colonnes pour la différence moyenne (`mean_zero`) et la `p.value`.
<!-- comment -->
Comme il y a dix échantillons par essai, il y a dix fois moins de lignes que dans le tableau de données simulées original.
<!-- comment -->
Chaque essai implique un test de Student avec 5 échantillons dans le groupe témoin (`condition=zero`), contre 5 échantillons dans le groupe expérimentale (`condition=offset`).
<!-- comment -->
Ensuite, nous ajoutons des colonnes pour le graphique volcan :
<!-- paragraph -->
- `diff_means` est la différence entre les moyennes des deux conditions, parfois appelée « taille de l’effet ».
- `neg.log10.p` est la probabilté critique, transformée en logarithme négatif (plus elle est grande, plus elle est significative).
<!-- paragraph -->
```{r}
sim_p[, let(
diff_means = mean_offset - mean_zero,
neg.log10.p = -log10(p.value)
)]
```
<!-- paragraph -->
Ensuite, nous dessinons le graphique volcan :
<!-- paragraph -->
- L’axe des X indique la différence entre les conditions (taille de l’effet).
<!-- comment -->
- L’axe des Y indique le logarithme négatif de la valeur P.
<!-- paragraph -->
```{r}
library(animint2)
(gg.volcano <- ggplot()+
geom_point(aes(
diff_means, neg.log10.p, fill=true_offset, color=sd),
data=sim_p)+
scale_fill_gradient2()+
scale_color_gradient(low="white", high="black")+
theme_bw())
```
<!-- paragraph -->
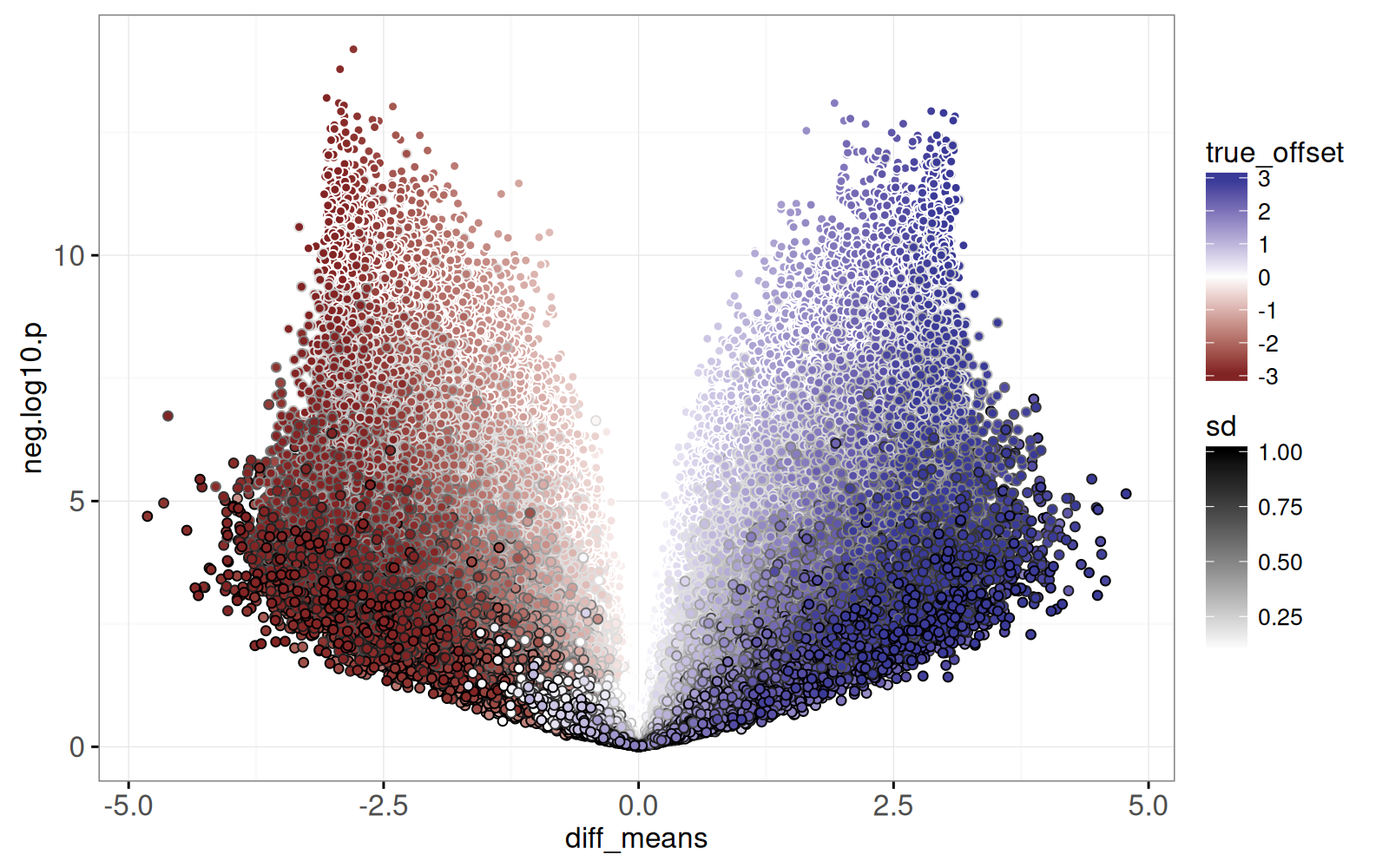
Le graphique statique ci-dessus montre un point par résultat de test de Student.
<!-- comment -->
Les points proches de l’origine (0,0) représentent des tests qui n’ont pas produit de différence significative, tandis que les points avec de grandes valeurs Y représentent des différences significatives.
<!-- comment -->
Il comprend également `fill=true_offset` et `color=sd` afin que nous puissions voir comment les paramètres de simulation affectent le graphique volcan :
<!-- paragraph -->
- Les valeurs de `sd` plus grandes apparaissent en bas (plus il y a de variance, plus il est difficile de détecter une différence).
<!-- comment -->
- Les couleurs plus foncées apparaissent près des bords gauche/droit (des décalages réels plus importants tendent à se traduire par des différences de moyennes calculées plus grandes).
<!-- paragraph -->
Enfin, on voit l’occlusion dans le nuage de points, ce qui signifie que nous ne pouvons pas voir tous les détails, car il y a trop de points de données tracés les uns sur les autres.
<!-- paragraph -->
## Corriger le surdimensionnement par la carte thermique et le zoom {#fix-overplotting-heatmap-zoom}
<!-- paragraph -->
Dans cette section, nous montrons comment le graphique volcan précédent peut être révisé pour montrer plus de détails, en utilisant une carte thermique liée à un nuage de points zoomé.
<!-- comment -->
Pour commencer, nous définissons la fonction `round_rel()` ci-dessous, qui est utilisée pour ajouter les colonnes `round_*` et `rel_*` que nous utiliserons pour définir les tuiles de la carte thermique.
<!-- paragraph -->
- les colonnes `round_*` sont arrondies à la taille de bac la plus proche (entière par défaut), et sont utilisées pour définir les positions `x` et `y` de la tuile de la carte thermique.
<!-- comment -->
- les colonnes `rel_*` sont utilisées pour les positions `x` et `y` dans l’affichage zoomé, et sont des unités relatives à la valeur de `round_*` correspondante.
<!-- paragraph -->
```{r}
round_rel <- function(DT, col_name, bin_size=1, offset=0){
value <- DT[[col_name]]
round_value <- round((value+offset)/bin_size)*bin_size
DT[, paste0(c("round","rel"), "_", col_name) := list(
round_value, value-round_value)]
}
round_rel(sim_p, "diff_means")
round_rel(sim_p, "neg.log10.p")
```
<!-- paragraph -->
Ensuite, nous définissons `volcano_tile` une combinaison de chaînes de texte de variables `round_*` qui sera utilisée pour la sélection.
<!-- paragraph -->
```{r}
sim_p[, volcano_tile := paste(round_diff_means, round_neg.log10.p)]
```
<!-- paragraph -->
Ensuite, nous calculons un tableau de contingence avec une ligne par carreau de la carte thermique que nous allons afficher.
<!-- paragraph -->
```{r}
(volcano_tile_dt <- sim_p[, .(
tests=.N
), by=.(volcano_tile, round_diff_means, round_neg.log10.p)])
```
<!-- paragraph -->
La sortie ci-dessus montre une ligne par tuile de la carte thermique, avec la colonne `tests` qui indique le nombre de points apparaissant dans la zone correspondante du graphique volcan.
<!-- comment -->
Ci-dessous, nous créons la carte thermique du volcan.
<!-- paragraph -->
```{r}
(gg.volcano.tiles <- ggplot()+
geom_tile(aes(
round_diff_means, round_neg.log10.p, fill=log10(tests)),
color="grey",
data=volcano_tile_dt)+
scale_fill_gradient(low="white",high="black")+
theme_bw())
```
<!-- paragraph -->
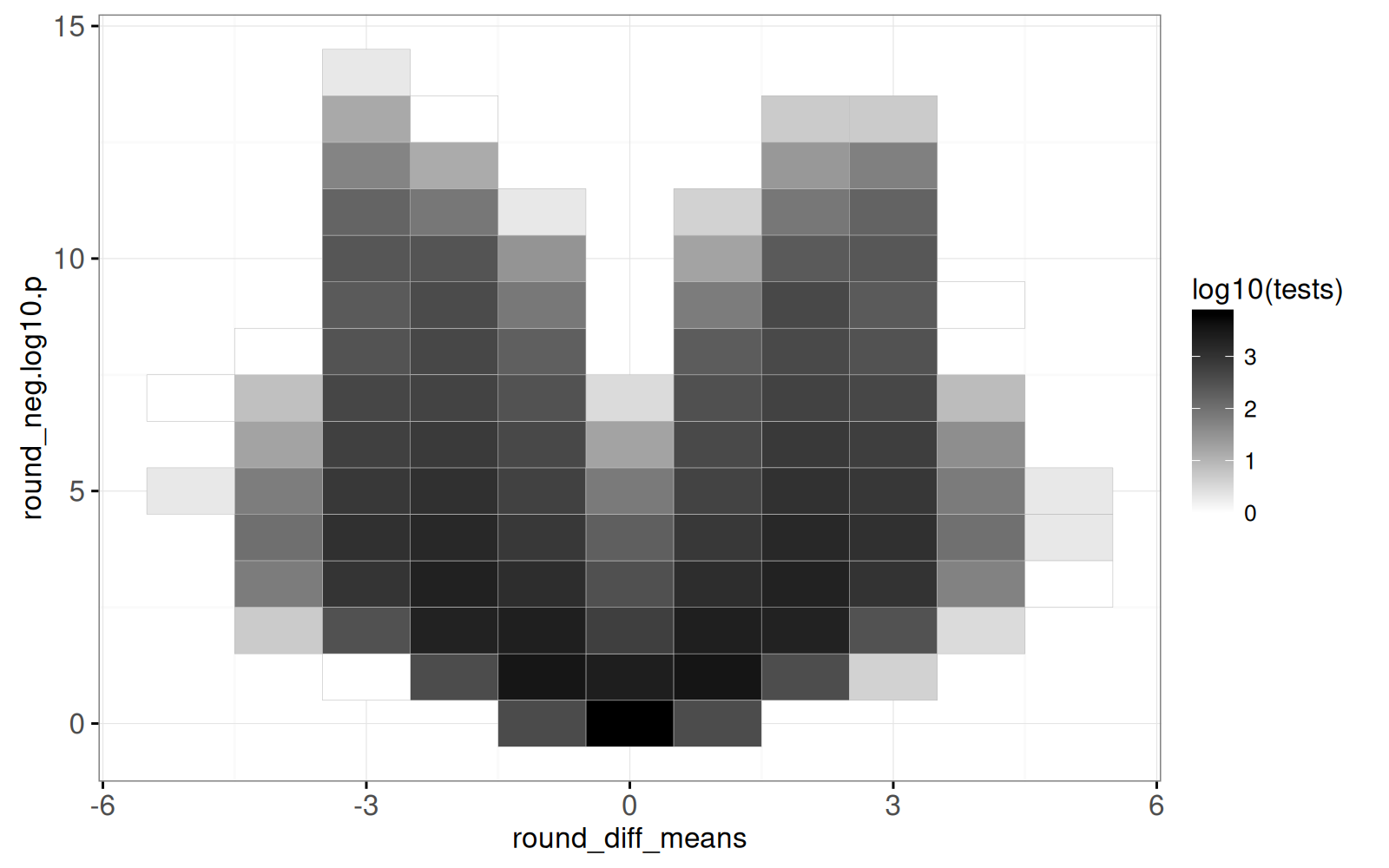
Le résultat ci-dessus est une carte thermique, les régions plus foncées indiquant les zones du graphique volcan qui ont plus de résultats de tests.
<!-- comment -->
Le code ci-dessous combine la carte thermique du volcan avec un nuage de points agrandi, en utilisant le sélecteur `volcano_tile` pour les relier.
<!-- paragraph -->
```{r ch19-vis-volcano}
(vis.volcano <- animint(
volcanoTiles=gg.volcano.tiles+
ggtitle("Click to select volcano tile")+
theme_animint(width=300, rowspan=1)+
geom_tile(aes(
round_diff_means, round_neg.log10.p),
clickSelects="volcano_tile",
color="green",
fill="transparent",
data=volcano_tile_dt),
volcanoZoom=ggplot()+
ggtitle("Zoom to selected volcano tile")+
geom_point(aes(
rel_diff_means, rel_neg.log10.p, fill=true_offset, color=sd),
showSelected="volcano_tile",
size=3,
data=sim_p)+
scale_fill_gradient2()+
scale_color_gradient(low="white", high="black")+
theme_bw()))
```
<!-- paragraph -->
Ci-dessus, après avoir cliqué sur la carte thermique de gauche, les données affichées dans le graphique de droite changent.
<!-- paragraph -->
## Visualisation d’une grille de simulations {#vis-grid-simulations}
<!-- paragraph -->
Dans cette section, nous créons une nouvelle visualisation pour révéler les détails de chaque combinaison de paramètres de simulation.
<!-- comment -->
Tout d’abord, dans le code ci-dessous, nous calculons la taille moyenne de l’effet (`diff_means`) et le logarithme négatif de la valeur P (`neg.log10.p`), sur l’ensemble des 100 répétitions de chaque combinaison de paramètres.
<!-- paragraph -->
```{r}
(sim_true_tiles <- dcast(
sim_p,
true_tile + true_offset + sd ~ .,
mean,
value.var=c("diff_means", "neg.log10.p")))
```
<!-- paragraph -->
Le résultat ci-dessus comporte une ligne par combinaison de paramètres de simulation (`true_offset` et `sd`).
<!-- comment -->
Nous utilisons le code ci-dessous pour visualiser cette grille de combinaisons de paramètres.
<!-- paragraph -->
```{r}
width <- offset_by*0.4
height <- sd_by*0.45
(gg.true.tiles <- ggplot()+
scale_x_continuous("True offset")+
scale_y_continuous("Standard deviation")+
scale_fill_gradient2(breaks=c(3,0,-3))+
scale_color_gradient(
guide=guide_legend(override.aes=list(fill='white')),
low="white", high="black", breaks=c(9,5,1))+
theme_bw()+
geom_rect(aes(
xmin=true_offset-width, xmax=true_offset+width,
ymin=sd-height, ymax=sd+height,
fill=diff_means, color=neg.log10.p),
data=sim_true_tiles))
```
<!-- paragraph -->
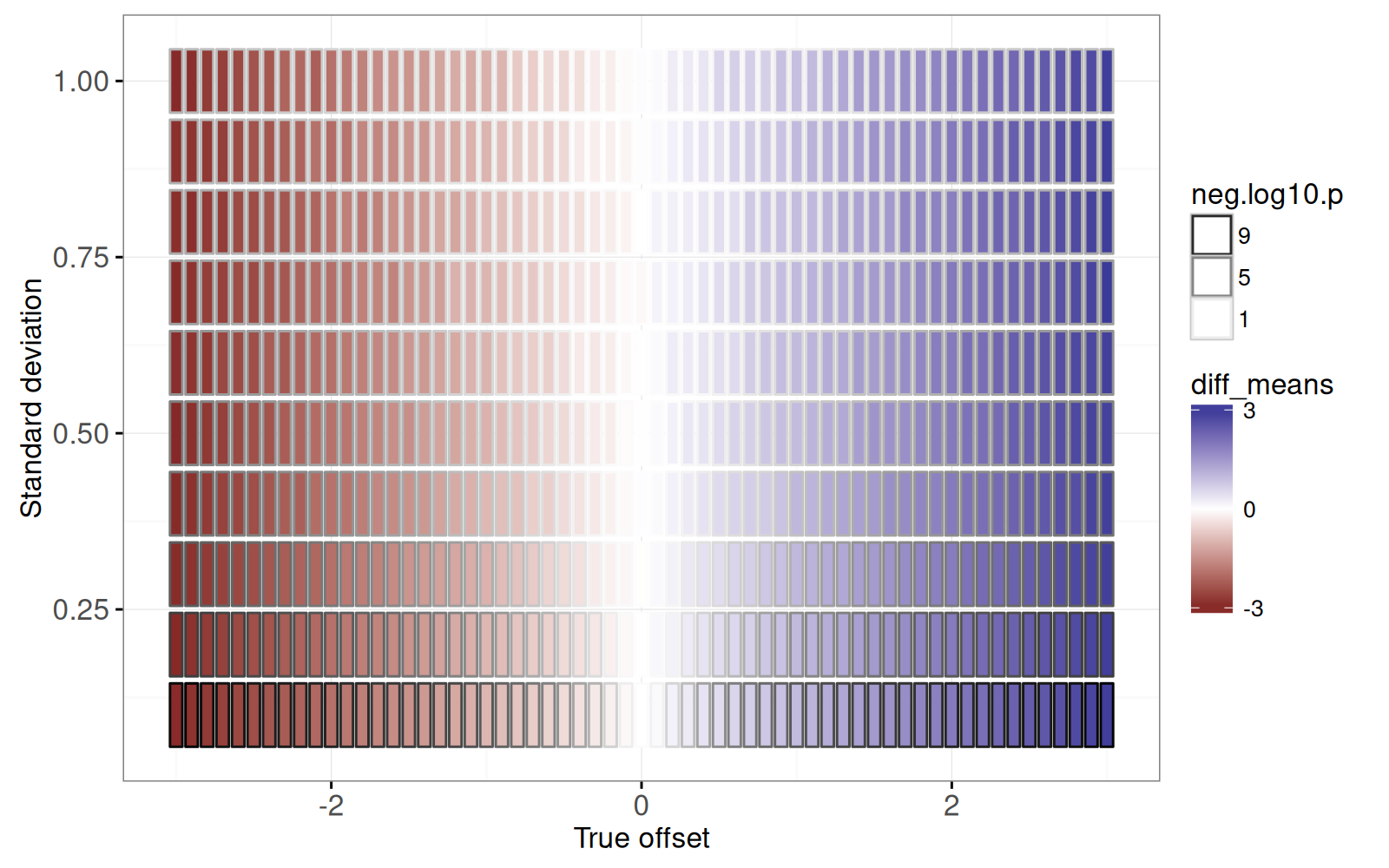
La figure ci-dessus montre un rectangle pour chaque combinaison de paramètres de simulation.
<!-- comment -->
Il est clair que :
<!-- paragraph -->
- la taille estimée de l’effet (`fill=diff_means`) est cohérente avec le décalage réel (axe des X).
<!-- comment -->
- les valeurs P les plus significatives (grandes `neg.log10.p`) sont associées à des paramètres à faible écart-type (parce que le rapport signal/bruit est plus important).
<!-- paragraph -->
Nous allons créer un graphique lié qui montre les détails des simulations pour chaque combinaison de paramètres.
<!-- comment -->
Nous commençons par établir le prototype des graphiques détaillés en examinant un sous-ensemble :
<!-- paragraph -->
```{r}
some <- function(DT)DT[true_offset %in% c(0,2) & sd == 1]
gg.true.tiles+
geom_rect(aes(
xmin=true_offset-width, xmax=true_offset+width,
ymin=sd-height, ymax=sd+height),
color="green",
fill=NA,
data=some(sim_true_tiles))
```
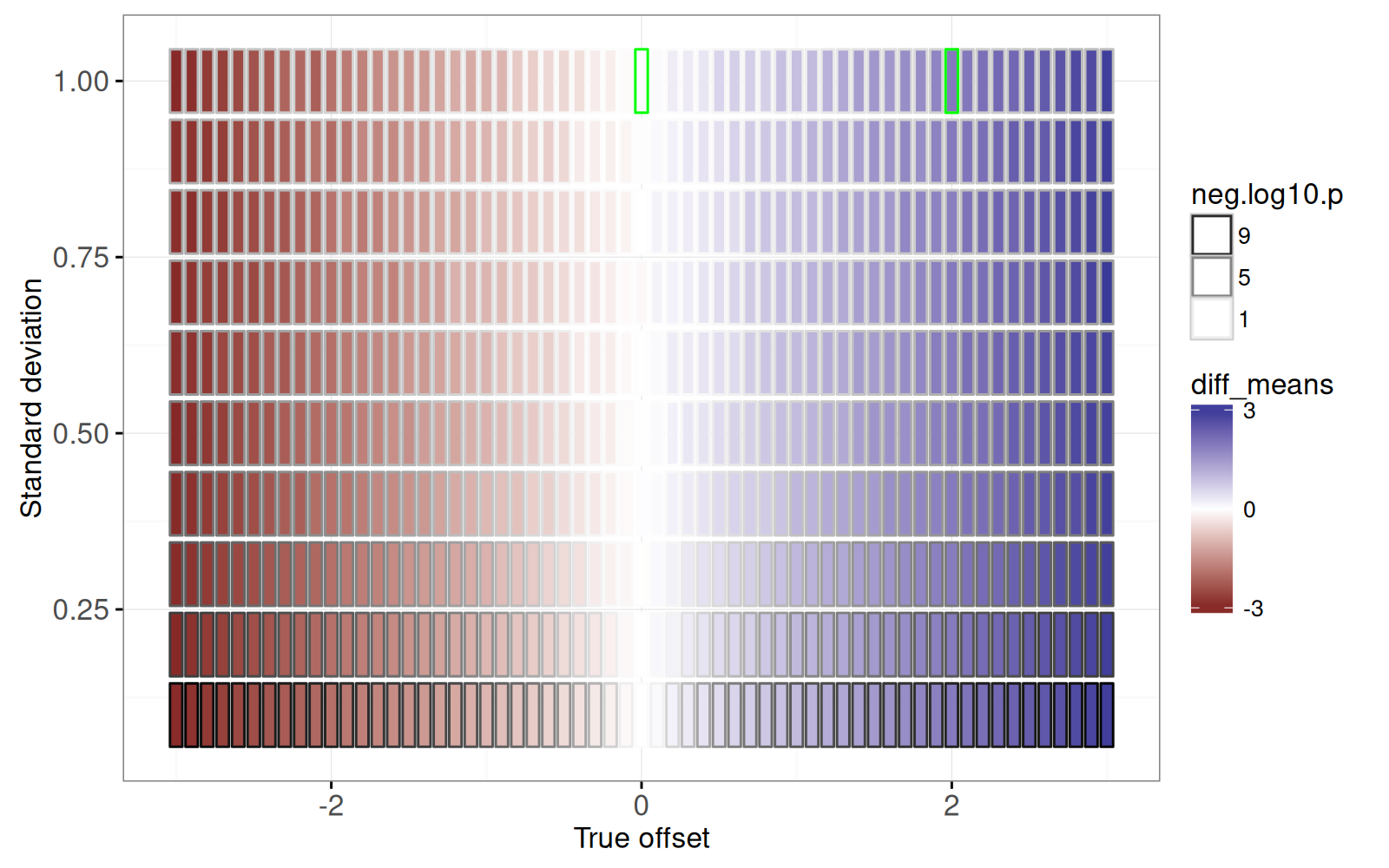
<!-- paragraph -->
La figure ci-dessus montre deux rectangles soulignés d’un contour vert, pour lesquels nous créons un graphique à facettes non interactif à l’aide du code ci-dessous.
<!-- paragraph -->
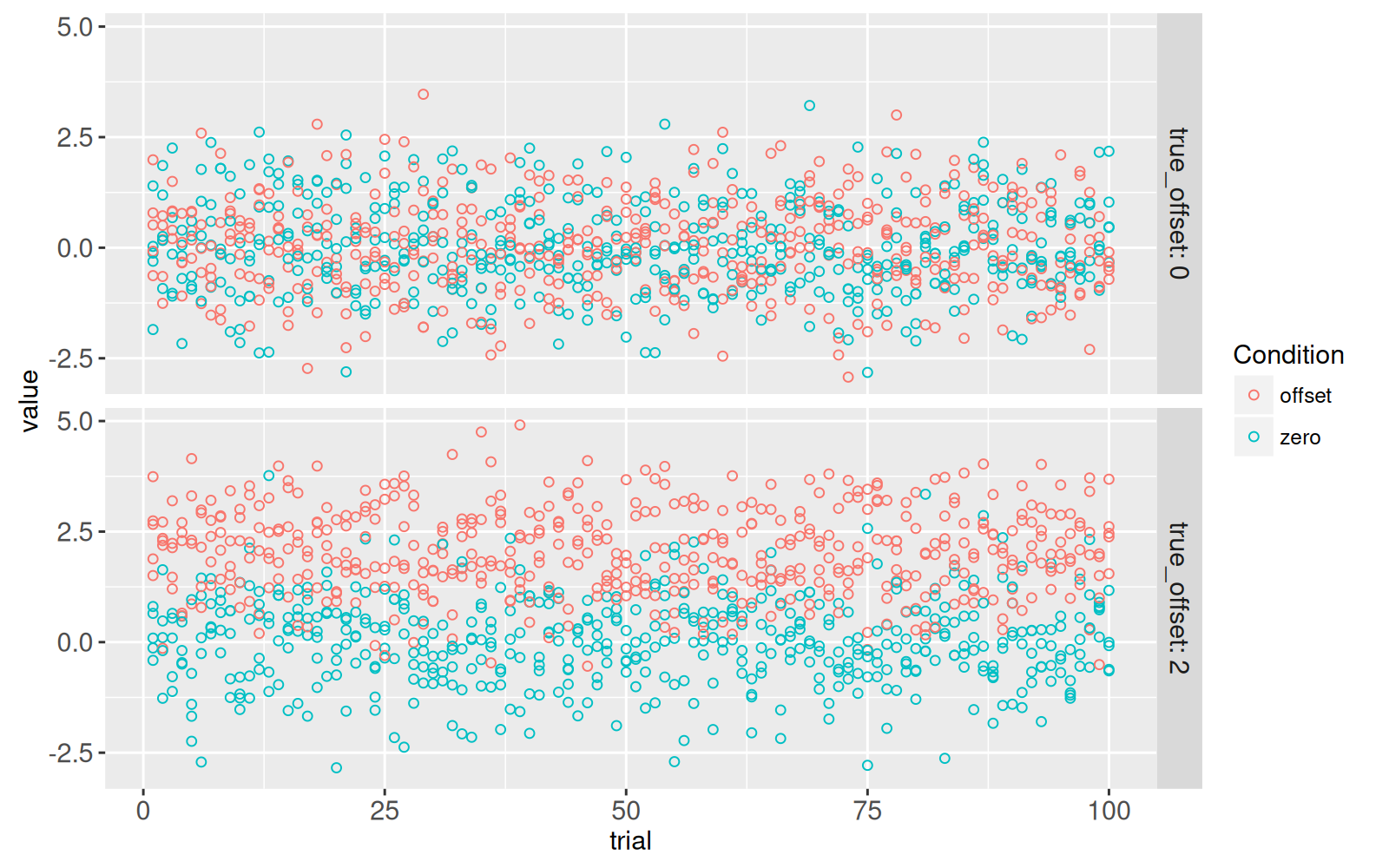
```{r}
(gg.some.values <- ggplot()+
facet_grid(true_offset ~ ., labeller=label_both)+
geom_point(aes(
trial, value, color=Condition),
data=some(sim_dt)))
```
<!-- paragraph -->
La figure ci-dessus montre un panneau pour chacune des deux combinaisons de paramètres mises en évidence dans le graphique précédent.
<!-- comment -->
L’axe des X représente `trial`, qui s’étend de 1 à 100, chacune avec différentes valeurs aléatoires simulées à l’aide des mêmes hypothèses (`true_offset=0` ou `2`).
<!-- comment -->
Le test de Student est utilisé pour déterminer s’il existe une différence de moyennes entre les deux conditions.
<!-- paragraph -->
- Quand `true_offset=0` il n’y a pas de différence entre les deux conditions, de sorte que le test de Student devrait avoir une petite taille d’effet et une grande probabilité critique.
<!-- comment -->
- Lorsque `true_offset=2` il y a une plus grande différence entre les deux conditions, de sorte que le test de Student devrait avoir une taille d’effet plus importante et une petite probabilité critique.
<!-- paragraph -->
Le code ci-dessous crée une nouvelle colonne `significant` qui indique si le test rejette l’hypothèse nulle au seuil traditionnel de 5 %.
<!-- paragraph -->
```{r}
sim_p[, significant := p.value < 0.05]
```
<!-- paragraph -->
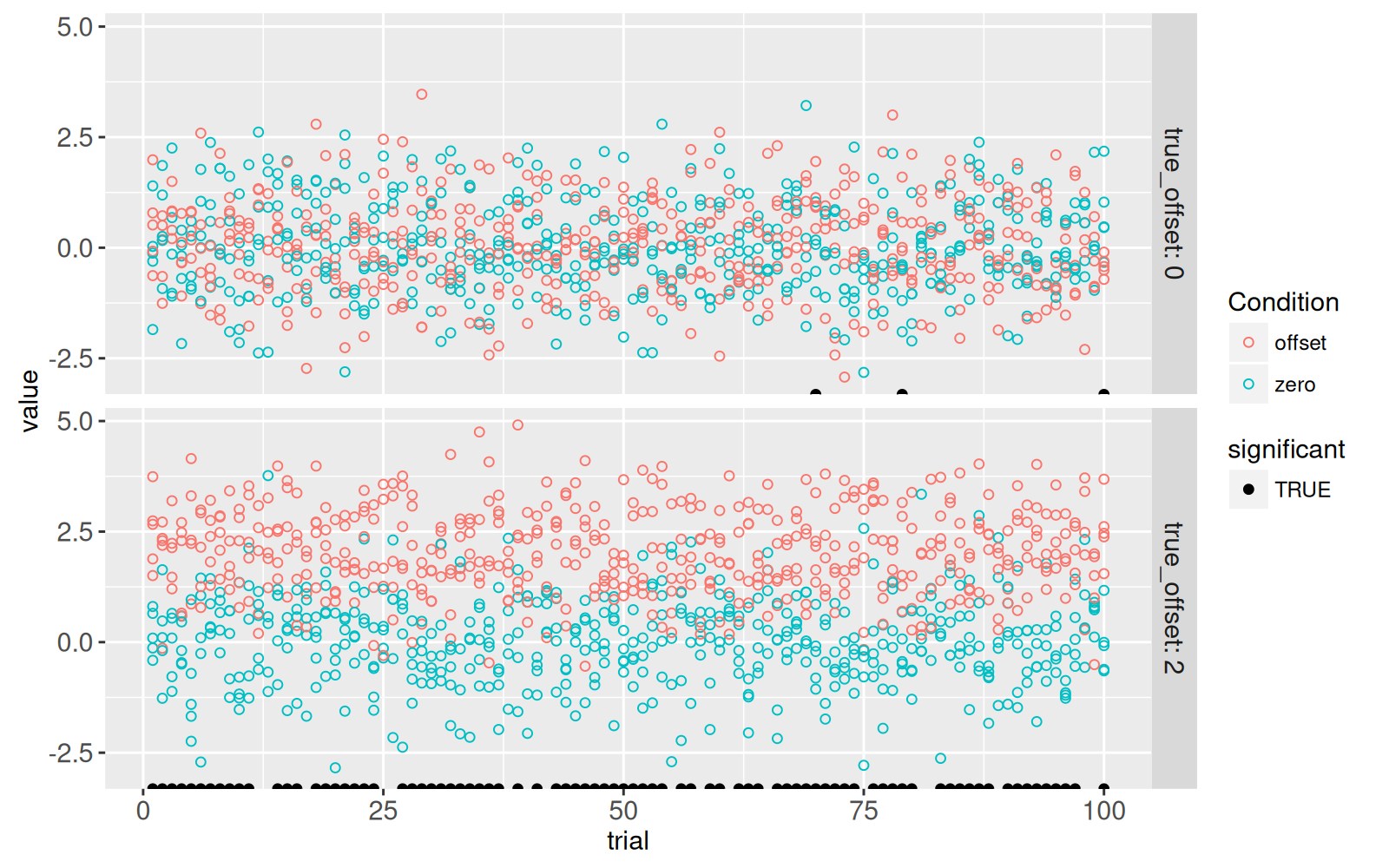
Le code ci-dessous ajoute un nouveau `geom_point()` pour mettre l’accent sur les essais qui ont montré une différence significative au niveau de 5 %.
<!-- paragraph -->
```{r}
only_significant <- sim_p[significant==TRUE]
gg.some.values+
geom_point(aes(
trial, -Inf, fill=significant),
data=some(only_significant))+
scale_fill_manual(values=c("TRUE"="black"))
```
<!-- paragraph -->
La figure ci-dessus montre un point noir pour chaque essai présentant une différence significative.
<!-- paragraph -->
- Pour `true_offset=0` nous voyons qu’il y a `r nrow(some(only_significant)[true_offset==0])` essais avec une différence significative, même s’il n’y a pas de différence dans les vraies moyennes dans la simulation.
<!-- comment -->
Ce nombre de faux positifs est cohérent avec le seuil de 5% de la valeur P (taux d’erreur de type I) que nous avons utilisé pour définir la significativité.
<!-- comment -->
- Pour `true_offset=2`, nous voyons que seul `r nrow(some(only_significant)[true_offset!=0])` des essais sont significatifs, même s’il y a une vraie différence de moyenne.
<!-- comment -->
La puissance estimée (taux de vrais positifs) est donc de `r some(sim_p)[true_offset!=0, paste0(100*mean(significant),"%")]` et le taux d’erreur de type II (taux de faux négatifs) est donc de `r some(sim_p)[true_offset!=0, paste0(100*mean(1-significant),"%")]`.
<!-- paragraph -->
Ci-dessous, nous créons une visualisation qui relie la carte thermique d’ensemble au graphique de dispersion détaillé, en remplaçant `facet_grid(true_offset ~ .)` dans le code ci-dessus par `showSelected="true_tile"` dans le code ci-dessous.
<!-- paragraph -->
```{r ch19-vis-true-tiles}
(vis.parameters <- animint(
tiles=gg.true.tiles+
ggtitle("Click to select simulation parameters")+
theme_animint(width=800, height=250, last_in_row=TRUE)+
geom_rect(aes(
xmin=true_offset-width, xmax=true_offset+width,
ymin=sd-height, ymax=sd+height),
fill="transparent",
color="green",
clickSelects="true_tile",
data=sim_true_tiles),
zoom=ggplot()+
ggtitle("Zoom to selected simulation parameters")+
theme_bw()+
theme_animint(width=800, height=300)+
geom_point(aes(
trial, value, color=Condition),
fill=NA,
showSelected="true_tile",
data=sim_dt)+
geom_point(aes(
trial, -Inf, fill=significant),
showSelected="true_tile",
data=only_significant)+
scale_fill_manual(values=c("TRUE"="black"))))
```
<!-- paragraph -->
Dans la visualisation ci-dessus, vous pouvez cliquer sur le graphique du haut pour sélectionner une combinaison de paramètres de simulation.
<!-- comment -->
Les 100 essais pour la combinaison de paramètres sélectionnée sont affichés dans le graphique du bas.
<!-- paragraph -->
## Résumé du chapitre et exercices {#ch19-exercises}
<!-- paragraph -->
Nous avons créé plusieurs visualisations des données à l’aide de simulations pour illustrer les valeurs P.
<!-- comment -->
Comme il y avait trop de tests t à montrer sur le graphique volcan, nous avons plutôt utilisé une carte thermique liée à un diagramme de dispersion zoomé.
<!-- comment -->
Nous avons également montré comment lier une carte thermique de combinaisons de paramètres à un graphique de dispersion qui montre les détails des valeurs correspondantes dans les simulations.
<!-- paragraph -->
Exercices :
<!-- paragraph -->
- Dans `vis.volcano`, en cliquant sur l’une des `volcanoTiles` du bas, on ne voit qu’une partie de l’espace occupé dans `volcanoZoom`.
<!-- comment -->
Pour corriger ce problème et occuper tout l’espace, revenez à la définition de `round_neg.log10.p` et utiliser l’argument `offset=0.5` dans `round_rel()` qui décale les valeurs relatives d’un certain décalage.
<!-- comment -->
- Dans `vis.volcano`, ajoutez `aes(tooltip)` à `volcanoTiles` pour indiquer le nombre de points dans chaque tuile de la carte thermique.
<!-- comment -->
- Notez que deux `geom_tile()` ont été utilisés dans `vis.volcano` et deux `geom_rect()` ont été utilisés dans `vis.parameters`.
<!-- comment -->
Le premier geom utilise la couleur et le remplissage pour visualiser les données, tandis que le second geom utilise `fill="transparent"` avec `color="green"` pour la sélection.
<!-- comment -->
Essayez une refonte avec un seul geom, qui n’utilise que des `aes(fill)` et utilise `color` comme paramètre de geom.
<!-- comment -->
Quels sont les inconvénients de l’approche utilisant un seul geom ?
<!-- comment -->
- Dans `vis.parameters`, ajoutez `geom_hline()` pour mettre en évidence la valeur sélectionnée du vrai décalage.
<!-- comment -->
- Dans `vis.parameters$zoom`, ajoutez `geom_segment()` pour représenter la différence entre les moyennes de chaque essai, en utilisant `aes(linetype=signficant)` pour montrer quelles différences sont significatives au seuil traditionnel de la valeur-p de `0.05`.
<!-- comment -->
- Dans `vis.parameters$zoom`, ajoutez `geom_point()` pour représenter la moyenne de chaque essai et de chaque condition.
<!-- comment -->
Conseil : vous pouvez soit ajouter deux instances de `geom_point()` ou une `geom_point()` avec un tableau de données plus long créé via `melt(sim_p, measure.vars=measure(Condition, sep="mean_(.*)"))`.
<!-- comment -->
- Ajoutez des éléments graphiques à `gg.volcano` pour mettre l’accent sur le seuil traditionnel de la valeur-p de `0.05` : `geom_hline()` peut montrer le seuil, et `geom_text()` peut indiquer combien de tests se situent au-dessus ou au-dessous du seuil (utiliser un texte comme « 1500 tests non significatifs »).
<!-- comment -->
- Ajoutez `aes(tooltip)` à `gg.true.tiles` pour afficher les valeurs de `neg.log10.p` et `diff_means`.
<!-- comment -->
- Ajoutez une animation à `vis.parameters` de manière à ce qu’une nouvelle combinaison de paramètres apparaisse toutes les secondes.
<!-- comment -->
- Ajoutez `first` à `vis.parameters` afin que la première sélection affichée corresponde à l’une des combinaisons de paramètres présentées dans le graphique statique à facettes.
<!-- comment -->
- Combinez `vis.volcano` avec `vis.parameters` pour créer une nouvelle visualisation des données avec quatre graphiques liés.
<!-- comment -->
Différents types d’interactions sont possibles : - Dans `volcanoZoom`, utilisez `clickSelects="true_tile"` pour que l’interactivité permette de mapper les points du graphique volcan dans l’espace des paramètres de simulation.
<!-- comment -->
Ajoutez des points verts avec `showSelected="true_tile"` à `volcanoTiles` pour montrer où les 100 essais pour la combinaison de paramètres sélectionnée apparaissent dans l’espace du graphique du volcan.
<!-- comment -->
- Créez une nouvelle variable de sélection qui est une combinaison unique de `true_tile` et `trial`, puis utilisez-la pour `clickSelects` dans les deux `volcanoZoom` et `vis.parameters$zoom` de sorte que nous pouvons voir une correspondance entre un point dans l’espace volcan et un essai dans le graphique des détails du zoom sur les paramètres.
<!-- paragraph -->
Ensuite, dans le [chapitre 20](/ch19), nous expliquons la visualisation des résultats d’apprentissage artificiel avec le package `mlr3`.
<!-- paragraph -->