# Détection supervisée des ruptures
<!-- paragraph -->
```{r setup, echo=FALSE}
knitr::opts_chunk$set(fig.path="ch16-figures/")
```
<!-- paragraph -->
Dans ce chapitre, nous allons explorer plusieurs visualisations des modèles de détection supervisée des ruptures, dans les données séquentielles.
<!-- paragraph -->
Plan du chapitre :
<!-- paragraph -->
- Nous commençons par effectuer plusieurs visualisations statiques du jeu de données `intreg`.
<!-- comment -->
- Nous créons ensuite une visualisation interactive dans laquelle un graphique peut être cliqué pour sélectionner le nombre de ruptures et segments, avec un autre graphique qui affiche le modèle correspondant.
<!-- comment -->
- Nous terminons en montrant une visualisation statique du modèle de régression linéaire de la marge maximale, et en suggérant des exercices pour créer une version interactive.
<!-- paragraph -->
## Figures statiques {#static-change-point}
<!-- paragraph -->
Nous commençons par charger le jeu de données `intreg`.
<!-- paragraph -->
```{r intreg}
library(animint2)
data(intreg)
library(data.table)
lapply(intreg, function(df)data.table(df)[1:2])
```
<!-- paragraph -->
Comme on peut voir ci-dessus, il s’agit d’une liste nommée de 7 `data.frames` apparentés.
<!-- comment -->
Nous commençons notre exploration de ces données en traçant les signaux dans des facettes séparées.
<!-- paragraph -->
```{r signals}
data.color <- "grey50"
gg.signals <- ggplot()+
theme_bw()+
facet_grid(signal ~ ., scales="free")+
geom_point(aes(
base/1e6, logratio,
showSelected="signal"),
color=data.color,
data=intreg$signals)
gg.signals
```
<!-- paragraph -->
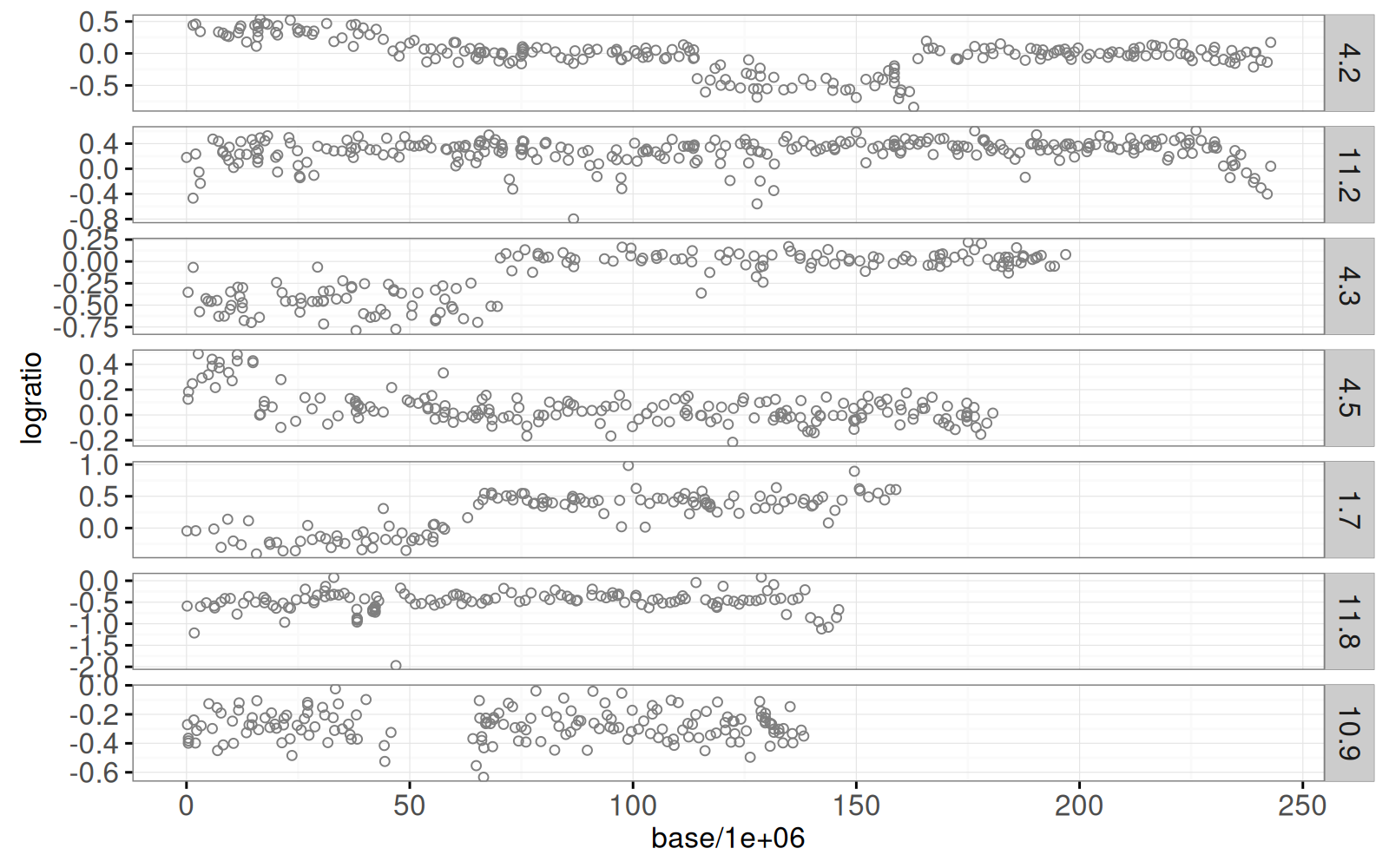
Chaque point de données tracé ci-dessus montre une mesure approximative du nombre de copies d’ADN (logratio), en fonction de la position des bases sur un chromosome.
<!-- comment -->
Ces données proviennent d’analyses à haut débit qui sont importantes pour diagnostiquer certains types de cancer comme le neuroblastome.
<!-- paragraph -->
Une partie importante du diagnostic consiste à détecter les points de rupture, soit les changements abrupts au sein d’un chromosome donné (panneau).
<!-- comment -->
Le graphique ci-dessus montre clairement qu’il y a plusieurs points de rupture dans ces données.
<!-- comment -->
En particulier, le signal 4.2 semble avoir trois points de rupture, le signal 4.3 semble en avoir un, etc.
<!-- comment -->
En fait, ces données proviennent de médecins de l’Institut Curie (Paris, France) qui ont annoté visuellement les régions avec et sans points de rupture.
<!-- comment -->
Ces données sont disponibles en tant que `intreg$annotations` et sont tracées ci-dessous.
<!-- paragraph -->
```{r annotations}
breakpoint.colors <- c(
"1breakpoint"="#ff7d7d",
"0breakpoints"='#f6f4bf')
gg.ann <- gg.signals+
scale_fill_manual(values=breakpoint.colors)+
geom_tallrect(aes(
xmin=first.base/1e6, xmax=last.base/1e6,
fill=annotation),
color="grey",
alpha=0.5,
data=intreg$annotations)
gg.ann
```
<!-- paragraph -->
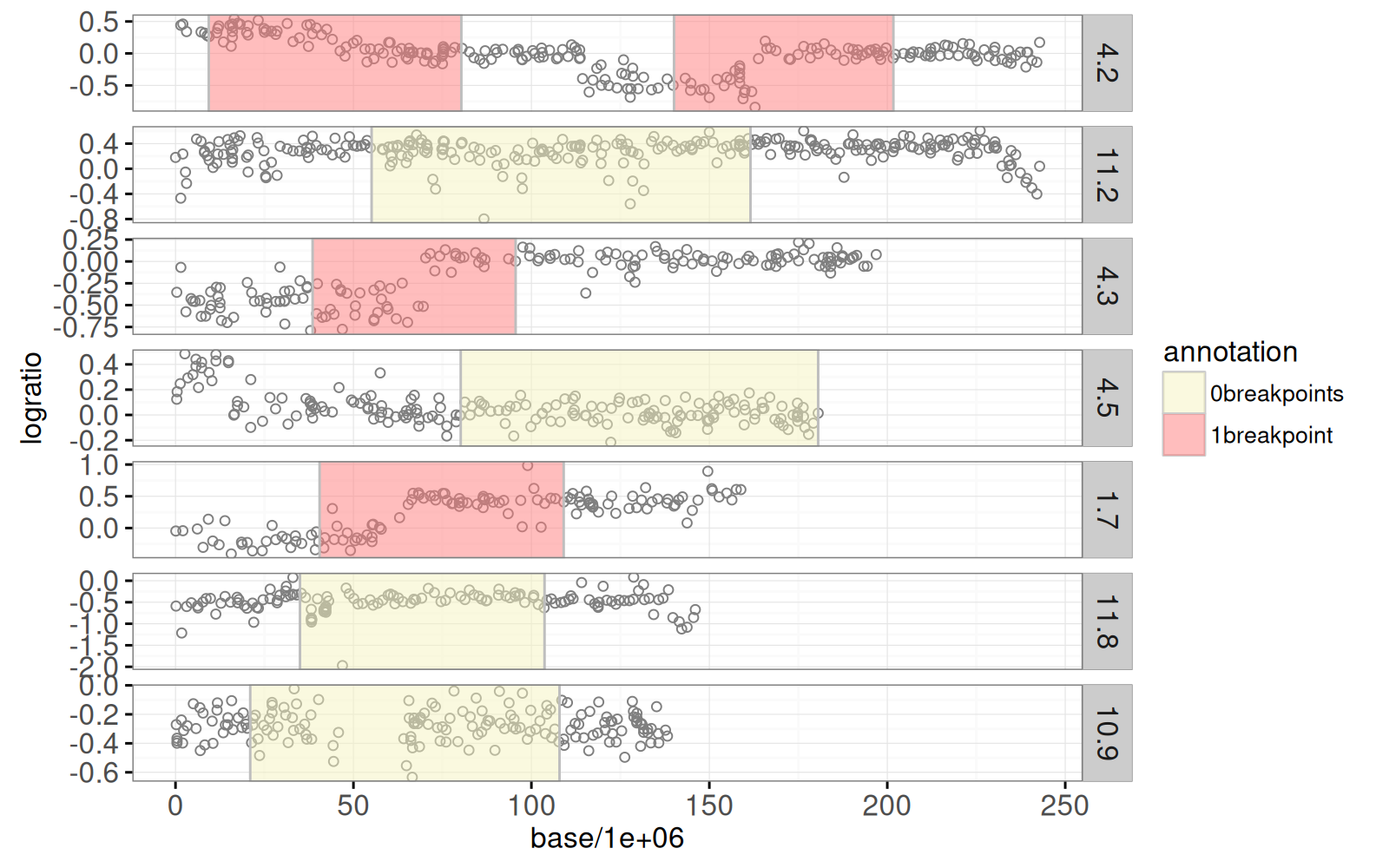
Le graphique ci-dessus montre en jaune les régions où les médecins ont déterminé qu’il n’y a pas de point de rupture significatif, et en rouge les régions où il y a un point de rupture.
<!-- comment -->
L’objectif de l’analyse de ces données est d’apprendre à partir des données étiquetées limitées (régions colorées) et de fournir des prédictions cohérentes sur les points de rupture (même dans les régions non étiquetées).
<!-- paragraph -->
Afin de détecter ces points de rupture, nous avons ajusté certains modèles de segmentation de vraisemblance maximale, en utilisant l'algorithme efficace implémenté dans `jointseg::Fpsn`.
<!-- comment -->
Les moyennes des segments sont disponibles dans `intreg$segments` et les points de rupture prédits sont disponibles dans `intreg$breaks`.
<!-- comment -->
Pour chaque signal, il existe une séquence de modèles de 1 à 20 segments.
<!-- comment -->
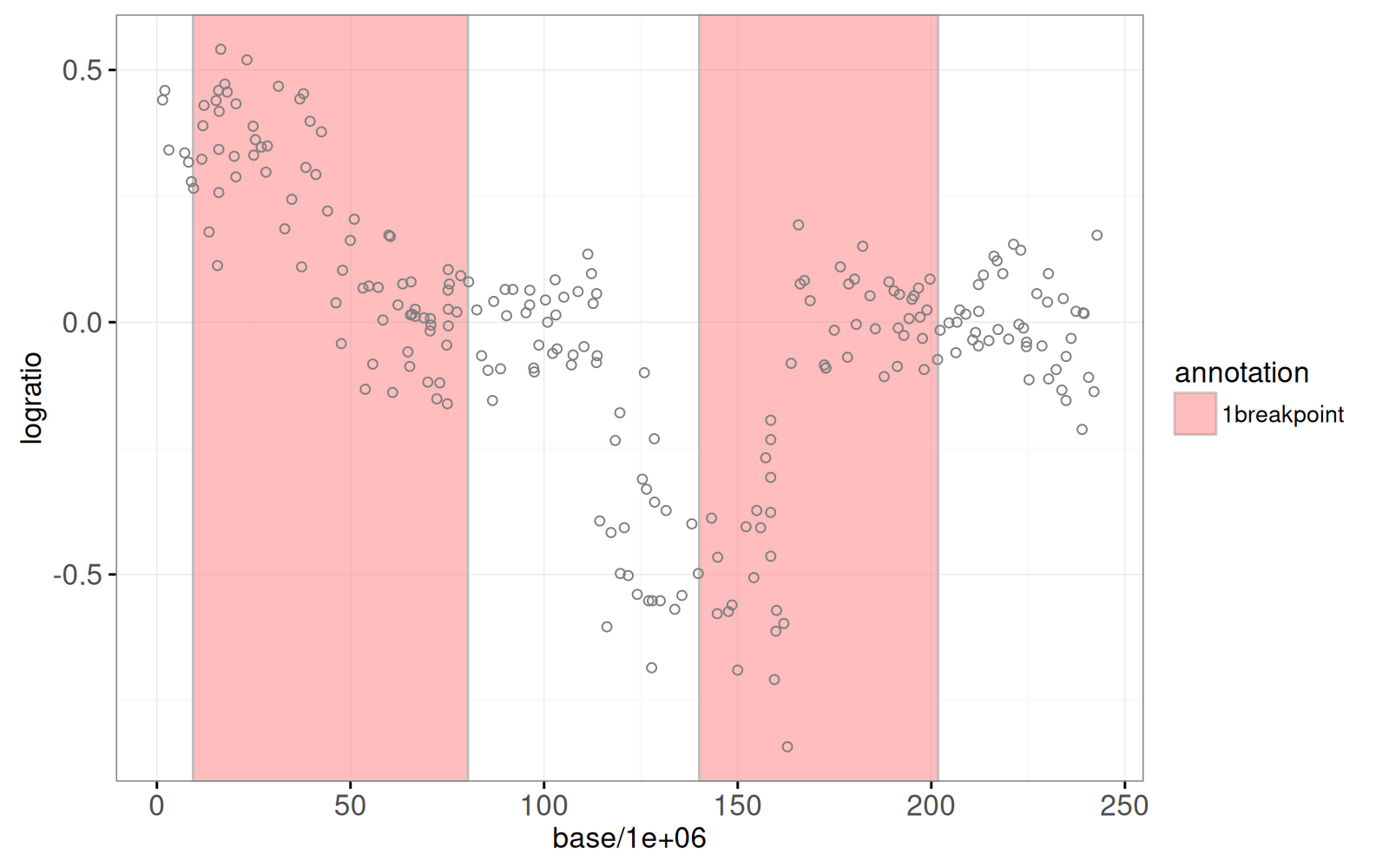
Zoomons d’abord sur un signal :
<!-- paragraph -->
```{r one}
sig.name <- "4.2"
show.segs <- 7
sig.labels <- subset(intreg$annotations, signal==sig.name)
gg.one <- ggplot()+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
geom_tallrect(aes(
xmin=first.base/1e6, xmax=last.base/1e6,
fill=annotation),
color="grey",
alpha=0.5,
data=sig.labels)+
geom_point(aes(
base/1e6, logratio),
color=data.color,
data=subset(intreg$signals, signal==sig.name))+
scale_fill_manual(values=breakpoint.colors)
gg.one
```
<!-- paragraph -->
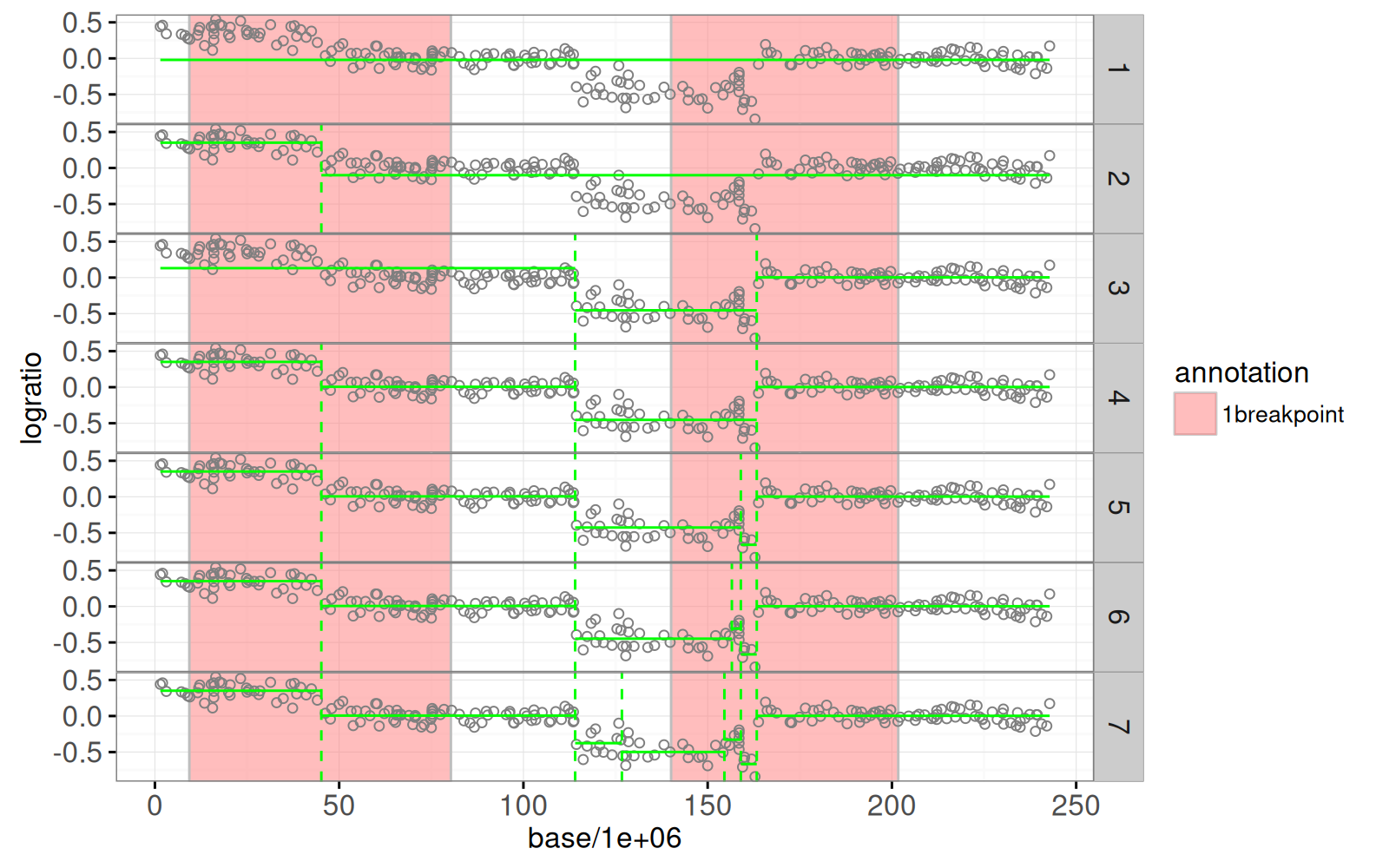
Nous traçons ci-dessous certains de ces modèles pour l’un des signaux :
<!-- paragraph -->
```{r models}
sig.segs <- data.table(
intreg$segments)[signal == sig.name & segments <= show.segs]
sig.breaks <- data.table(
intreg$breaks)[signal == sig.name & segments <= show.segs]
model.color <- "green"
gg.models <- gg.one+
facet_grid(segments ~ .)+
geom_segment(aes(
first.base/1e6, mean,
xend=last.base/1e6, yend=mean),
color=model.color,
data=sig.segs)+
geom_vline(aes(
xintercept=base/1e6),
color=model.color,
linetype="dashed",
data=sig.breaks)
gg.models
```
<!-- paragraph -->
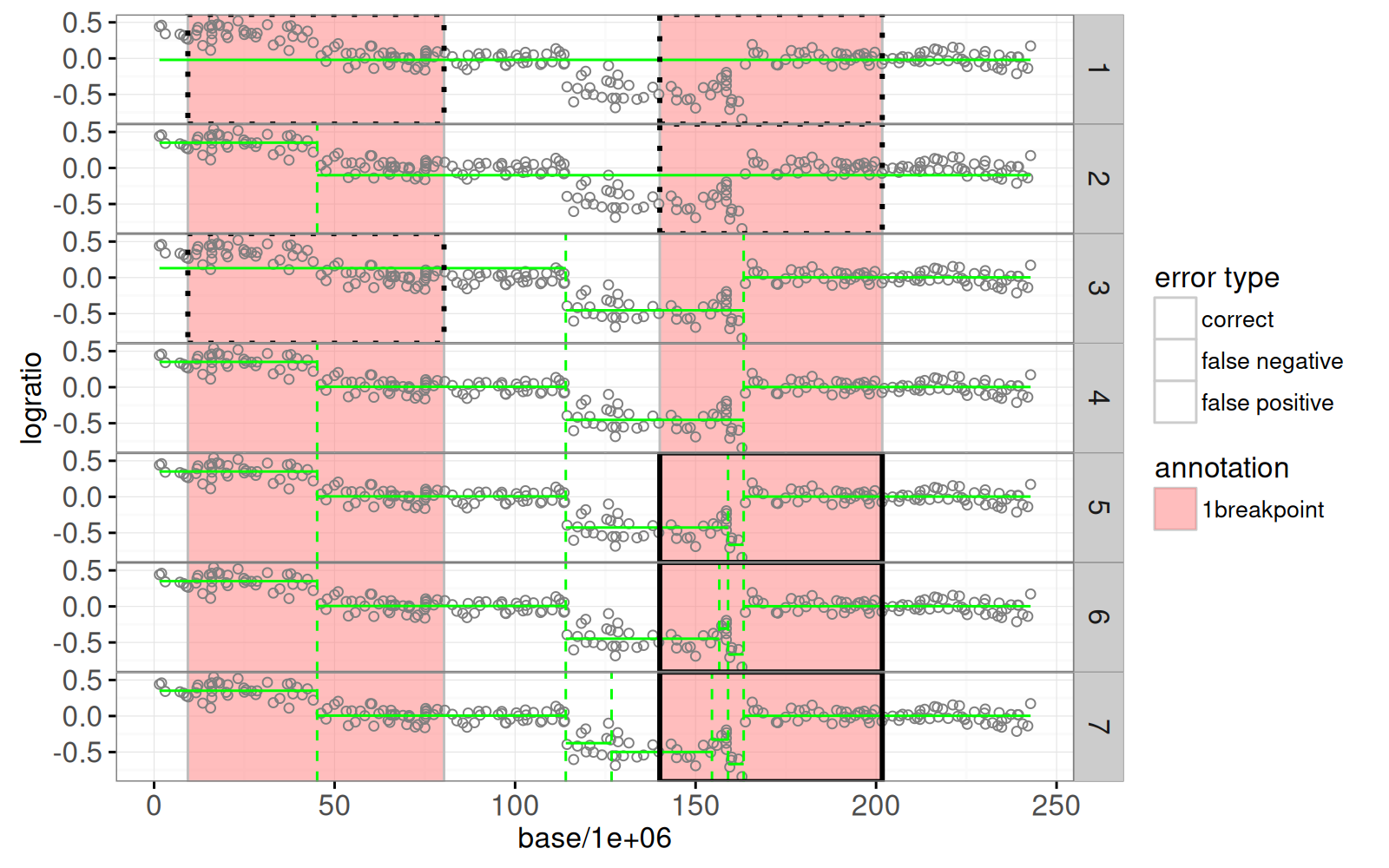
Le graphique ci-dessus montre les modèles de segmentation de vraisemblance maximale en vert (de un à six segments).
<!-- comment -->
Ci-dessous, nous utilisons la fonction `penaltyLearning::labelError` pour calculer l'erreur d'étiquette, qui quantifie quels modèles sont en accord avec quelles étiquettes.
<!-- paragraph -->
```{r labelerr}
sig.models <- data.table(segments=1:show.segs, signal=sig.name)
sig.errors <- penaltyLearning::labelError(
sig.models, sig.labels, sig.breaks,
change.var="base",
label.vars=c("first.base", "last.base"),
model.vars="segments",
problem.vars="signal")
```
<!-- paragraph -->
Le `data.table` (tableau de données) `sig.errors$label.errors` contient une ligne pour chaque combinaison (modèle, étiquette).
<!-- comment -->
La colonne `status` peut être utilisée pour afficher l’erreur d’étiquette : `false negative` pour trop peu de ruptures, `false positive` pour trop de ruptures, ou `correct` pour le bon nombre de modifications.
<!-- paragraph -->
```{r plotlabelerr}
gg.models+
geom_tallrect(aes(
xmin=first.base/1e6, xmax=last.base/1e6,
linetype=status),
data=sig.errors$label.errors,
color="black",
size=1,
fill=NA)+
scale_linetype_manual(
"type d'erreur",
values=c(
correct=0,
"false negative"=3,
"false positive"=1))
```
<!-- paragraph -->
En examinant le graphique des erreurs d’étiquettes ci-dessus, il est clair que le modèle à quatre segments devrait être sélectionné, car il permet d’obtenir des erreurs d’étiquettes nulles.
<!-- comment -->
Un certain nombre de critères peuvent être utilisés pour sélectionner le meilleur modèle.
<!-- comment -->
Une façon d’y parvenir est de sélectionner le modèle avec $s$ segments est $S^*(\lambda)=L_s + \lambda*s$, où $L_s$ est la perte totale du modèle avec $s$ segments, et $\lambda$ est une pénalité non négative.
<!-- comment -->
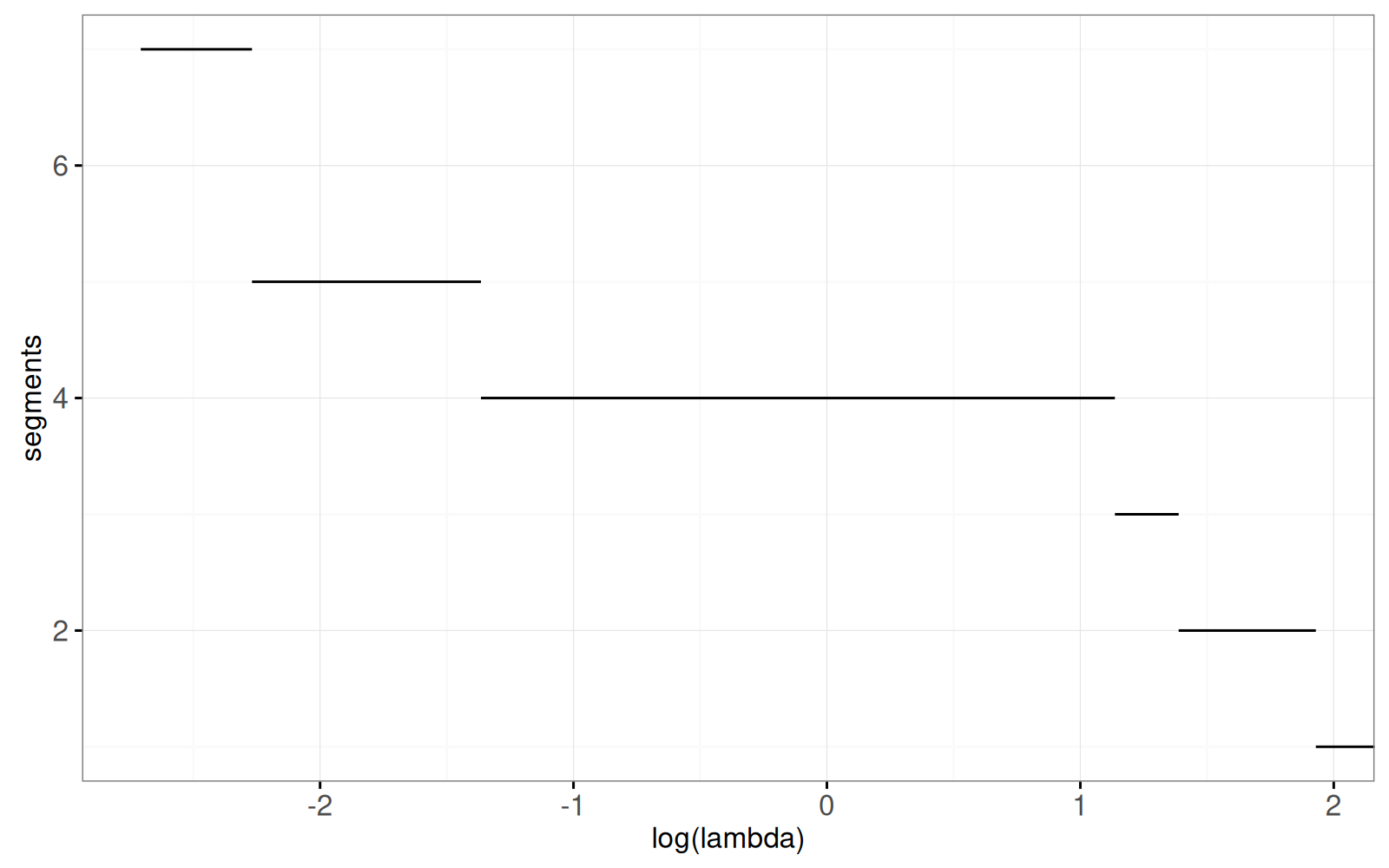
Dans le graphique ci-dessous, nous montrons la fonction de sélection du modèle $S^*(\lambda)$ pour ce jeu de données :
<!-- paragraph -->
```{r selection}
sig.selection <- data.table(
intreg$selection)[signal == sig.name & segments <= show.segs]
gg.selection <- ggplot()+
theme_bw()+
geom_segment(aes(
min.L, segments,
xend=max.L, yend=segments),
data=sig.selection)+
xlab("log(lambda)")
gg.selection
```
<!-- paragraph -->
Le graphique ci-dessus montre clairement que la fonction de sélection du modèle est décroissante.
<!-- comment -->
Dans la prochaine section, nous réalisons une version interactive de ces deux graphiques dans laquelle nous pouvons cliquer sur le graphique de sélection de modèle afin de sélectionner le modèle.
<!-- paragraph -->
## Figures interactives pour un signal {#interactive-one}
<!-- paragraph -->
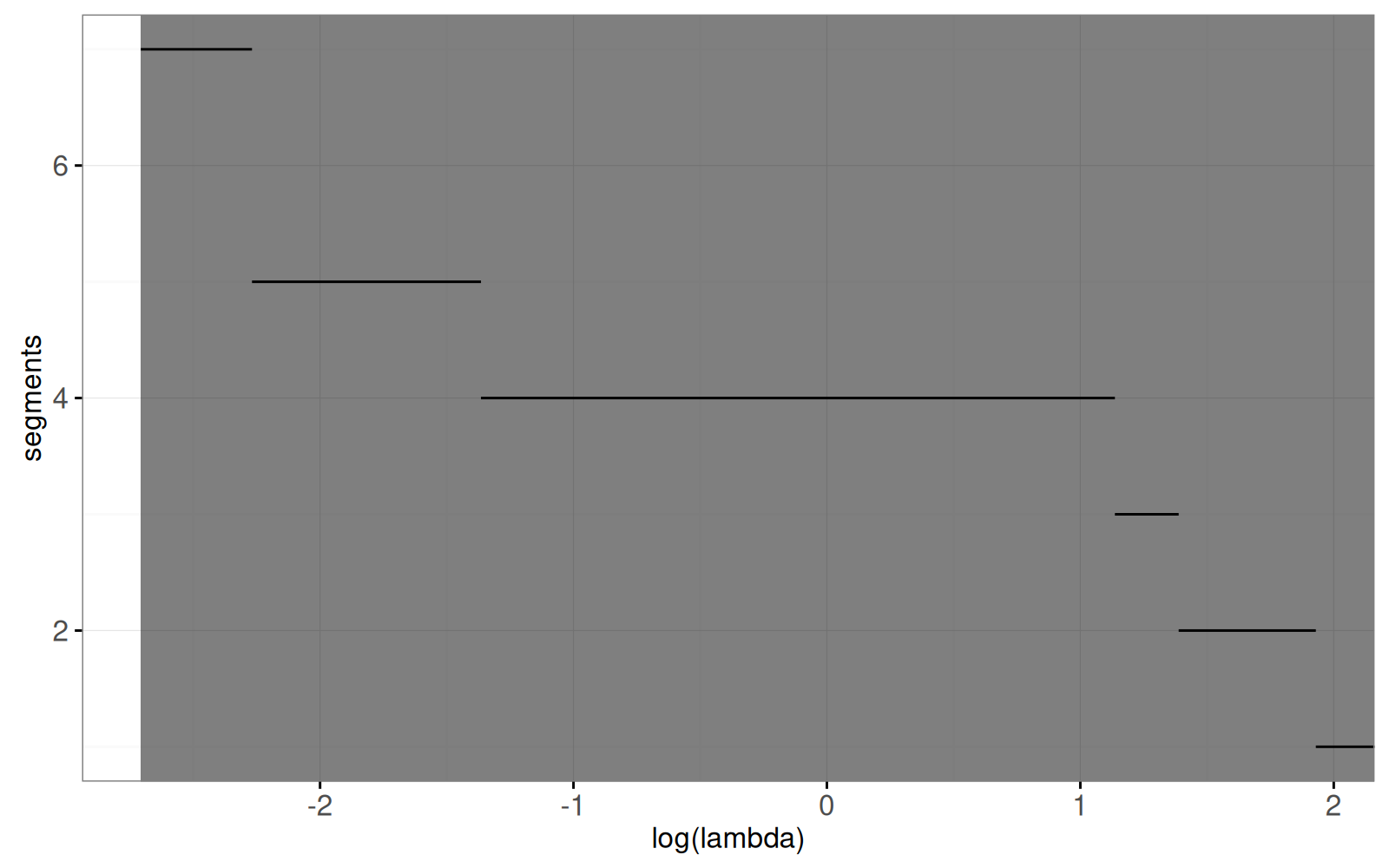
Nous allons créer une figure interactive pour un signal en ajoutant un `geom_tallrect()` avec `clickSelects=segments` au graphique ci-dessus :
<!-- paragraph -->
```{r selectionClick}
interactive.selection <- gg.selection+
geom_tallrect(aes(
xmin=min.L, xmax=max.L),
clickSelects="segments",
data=sig.selection,
color=NA,
fill="black",
alpha=0.5)
interactive.selection
```
<!-- paragraph -->
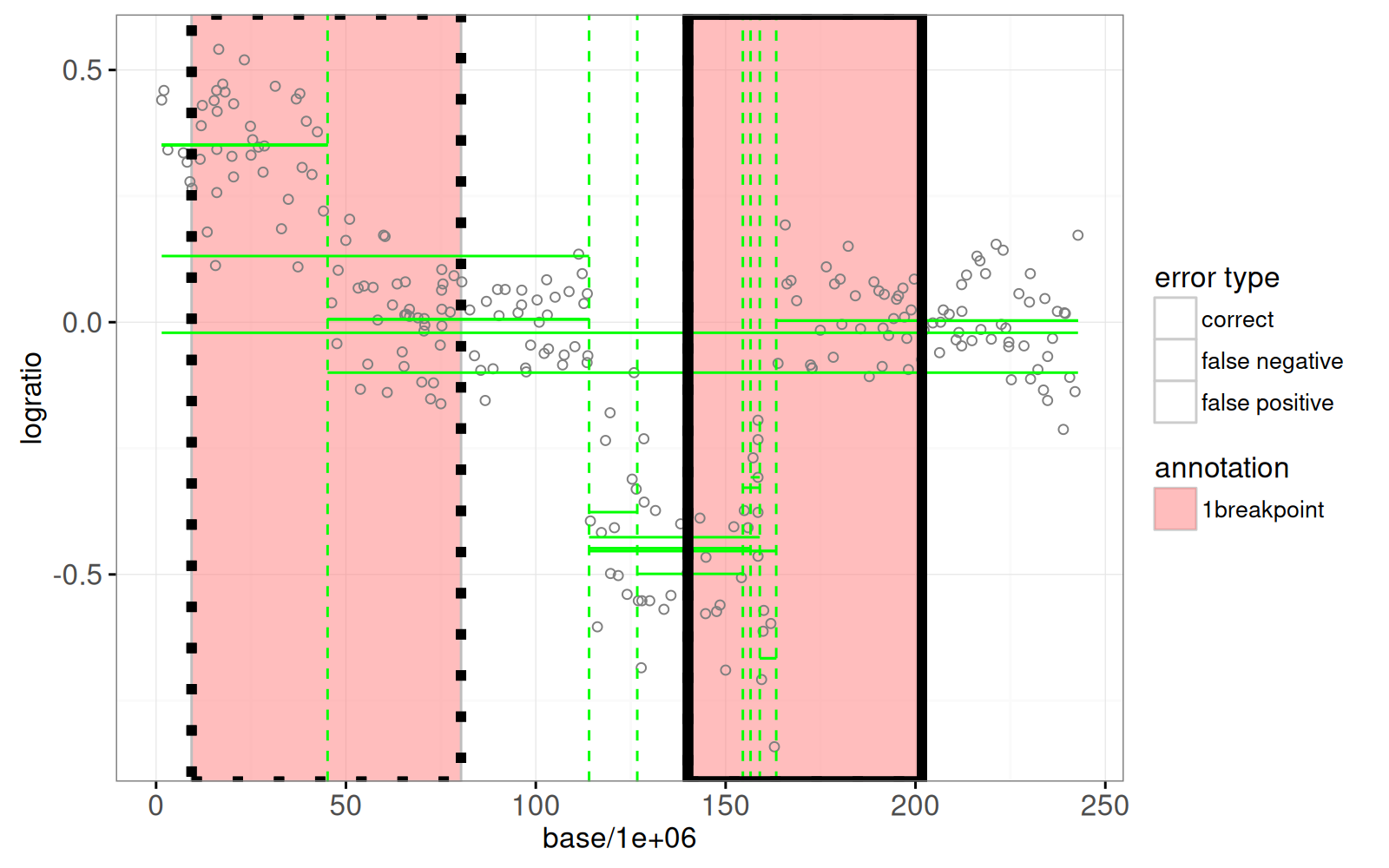
Nous allons combiner cela avec la version non facettée du graphique données/modèles ci-dessous, dans lequel nous avons ajouté `showSelected=segments` aux geoms des modèles :
<!-- paragraph -->
```{r selectionData}
interactive.models <- gg.one+
geom_segment(aes(
first.base/1e6, mean,
xend=last.base/1e6, yend=mean),
showSelected="segments",
color=model.color,
data=sig.segs)+
geom_vline(aes(
xintercept=base/1e6),
showSelected="segments",
color=model.color,
linetype="dashed",
data=sig.breaks)+
geom_tallrect(aes(
xmin=first.base/1e6, xmax=last.base/1e6,
linetype=status),
showSelected="segments",
data=sig.errors$label.errors,
size=2,
color="black",
fill=NA)+
scale_linetype_manual(
"type d'erreur",
values=c(
correct=0,
"false negative"=3,
"false positive"=1))
interactive.models
```
<!-- paragraph -->
Bien entendu, le graphique ci-dessus n’est pas très informatif car il n’est pas interactif.
<!-- comment -->
Ci-dessous, nous combinons les deux ggplots interactifs dans un `animint` :
<!-- paragraph -->
```{r interactiveOne}
animint(
models=interactive.models+
ggtitle("Modèle sélectionné"),
selection=interactive.selection+
ggtitle("Cliquer pour choisir le nombre de segments"))
```
<!-- paragraph -->
Notez que dans la visualisation des données ci-dessus, le modèle à 6 segments ne peut être sélectionné pour aucune valeur de lambda. Il n’est donc pas possible de cliquer sur le graphique pour sélectionner ce modèle.
<!-- comment -->
Cependant, il est possible de sélectionner le modèle en utilisant le menu de sélection des segments (cliquez sur « Show selection menus » au bas de la visualisation des données).
<!-- paragraph -->
## Graphique de régression de la marge maximale statique {#max-margin}
<!-- paragraph -->
Une autre partie de ce jeu de données est `intreg$intervals` qui comporte une ligne pour chaque signal.
<!-- comment -->
Les colonnes `min.L` et `max.L` indiquent les valeurs min/max de l’intervalle cible, qui correspond à la plage la plus large de valeurs de log(pénalité) avec des erreurs d’étiquette minimales.
<!-- comment -->
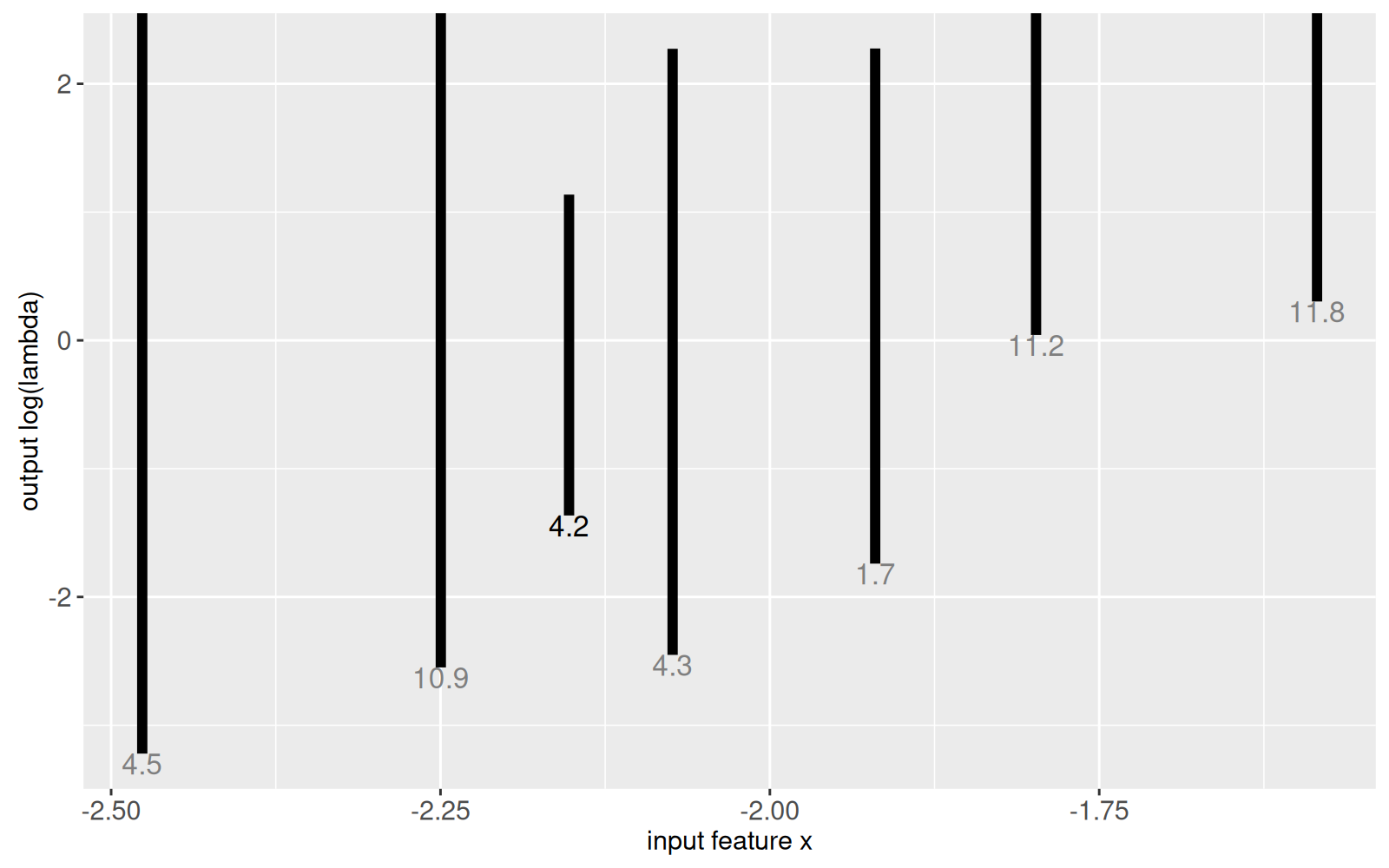
Nous traçons ci-dessous cet intervalle en fonction du logarithme du nombre de données dans la séquence :
<!-- paragraph -->
```{r intervals}
gg.intervals <- ggplot()+
geom_segment(aes(
feature, min.L,
xend=feature, yend=max.L),
size=2,
data=intreg$intervals)+
geom_text(aes(
feature, min.L, label=signal,
color=ifelse(signal==sig.name, "black", "grey50")),
vjust=1,
data=intreg$intervals)+
scale_color_identity()+
ylab("sortie de log(lambda)")+
xlab("variable d’entrée x")
gg.intervals
```
<!-- paragraph -->
Les intervalles cibles dans le graphique ci-dessus indiquent la région de l’espace log(lambda) qui sélectionnera un modèle avec des erreurs d’étiquette minimales.
<!-- comment -->
Il y a un intervalle pour chaque signal ; nous avons fait un `animint` dans la section précédente pour le signal indiqué dans le texte en noir.
<!-- comment -->
Des algorithmes d’apprentissage automatique peuvent être utilisés pour trouver une fonction de pénalité qui coupe chacun des intervalles et maximise la marge (la distance entre la fonction de régression et la limite de l’intervalle le plus proche).
<!-- comment -->
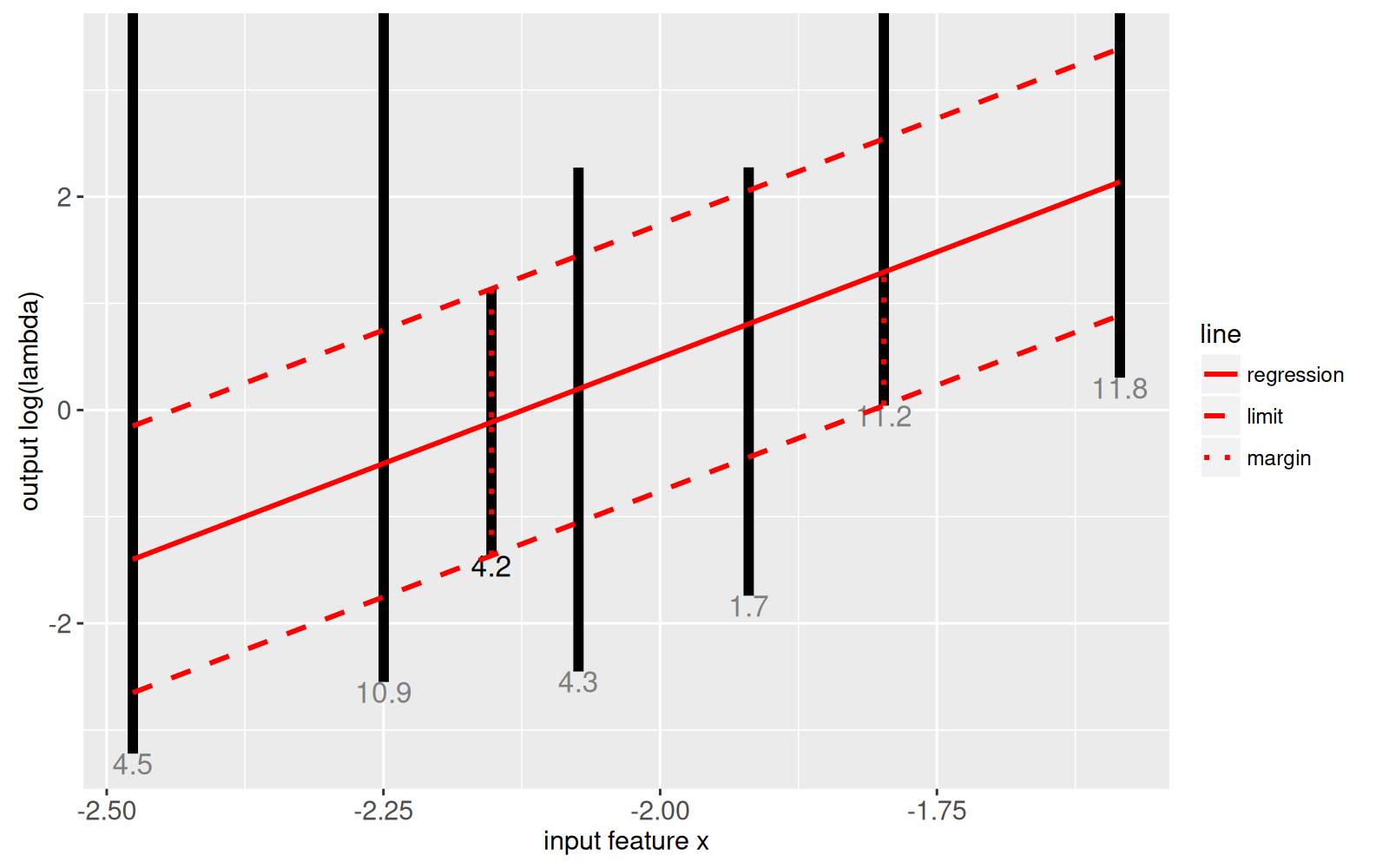
Les données pour la fonction de régression linéaire de la marge maximale sont dans `intreg$model` ce qui est illustré dans le graphique ci-dessous :
<!-- paragraph -->
```{r maxMargin}
gg.mm <- gg.intervals+
geom_segment(aes(
min.feature, min.L,
xend=max.feature, yend=max.L,
linetype=line),
color="red",
size=1,
data=intreg$model)+
scale_linetype_manual(
values=c(
regression="solid",
margin="dotted",
limit="dashed"))
gg.mm
```
<!-- paragraph -->
Le graphique ci-dessus montre la fonction de régression linéaire de la marge maximale f(x) sous la forme d’une ligne rouge pleine.
<!-- comment -->
Il est clair qu’elle coupe chacun des intervalles cibles noirs et maximise la marge (lignes pointillées verticales rouges).
<!-- comment -->
Pour plus d'informations sur le thème de la détection supervisée des points de rupture, voir [mon tutoriel useR 2017](https://github.com/tdhock/change-tutorial).
<!-- paragraph -->
Maintenant que vous savez comment visualiser chacune des sept parties du jeu de données `intreg`, le reste du chapitre est consacré à des exercices.
<!-- paragraph -->
## Résumé du chapitre et exercices {#ch16-exercises}
<!-- paragraph -->
Exercices :
<!-- paragraph -->
- Ajouter un `geom_text()` qui affiche le nom du signal actuellement sélectionné en haut du graphique, en `interactive.models` dans le premier `animint` ci-dessus.
<!-- comment -->
- Créez une animation avec deux graphiques qui montre l’ensemble de données correspondant à chaque intervalle sur le graphique de régression de la marge maximale.
<!-- comment -->
L’un des graphiques doit montrer une version interactive du graphique de régression de la marge maximale où vous pouvez cliquer sur un intervalle pour sélectionner un signal.
<!-- comment -->
L’autre graphique doit afficher le jeu de données pour le signal sélectionné.
<!-- comment -->
- Dans l’`animint` que vous avez créé dans l’exercice précédent, ajoutez un troisième graphique avec la fonction de sélection de modèle pour le signal actuellement sélectionné.
<!-- comment -->
- Dans la visualisation précédente, enlever le troisième graphique, et ajoutez une facette avec les mêmes informations au graphique de régression, avec les axes alignés.
<!-- comment -->
Ajoutez une autre facette qui indique le nombre d’étiquettes incorrectes (`intreg$selection$cost`) pour chaque valeur de log(lambda).
<!-- comment -->
- Ajoutez des geoms pour sélectionner le nombre de segments.
<!-- comment -->
En cliquant sur le graphique de sélection du modèle, on devrait sélectionner le nombre de segments, ce qui devrait mettre à jour le modèle affiché et les erreurs d’étiquette sur le graphique des données pour le signal actuellement sélectionné.
<!-- comment -->
En outre, ajoutez une indication visuelle du modèle sélectionné sur le graphique de régression de la marge maximale.
<!-- comment -->
Le résultat devrait ressembler à quelque chose [comme ceci](https://rcdata.nau.edu/genomic-ml/animint-gallery/2016-01-28-Max-margin-interval-regression-for-supervised-segmentation-model-selection/index.html).
<!-- comment -->
- Créez une autre visualisation des données en repartant du graphique à facettes `gg.signals` présenté au début de ce chapitre.
<!-- comment -->
Ajoutez un graphique permettant de sélectionner le nombre de segments pour chaque signal.
<!-- comment -->
Pour chaque signal dans le graphique à facettes des données, montrez le modèle actuellement sélectionné pour ce signal (il devrait y avoir une variable de sélection distincte pour chaque signal -- vous pouvez utiliser les `clickSelects` et `showSelected` nommés comme expliqué dans le [chapitre 14](/ch14)).
<!-- comment -->
Le résultat devrait ressembler à quelque chose [comme ceci](https://rcdata.nau.edu/genomic-ml/animint-gallery/2016-11-10-Max-margin-supervised-penalty-learning-for-peak-detection-in-ChIP-seq-data/index.html).
<!-- paragraph -->
Dans le [chapitre 17](/ch17), nous vous expliquerons comment visualiser l’algorithme d’agrégation des K-moyennes.
<!-- paragraph -->