# K plus proches voisins
```{r setup, echo=FALSE}
knitr::opts_chunk$set(fig.path="ch10-figures/")
```
<!-- paragraph -->
Dans ce chapitre, nous explorons plusieurs visualisations des données du classificateur des K plus proches voisins (KPPV).
<!-- paragraph -->
Plan du chapitre :
<!-- paragraph -->
- Nous commençons par la visualisation statique originale, repensée sous forme de deux ggplots affichés par `animint2` : un graphique de l’erreur de validation à 10 divisions et un graphique des prédictions du classificateur des 7 plus proches voisins.
<!-- comment -->
<!-- comment -->
- Nous proposons une refonte permettant de sélectionner le nombre de voisins utilisés pour les prédictions du modèle.
<!-- comment -->
- Nous proposons une seconde refonte permettant de sélectionner le nombre de plis utilisés pour le calcul de l’erreur de validation croisée.
<!-- paragraph -->
## Figure statique originale {#knn-static}
<!-- paragraph -->
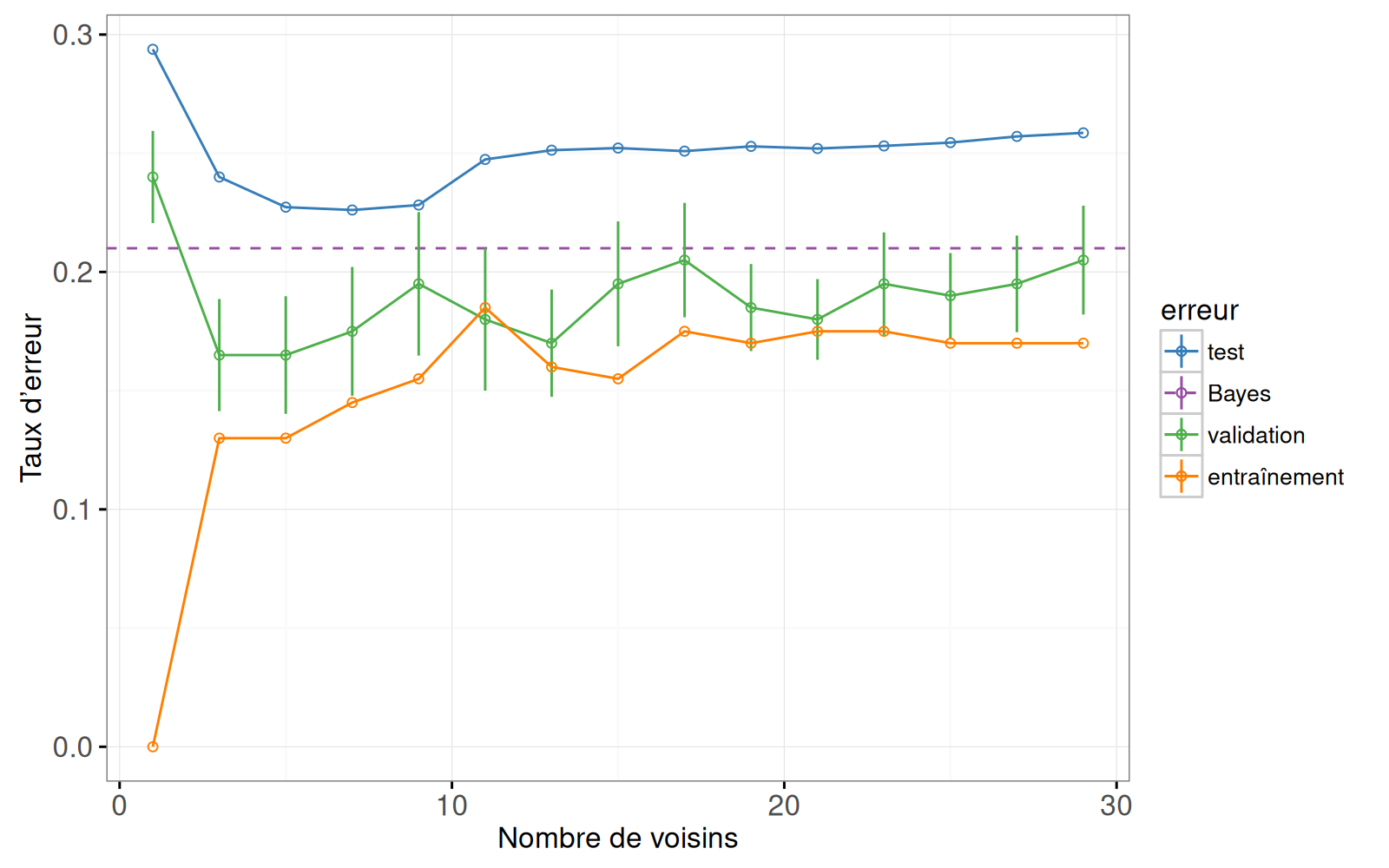
Notre objectif, dans ce chapitre, est de produire une version interactive de la figure 13.4 tirée de [*Elements of Statistical Learning*](http://statweb.stanford.edu/~tibs/ElemStatLearn/) [@Hastie2009].
<!-- comment -->
Cette figure se compose de deux graphiques :
<!-- paragraph -->
<!-- paragraph -->
À gauche : les courbes d’erreur de mauvaise classification, en fonction du nombre de voisins.
<!-- paragraph -->
- `geom_line()` et `geom_point()` pour les courbes d’erreur.
<!-- comment -->
- `geom_linerange()` pour les barres d’erreur de la courbe d’erreur de validation.
<!-- comment -->
- `geom_hline()` pour l’erreur de Bayes.
<!-- comment -->
- x = voisins.
<!-- comment -->
- y = pourcentage d’erreur.
<!-- comment -->
- couleur = type d’erreur.
<!-- paragraph -->
À droite : les données et les limites de décision dans l’espace bidimensionnel des variables d’entrée.
<!-- paragraph -->
- `geom_point()` pour les points de données.
<!-- comment -->
- `geom_point()` pour les prédictions de classification sur la grille en arrière-plan.
<!-- comment -->
- `geom_path()` pour les limites de décision.
<!-- comment -->
- `geom_text()` pour les taux d’erreur (entraînement, test et Bayes).
<!-- paragraph -->
### Graphique des courbes d’erreurs de classification {#static-error}
<!-- paragraph -->
Nous commençons par charger l’ensemble des données.
<!-- paragraph -->
```{r}
if(!requireNamespace("animint2data"))
remotes::install_github("animint/animint2data")
data(ESL.mixture, package="animint2data")
str(ESL.mixture)
```
<!-- paragraph -->
Nous utiliserons les éléments suivants de cet ensemble de données :
<!-- paragraph -->
- `x` : la matrice des variables d’entrée de l’ensemble de données d’apprentissage (200 observations sur les lignes x 2 variables numériques sur les colonnes).
<!-- comment -->
- `y` : le vecteur de sortie de l’ensemble de données d’apprentissage (200 étiquettes de classe, soit 0 ou 1).
<!-- comment -->
- `xnew` : la matrice représentant la grille de points dans l’espace des variables d’entrée, où seront affichées les prédictions de la fonction de classification (6831 points de la grille sur les lignes x 2 variables numériques sur les colonnes).
<!-- comment -->
- `prob` : la probabilité de la classe 1 à chacun des points de la grille (6831 valeurs numériques comprises entre 0 et 1).
<!-- comment -->
- `px1` : la grille de points pour le premier variable d’entrée (69 valeurs numériques comprises entre -2,6 et 4,2).
<!-- comment -->
Ces points seront utilisés pour calculer la limite de décision de Bayes à l’aide de la fonction `contourLines`.
<!-- comment -->
- `px2` : la grille de points pour la deuxième variable d’entrée (99 valeurs numériques comprises entre -2 et 2,9).
<!-- comment -->
- `means` : les 20 centres des distributions normales dans le modèle de simulation (20 centres sur les lignes x 2 variables sur les colonnes).
<!-- paragraph -->
Tout d’abord, nous créons un ensemble de test, en suivant le code d’exemple de `help(ESL.mixture)`.
<!-- comment -->
Notez que nous utilisons un `data.table` plutôt qu’un `data.frame` pour stocker ces données volumineuses, puisque `data.table` est souvent plus rapide et plus économe en mémoire pour les ensembles de données volumineux.
<!-- paragraph -->
```{r}
library(MASS)
library(data.table)
set.seed(123)
centers <- c(
sample(1:10, 5000, replace=TRUE),
sample(11:20, 5000, replace=TRUE))
mix.test <- mvrnorm(10000, c(0,0), 0.2*diag(2))
test.points <- data.table(
mix.test + ESL.mixture$means[centers,],
label=factor(c(rep(0, 5000), rep(1, 5000))))
test.points
```
<!-- paragraph -->
Nous créons ensuite un tableau de données qui comprend tous les points de test et les points de la grille, que nous utiliserons dans l’argument test de la fonction KPPV.
<!-- paragraph -->
```{r}
pred.grid <- data.table(ESL.mixture$xnew, label=NA)
input.cols <- c("V1", "V2")
names(pred.grid)[1:2] <- input.cols
test.and.grid <- rbind(
data.table(test.points, set="test"),
data.table(pred.grid, set="grid"))
test.and.grid$fold <- NA
test.and.grid
```
<!-- paragraph -->
Nous assignons aléatoirement chaque observation de l’ensemble de données d’apprentissage à l’un des 10 divisions.
<!-- paragraph -->
```{r}
n.folds <- 10
set.seed(2)
mixture <- with(ESL.mixture, data.table(x, label=factor(y)))
mixture$fold <- sample(rep(1:n.folds, l=nrow(mixture)))
mixture
```
<!-- paragraph -->
Nous définissons la fonction `OneFold` pour diviser les 200 observations en un ensemble d’entraînement et un ensemble de validation.
<!-- comment -->
Elle calcule ensuite la probabilité prédite par le classificateur des K plus proches voisins pour chacun des points de données dans tous les ensembles (entraînement, validation, test et grille).
<!-- paragraph -->
```{r}
OneFold <- function(validation.fold){
set <- ifelse(mixture$fold == validation.fold, "validation", "train")
fold.data <- rbind(test.and.grid, data.table(mixture, set))
fold.data$data.i <- 1:nrow(fold.data)
only.train <- subset(fold.data, set == "train")
data.by.neighbors <- list()
for(neighbors in seq(1, 30, by=2)){
if(interactive())cat(sprintf(
"n.folds=%4d validation.fold=%d neighbors=%d\n",
n.folds, validation.fold, neighbors))
set.seed(1)
pred.label <- class::knn( # random tie-breaking.
only.train[, input.cols, with=FALSE],
fold.data[, input.cols, with=FALSE],
only.train$label,
k=neighbors,
prob=TRUE)
prob.winning.class <- attr(pred.label, "prob")
fold.data$probability <- ifelse(
pred.label=="1", prob.winning.class, 1-prob.winning.class)
fold.data[, pred.label := ifelse(0.5 < probability, "1", "0")]
fold.data[, is.error := label != pred.label]
fold.data[, prediction := ifelse(is.error, "erronée", "correcte")]
data.by.neighbors[[paste(neighbors)]] <-
data.table(neighbors, fold.data)
}#for(neighbors
do.call(rbind, data.by.neighbors)
}#for(validation.fold
```
<!-- paragraph -->
Ci-dessous, nous exécutons la fonction `OneFold` en parallèle à l’aide du package `future`.
<!-- comment -->
Pour `validation.fold` de 1 à 10, on calcule l’erreur de l’ensemble de validation.
<!-- comment -->
Pour `validation.fold=0`, on traite l’ensemble des 200 observations comme un ensemble d’entraînement, qui sera utilisé pour visualiser les limites de décision apprises des K plus proches voisins.
<!-- paragraph -->
```{r}
future::plan("multisession")
data.all.folds.list <- future.apply::future_lapply(
0:n.folds, function(validation.fold){
one.fold <- OneFold(validation.fold)
data.table(validation.fold, one.fold)
}, future.seed = NULL)
(data.all.folds <- do.call(rbind, data.all.folds.list))
```
<!-- paragraph -->
Le tableau de données des prédictions contient près de 3 millions d’observations !
<!-- comment -->
Lorsqu’il y a autant de données, il n’est ni pratique ni informatif de les visualiser simultanément, nous allons donc calculer et tracer des statistiques sommaires.
<!-- comment -->
Dans le code ci-dessous, nous calculons la moyenne et l’erreur standard de l’erreur de mauvaise classification pour chaque modèle (sur les 10 divisions dans la validation croisée).
<!-- paragraph -->
```{r}
labeled.data <- data.all.folds[!is.na(label)]
error.stats <- labeled.data[, list(
error.prop=mean(is.error)
), by=.(set, validation.fold, neighbors)]
validation.error <- error.stats[set=="validation", list(
mean=mean(error.prop),
sd=sd(error.prop)/sqrt(.N)
), by=.(set, neighbors)]
validation.error
```
<!-- paragraph -->
Nous construisons ci-dessous des tableaux de données pour l’erreur d’entraînement et pour l’erreur de Bayes (nous savons qu’elle est de 0,21 pour les données de l’exemple de mélange).
<!-- paragraph -->
```{r}
Bayes.error <- data.table(
set="Bayes",
validation.fold=NA,
neighbors=NA,
error.prop=0.21)
Bayes.error
other.error <- error.stats[validation.fold==0]
head(other.error)
```
<!-- paragraph -->
Ci-dessous, nous construisons une palette de couleurs à partir de `dput(RColorBrewer::brewer.pal(Inf, "Set1"))` et des palettes de types de lignes (`linetype`).
<!-- paragraph -->
```{r}
set.colors <- c(
test="#377EB8", #blue
Bayes="#984EA3",#purple
validation="#4DAF4A",#green
entraînement="#FF7F00")#orange
classifier.linetypes <- c(
Bayes="dashed",
KPPV="solid")
set.linetypes <- set.colors
set.linetypes[] <- classifier.linetypes[["KPPV"]]
set.linetypes["Bayes"] <- classifier.linetypes[["Bayes"]]
cbind(set.linetypes, set.colors)
```
<!-- paragraph -->
Le code ci-dessous reproduit le graphique des courbes d’erreur de la figure originale.
<!-- paragraph -->
```{r}
library(animint2)
add_set_fr <- function(DT)DT[
, set_fr := ifelse(set=="train", "entraînement", set)]
add_set_fr(other.error)
add_set_fr(validation.error)
add_set_fr(Bayes.error)
legend.name.type <- "erreur"
errorPlotStatic <- ggplot()+
theme_bw()+
geom_hline(aes(
yintercept=error.prop, color=set_fr, linetype=set_fr),
data=Bayes.error)+
scale_color_manual(
legend.name.type,
values=set.colors,
breaks=names(set.colors))+
scale_linetype_manual(
legend.name.type,
values=set.linetypes,
breaks=names(set.linetypes))+
ylab("Taux d’erreur")+
xlab("Nombre de voisins")+
geom_linerange(aes(
neighbors, ymin=mean-sd, ymax=mean+sd,
color=set_fr),
data=validation.error)+
geom_line(aes(
neighbors, mean, linetype=set_fr, color=set_fr),
data=validation.error)+
geom_line(aes(
neighbors, error.prop,
group=set_fr, linetype=set_fr, color=set_fr),
data=other.error)+
geom_point(aes(
neighbors, mean, color=set_fr),
data=validation.error)+
geom_point(aes(
neighbors, error.prop, color=set_fr),
data=other.error)
errorPlotStatic
```
<!-- paragraph -->
### Graphique des limites de décision dans l’espace des variables d’entrée {#static-features}
<!-- paragraph -->
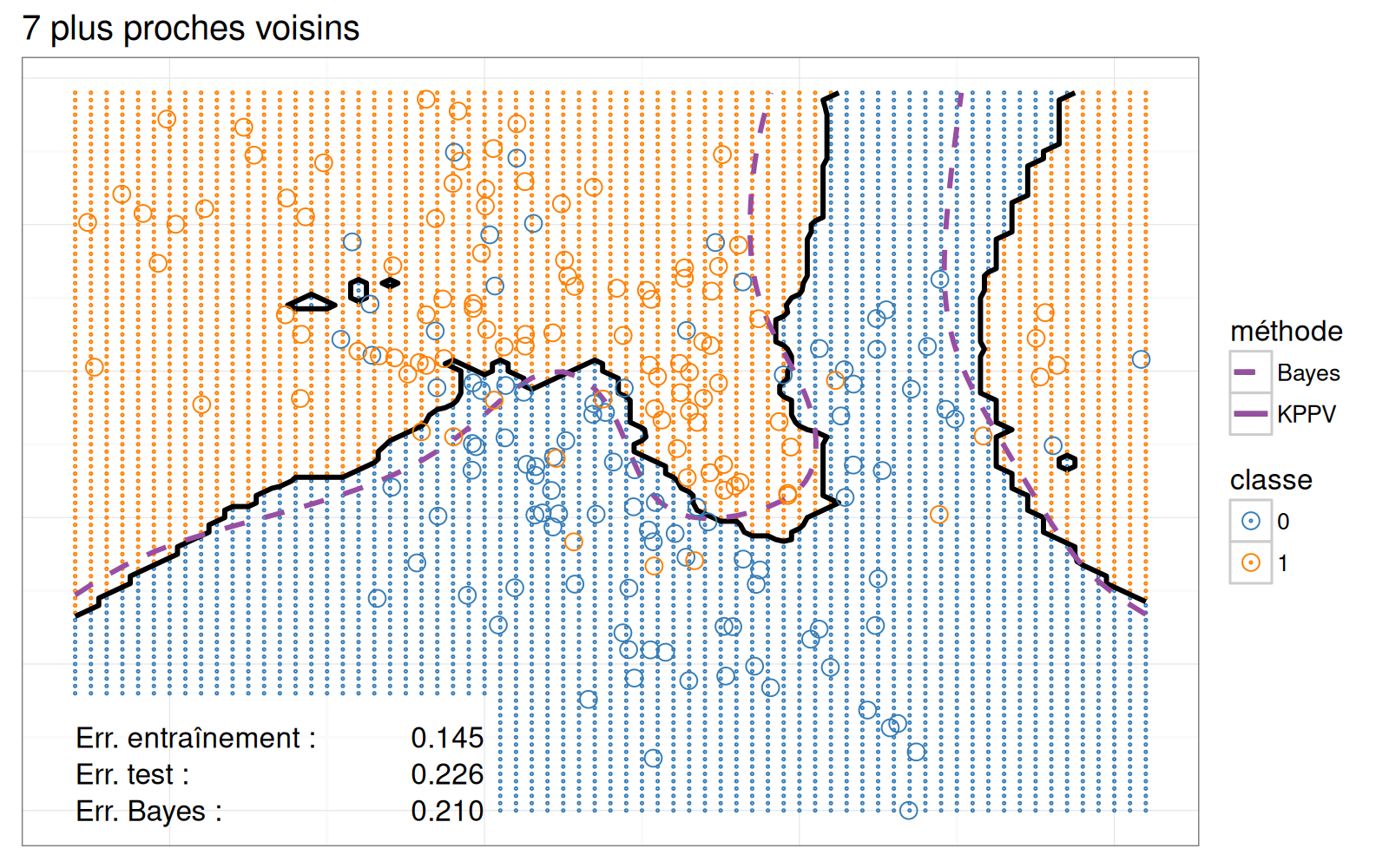
Pour la visualisation statique des données de l’espace des variables, nous ne montrons que le modèle avec 7 voisins.
<!-- paragraph -->
```{r}
show.neighbors <- 7
show.data <- data.all.folds[
validation.fold==0 & neighbors==show.neighbors]
show.points <- show.data[set=="train"]
show.points
```
<!-- paragraph -->
Ensuite, nous calculons les taux d’erreur de classification, que nous afficherons en bas à gauche du graphique de l’espace des variables.
<!-- paragraph -->
```{r}
text.height <- 0.25
text.V1.prop <- 0
text.V2.bottom <- -2
text.V1.error <- -2.6
error.text <- rbind(
Bayes.error,
other.error[neighbors==show.neighbors])
error.text[, V2.top := text.V2.bottom + text.height * (1:.N)]
error.text[, V2.bottom := V2.top - text.height]
error.text
```
<!-- paragraph -->
Nous définissons la fonction suivante, que nous utiliserons pour calculer les limites de décision.
<!-- paragraph -->
```{r}
getBoundaryDF <- function(prob.vec){
stopifnot(length(prob.vec) == 6831)
several.paths <- with(ESL.mixture, contourLines(
px1, px2,
matrix(prob.vec, length(px1), length(px2)),
levels=0.5))
contour.list <- list()
for(path.i in seq_along(several.paths)){
contour.list[[path.i]] <- with(several.paths[[path.i]], data.table(
path.i, V1=x, V2=y))
}
do.call(rbind, contour.list)
}
```
<!-- paragraph -->
Nous utilisons cette fonction pour calculer les limites de décision pour les 7 plus proches voisins et pour la fonction optimale de Bayes.
<!-- paragraph -->
```{r}
boundary.grid <- show.data[set=="grid"]
boundary.grid[, label := pred.label]
pred.boundary <- getBoundaryDF(boundary.grid$probability)
pred.boundary$classifier <- "KPPV"
Bayes.boundary <- getBoundaryDF(ESL.mixture$prob)
Bayes.boundary$classifier <- "Bayes"
Bayes.boundary
```
<!-- paragraph -->
Ci-dessous, nous ne considérons que les points de la grille qui ne chevauchent pas les étiquettes de texte.
<!-- paragraph -->
```{r}
on.text <- function(V1, V2){
V2 <= max(error.text$V2.top) & V1 <= text.V1.prop
}
(show.grid <- boundary.grid[!on.text(V1, V2)])
```
<!-- paragraph -->
Le nuage de points ci-dessous reproduit le classificateur des 7 plus proches voisins de la figure originale.
<!-- paragraph -->
```{r}
label.colors <- c(
"0"="#377EB8",
"1"="#FF7F00")
scatterPlotStatic <- ggplot()+
theme_bw()+
theme(axis.text=element_blank(),
axis.ticks=element_blank(),
axis.title=element_blank())+
ggtitle("7 plus proches voisins")+
scale_color_manual(
"classe",
values=label.colors)+
scale_linetype_manual(
"méthode",
values=classifier.linetypes)+
geom_point(aes(
V1, V2, color=label),
size=0.2,
data=show.grid)+
geom_path(aes(
V1, V2, group=path.i, linetype=classifier),
size=1,
data=pred.boundary)+
geom_path(aes(
V1, V2, group=path.i, linetype=classifier),
color=set.colors[["Bayes"]],
size=1,
data=Bayes.boundary)+
geom_point(aes(
V1, V2, color=label),
fill=NA,
size=3,
data=show.points)+
geom_text(aes(
text.V1.error, V2.bottom,
label=paste("Err.", set_fr, ":")),
data=error.text,
hjust=0)+
geom_text(aes(
text.V1.prop, V2.bottom, label=sprintf("%.3f", error.prop)),
data=error.text,
hjust=1)
scatterPlotStatic
```
<!-- paragraph -->
### Graphiques combinés {#static-combined}
<!-- paragraph -->
Enfin, nous combinons les deux `ggplots` et les affichons sous forme d’un `animint2`.
<!-- paragraph -->
```{r ch10-vis-static}
animint(
errorPlotStatic+
theme_animint(width=300),
scatterPlotStatic+
theme_animint(last_in_row=TRUE))
```
<!-- paragraph -->
Bien que cette visualisation comporte trois légendes interactives, elle est statique dans le sens où elle n’affiche que les prédictions du modèle des 7 plus proches voisins.
<!-- paragraph -->
## Sélectionner le nombre de voisins à l’aide de l’interactivité {#neighbors}
<!-- paragraph -->
Dans cette section, nous proposons une visualisation interactive qui permet à l’utilisateur de sélectionner K, le nombre de voisins.
### Graphique interactif des courbes d’erreur {#neighbors-error}
<!-- paragraph -->
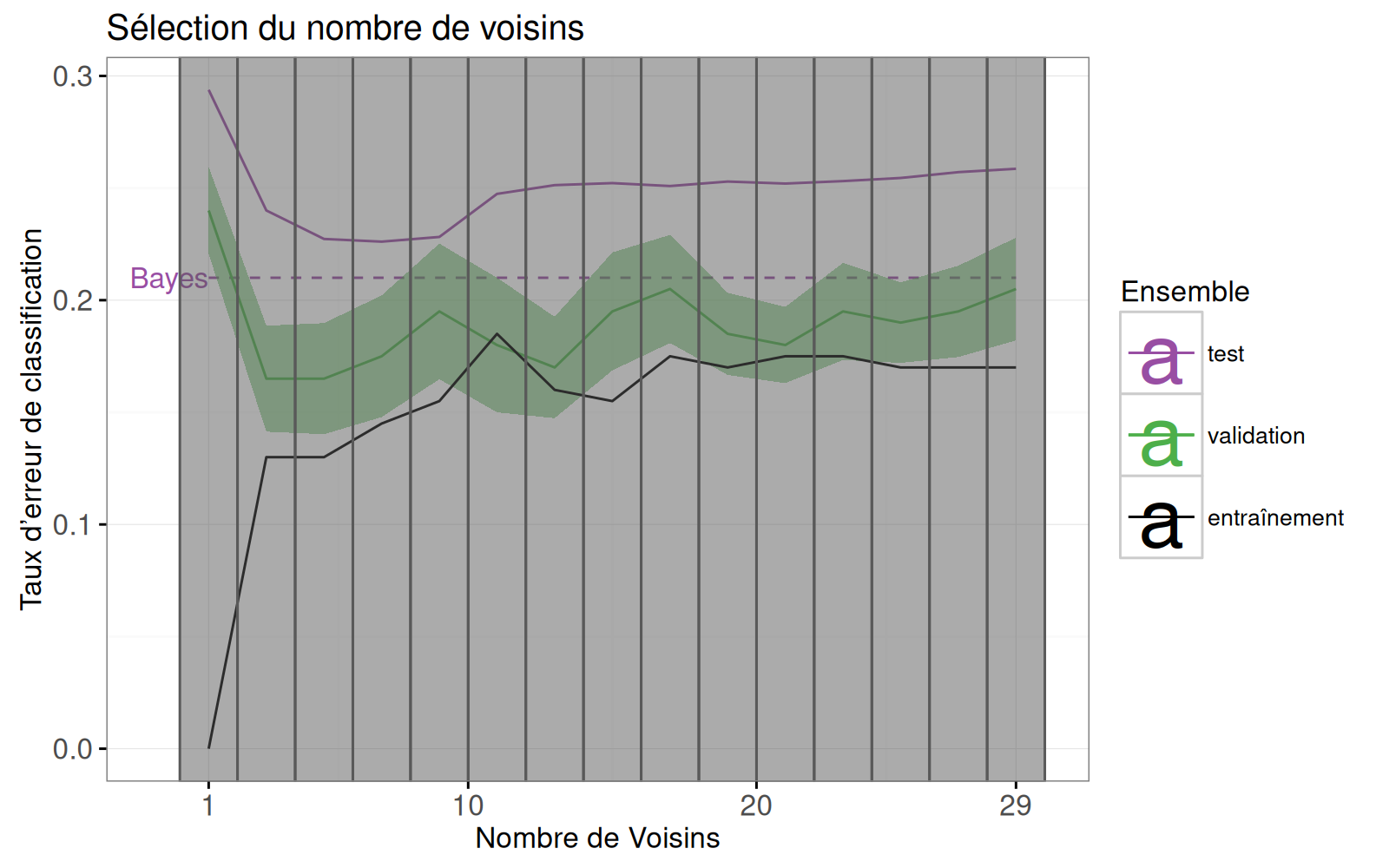
Examinons d’abord le graphique des courbes d’erreur.
<!-- paragraph -->
Nous voulons effectuer les modifications suivantes :
<!-- paragraph -->
- ajout d’un `geom_tallrect()` pour sélectionner le nombre de voisins ;
<!-- comment -->
- changement de la limite de décision de Bayes, passant d’un `geom_hline()` avec une entrée de légende, à un `geom_segment()` avec une étiquette de texte ;
<!-- comment -->
- ajout d’une légende de type de ligne pour distinguer les taux d’erreur des modèles de Bayes et de KPPV ;
<!-- comment -->
- remplacement des barres d’erreur, `geom_linerange()`, par des bandes d’erreur, `geom_ribbon()`.
<!-- paragraph -->
Les seules nouvelles données que nous devons définir sont les points d’extrémité du segment que nous utiliserons pour tracer la frontière de décision de Bayes.
<!-- comment -->
Notez que nous redéfinissons également l’ensemble test pour souligner que l’erreur de Bayes représente le meilleur taux d’erreur atteignable pour les données de test.
<!-- paragraph -->
```{r}
Bayes.segment <- data.table(
Bayes.error,
classifier="Bayes",
min.neighbors=1,
max.neighbors=29)
Bayes.segment$set_fr <- "test"
```
<!-- paragraph -->
Nous ajoutons également aux tableaux de données une variable d’erreur qui contient l’erreur de prédiction des modèles KPPV.
<!-- comment -->
Cette variable d’erreur sera utilisée pour la légende du type de ligne.
<!-- paragraph -->
```{r}
validation.error$classifier <- "KPPV"
other.error$classifier <- "KPPV"
```
<!-- paragraph -->
Nous redéfinissons le graphique des courbes d’erreur ci-dessous.
<!-- comment -->
Notez que :
<!-- paragraph -->
- Nous utilisons `showSelected` dans `geom_text()` et `geom_ribbon()` afin qu’ils soient masqués lorsque l’on clique sur les légendes interactives.
<!-- comment -->
- Nous utilisons `clickSelects` dans `geom_tallrect()` pour sélectionner le nombre de voisins.
<!-- comment -->
Les geoms cliquables doivent être placés en dernier (couche supérieure) afin de ne pas être masqués par les geoms non cliquables (couches inférieures).
<!-- paragraph -->
```{r}
set.colors <- c(
test="#984EA3",#purple
validation="#4DAF4A",#green
Bayes="#984EA3",#purple
entraînement="black")
legend.name <- "Ensemble"
errorPlot <- ggplot()+
ggtitle("Sélection du nombre de voisins")+
theme_bw()+
geom_text(aes(
min.neighbors, error.prop,
color=set_fr, label="Bayes"),
showSelected="classifier",
hjust=1,
data=Bayes.segment)+
geom_segment(aes(
min.neighbors, error.prop,
xend=max.neighbors, yend=error.prop,
color=set_fr,
linetype=classifier),
showSelected="classifier",
data=Bayes.segment)+
scale_color_manual(
legend.name,
values=set.colors, breaks=names(set.colors))+
scale_fill_manual(
legend.name,
values=set.colors)+
scale_linetype_manual(
legend.name,
values=classifier.linetypes)+
guides(fill="none", linetype="none")+
ylab("Taux d’erreur de classification")+
scale_x_continuous(
"Nombre de Voisins",
limits=c(-1, 30),
breaks=c(1, 10, 20, 29))+
geom_ribbon(aes(
neighbors, ymin=mean-sd, ymax=mean+sd,
fill=set_fr),
showSelected=c("classifier", "set_fr"),
alpha=0.5,
color="transparent",
data=validation.error)+
geom_line(aes(
neighbors, mean, color=set_fr,
linetype=classifier),
showSelected="classifier",
data=validation.error)+
geom_line(aes(
neighbors, error.prop, group=set_fr, color=set_fr,
linetype=classifier),
showSelected="classifier",
data=other.error)+
geom_tallrect(aes(
xmin=neighbors-1, xmax=neighbors+1),
clickSelects="neighbors",
alpha=0.5,
data=validation.error)
errorPlot
```
<!-- paragraph -->
### Graphique de l’espace des éléments montrant le nombre de voisins sélectionnés. {#neighbors-features}
<!-- paragraph -->
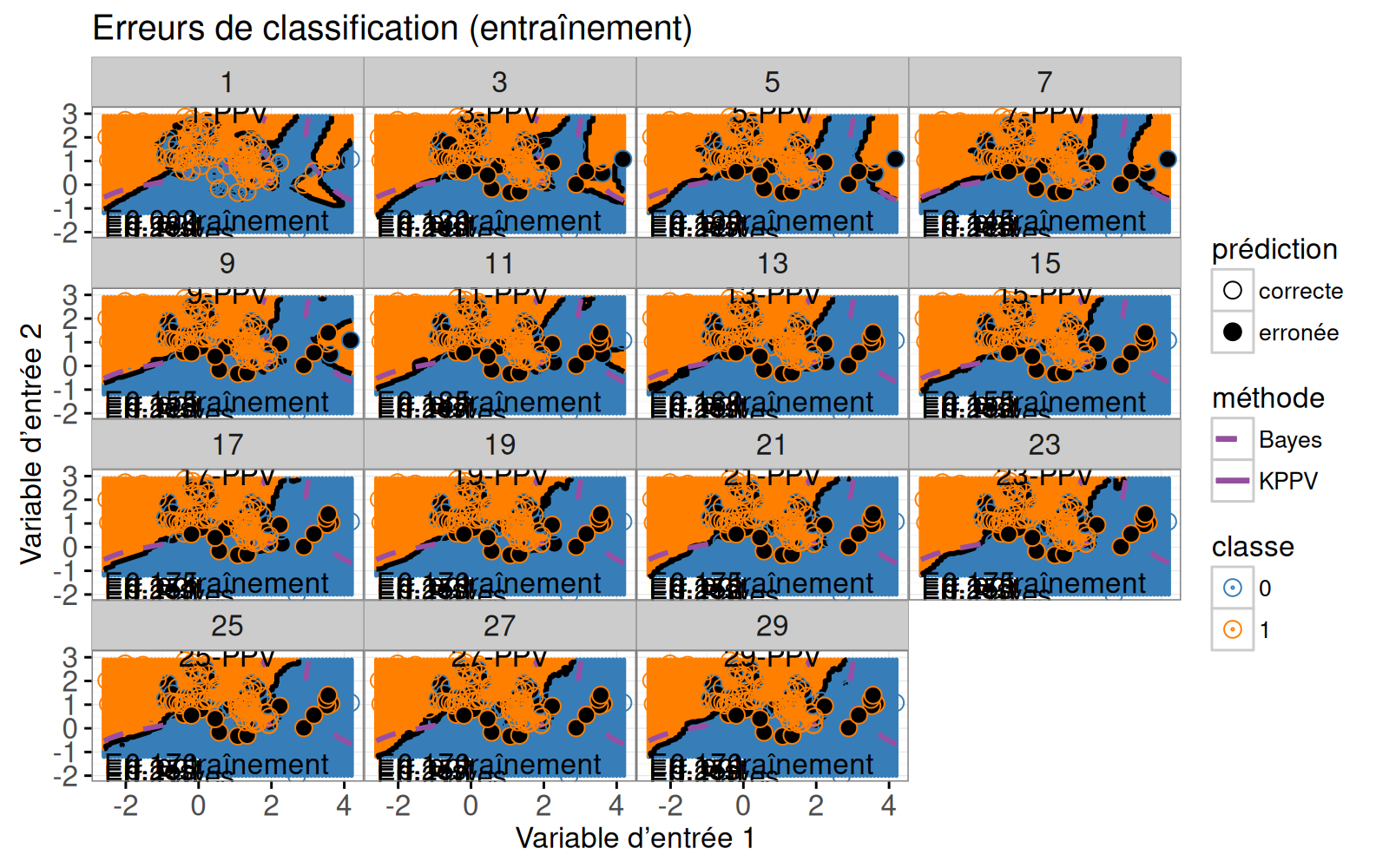
Concentrons-nous maintenant sur le graphique de l’espace des variables d’entrée.
<!-- comment -->
Dans la section précédente, nous n’avons considéré que le sous-ensemble de données du modèle à 7 voisins.
<!-- comment -->
Nous proposons les modifications suivantes :
<!-- paragraph -->
- Nous utilisons les voisins comme variable `showSelected`.
<!-- comment -->
- Nous ajoutons une légende pour indiquer les points de données d’entraînement mal classées.
<!-- comment -->
- Nous utilisons des coordonnées à espacement égal afin que la distance visuelle (pixels) soit la même que la distance euclidienne dans l’espace des variables.
<!-- paragraph -->
```{r}
show.data <- data.all.folds[validation.fold==0]
(show.points <- show.data[set=="train"])
```
<!-- paragraph -->
Ci-dessous, nous calculons les limites de décision prédites séparément pour chaque modèle de K plus proches voisins.
<!-- paragraph -->
```{r}
boundary.grid <- show.data[set=="grid"]
boundary.grid[, label := pred.label]
show.grid <- boundary.grid[!on.text(V1, V2)]
pred.boundary <- boundary.grid[
, getBoundaryDF(probability), by=neighbors]
pred.boundary$classifier <- "KPPV"
pred.boundary
```
<!-- paragraph -->
Au lieu d’afficher le nombre de voisins dans le titre du graphique, nous créons ci-dessous un élément `geom_text()` qui sera mis à jour en fonction du nombre de voisins sélectionnés.
<!-- paragraph -->
```{r}
show.text <- show.grid[, list(
V1=mean(range(V1)), V2=3.05), by=neighbors]
```
<!-- paragraph -->
Nous calculons ci-dessous la position du texte qui affichera, en bas à gauche, le taux d’erreur du modèle sélectionné.
<!-- paragraph -->
```{r}
other.error[, V2.bottom := rep(
text.V2.bottom + text.height * 1:2, l=.N)]
```
<!-- paragraph -->
Ci-dessous, nous redéfinissons les données de l’erreur de Bayes sans colonne de voisins, afin qu’elles apparaissent dans chaque sous-ensemble `showSelected`.
<!-- paragraph -->
```{r}
Bayes.error <- data.table(
set_fr="Bayes",
error.prop=0.21)
```
<!-- paragraph -->
Enfin, nous redéfinissons le graphique, en utilisant le nombre de voisins (`neighbors`) comme variable `showSelected` dans plusieurs geoms.
<!-- paragraph -->
```{r}
err_set <- function(set)paste("Err.", set)
scatterPlot <- ggplot()+
ggtitle("Erreurs de classification (entraînement)")+
theme_bw()+
xlab("Variable d’entrée 1")+
ylab("Variable d’entrée 2")+
scale_linetype_manual(
"méthode", values=classifier.linetypes)+
scale_fill_manual(
"prédiction",
values=c(erronée="black", correcte="transparent"))+
scale_color_manual("classe", values=label.colors)+
geom_point(aes(
V1, V2, color=label),
showSelected="neighbors",
size=0.2,
data=show.grid)+
geom_path(aes(
V1, V2, group=path.i, linetype=classifier),
showSelected="neighbors",
size=1,
data=pred.boundary)+
geom_path(aes(
V1, V2, group=path.i, linetype=classifier),
color=set.colors[["test"]],
size=1,
data=Bayes.boundary)+
geom_point(aes(
V1, V2, color=label,
fill=prediction),
showSelected="neighbors",
size=3,
data=show.points)+
geom_text(aes(
text.V1.error, text.V2.bottom, label=err_set(set_fr)),
data=Bayes.error,
hjust=0)+
geom_text(aes(
text.V1.prop, text.V2.bottom, label=sprintf("%.3f", error.prop)),
data=Bayes.error,
hjust=1)+
geom_text(aes(
text.V1.error, V2.bottom, label=err_set(set_fr)),
showSelected="neighbors",
data=other.error,
hjust=0)+
geom_text(aes(
text.V1.prop, V2.bottom, label=sprintf("%.3f", error.prop)),
showSelected="neighbors",
data=other.error,
hjust=1)+
geom_text(aes(
V1, V2,
label=paste0(neighbors, "-PPV")),
showSelected="neighbors",
data=show.text)
```
<!-- paragraph -->
Avant de compiler la visualisation des données interactive, nous imprimons un `ggplot` statique avec une facette pour chaque valeur de voisins.
<!-- paragraph -->
```{r}
scatterPlot+
facet_wrap("neighbors")+
theme(panel.margin=grid::unit(0, "lines"))
```
<!-- paragraph -->
### Visualisation des données interactive combinée {#neighbors-combined}
<!-- paragraph -->
Enfin, nous combinons les deux graphiques dans une visualisation unique avec le nombre de voisins (`neighbors`) comme variable de sélection.
<!-- paragraph -->
```{r ch10-vis-neighbors}
animint(
errorPlot+
theme_animint(width=300),
scatterPlot+
theme_animint(width=450, last_in_row=TRUE),
first=list(neighbors=7),
time=list(variable="neighbors", ms=3000))
```
<!-- paragraph -->
Notez que le nombre de voisins (`neighbors`) est utilisé comme variable de temps, de sorte que l’animation montre les prédictions des différents modèles.
<!-- paragraph -->
## Sélectionner le nombre de divisions dans la validation croisée {#folds}
<!-- paragraph -->
Dans cette section, nous proposons une visualisation qui permet à l’utilisateur de sélectionner le nombre de divisions utilisées pour calculer la courbe d’erreur de validation.
<!-- paragraph -->
La boucle `for` ci-dessous calcule la courbe d’erreur de validation pour différentes valeurs de `n.folds`.
<!-- paragraph -->
```{r}
error.by.folds <- list()
error.by.folds[["10"]] <- data.table(n.folds=10, validation.error)
for(n.folds in c(3, 5, 15)){
set.seed(2)
mixture <- with(ESL.mixture, data.table(x, label=factor(y)))
mixture$fold <- sample(rep(1:n.folds, l=nrow(mixture)))
only.validation.list <- future.apply::future_lapply(
1:n.folds, function(validation.fold){
one.fold <- OneFold(validation.fold)
data.table(validation.fold, one.fold[set=="validation"])
}, future.seed=NULL)
only.validation <- do.call(rbind, only.validation.list)
only.validation.error <- only.validation[, list(
error.prop=mean(is.error)
), by=.(set, set_fr=set, validation.fold, neighbors)]
only.validation.stats <- only.validation.error[, list(
mean=mean(error.prop),
sd=sd(error.prop)/sqrt(.N)
), by=.(set, set_fr=set, neighbors)]
error.by.folds[[paste(n.folds)]] <-
data.table(n.folds, only.validation.stats, classifier="KPPV")
}
validation.error.several <- do.call(rbind, error.by.folds)
```
<!-- paragraph -->
Le code ci-dessous calcule le minimum de la courbe d’erreur pour chaque valeur de `n.folds`.
<!-- paragraph -->
```{r}
min.validation <- validation.error.several[
, .SD[which.min(mean)], by=n.folds]
```
<!-- paragraph -->
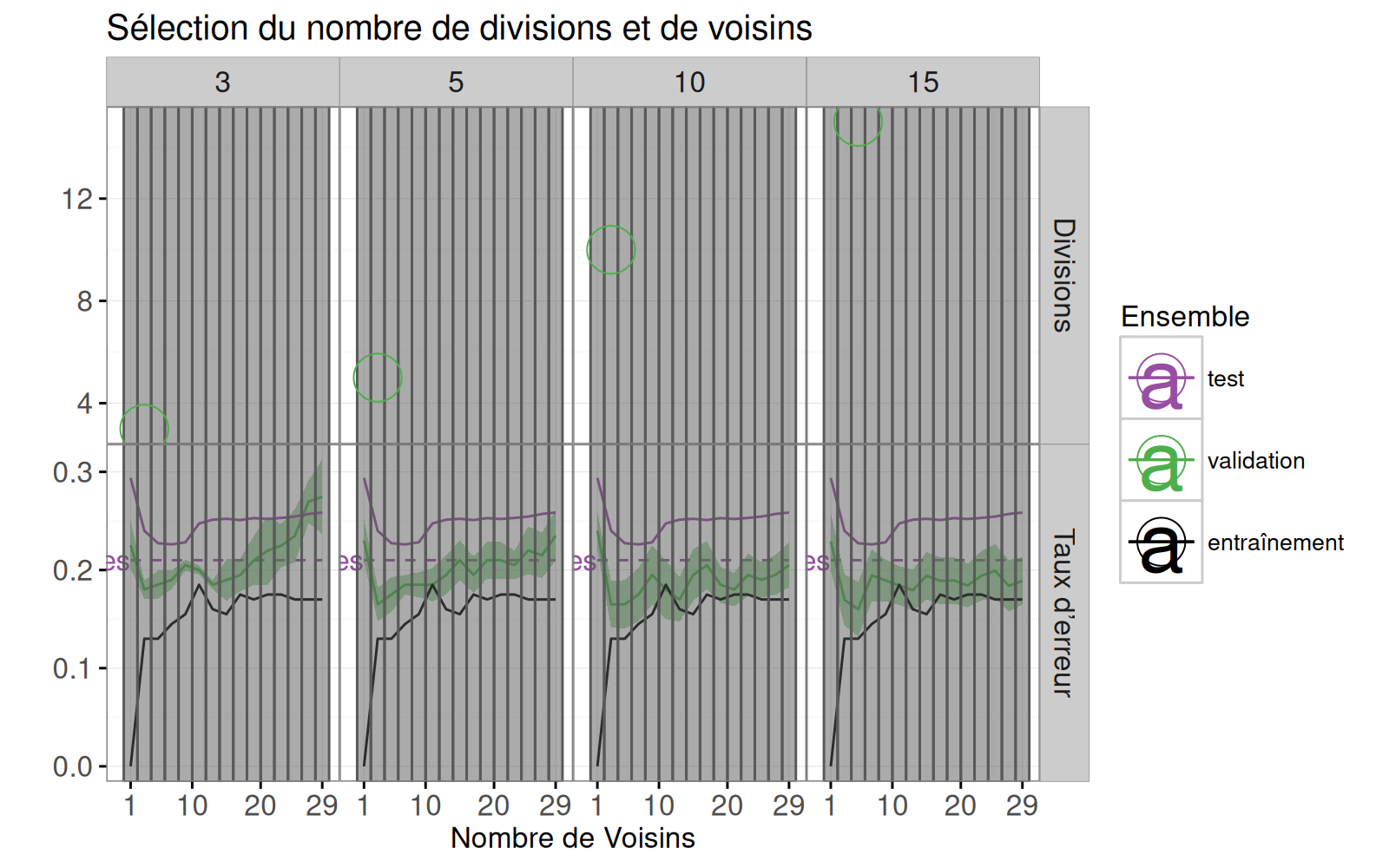
Le code ci-dessous crée un nouveau graphique de courbe d’erreur à deux facettes.
<!-- paragraph -->
```{r}
facets <- function(df, facet){
data.frame(df, facet=factor(facet, c("Divisions", "Taux d’erreur")))
}
errorPlotNew <- ggplot()+
ggtitle("Sélection du nombre de divisions et de voisins")+
theme_bw()+
theme(panel.margin=grid::unit(0, "cm"))+
facet_grid(facet ~ ., scales="free")+
geom_text(aes(
min.neighbors, error.prop,
color=set_fr, label="Bayes"),
showSelected="classifier",
hjust=1,
data=facets(Bayes.segment, "Taux d’erreur"))+
geom_segment(aes(
min.neighbors, error.prop,
xend=max.neighbors, yend=error.prop,
color=set_fr,
linetype=classifier),
showSelected="classifier",
data=facets(Bayes.segment, "Taux d’erreur"))+
scale_color_manual(
legend.name, values=set.colors, breaks=names(set.colors))+
scale_fill_manual(
legend.name, values=set.colors, breaks=names(set.colors))+
scale_linetype_manual(
legend.name, values=classifier.linetypes)+
guides(fill="none", linetype="none")+
ylab("")+
scale_x_continuous(
"Nombre de Voisins",
limits=c(-1, 30),
breaks=c(1, 10, 20, 29))+
geom_ribbon(aes(
neighbors, ymin=mean-sd, ymax=mean+sd,
fill=set_fr),
showSelected=c("classifier", "set_fr", "n.folds"),
alpha=0.5,
color="transparent",
data=facets(validation.error.several, "Taux d’erreur"))+
geom_line(aes(
neighbors, mean, color=set_fr,
linetype=classifier),
showSelected=c("classifier", "n.folds"),
data=facets(validation.error.several, "Taux d’erreur"))+
geom_line(aes(
neighbors, error.prop, group=set_fr, color=set_fr,
linetype=classifier),
showSelected="classifier",
data=facets(other.error, "Taux d’erreur"))+
geom_tallrect(aes(
xmin=neighbors-1, xmax=neighbors+1),
clickSelects="neighbors",
alpha=0.5,
data=validation.error)+
geom_point(aes(
neighbors, n.folds, color=set_fr),
clickSelects="n.folds",
size=9,
data=facets(min.validation, "Divisions"))
```
<!-- paragraph -->
Le code ci-dessous prévisualise le nouveau graphique de la courbe d’erreur, en ajoutant une facette supplémentaire pour la variable `showSelected`.
<!-- paragraph -->
```{r}
errorPlotNew+facet_grid(facet ~ n.folds, scales="free")
```
<!-- paragraph -->
Le code ci-dessous crée une visualisation interactive à l’aide du nouveau graphique de la courbe d’erreur.
<!-- paragraph -->
```{r ch10-vis-folds}
animint(
errorPlotNew+
theme_animint(width=325),
scatterPlot+
theme_animint(width=450, last_in_row=TRUE),
first=list(neighbors=7, n.folds=10))
```
<!-- paragraph -->
## Résumé du chapitre et exercices {#ch10-exercises}
<!-- paragraph -->
Nous avons montré comment ajouter deux fonctionnalités interactives à une visualisation des données des prédictions du modèle des K plus proches voisins.
<!-- comment -->
Nous avons commencé par une visualisation statique qui n’affiche que les prédictions des 7 plus proches voisins.
<!-- comment -->
Nous avons ensuite créé une visualisation interactive qui permet de sélectionner K, le nombre de voisins.
<!-- comment -->
Nous avons finalement proposé une autre visualisation, en ajoutant une facette qui permet de sélectionner le nombre de divsions dans la validation croisée.
<!-- paragraph -->
Exercices :
<!-- paragraph -->
- Faites en sorte que les taux d’erreur affichés dans le texte en bas à gauche du deuxième graphique soient masqués quand on clique sur les entrées de la légende pour Bayes, train et test.
<!-- comment -->
Conseil : vous pouvez soit utiliser un `geom_text()` avec `showSelected=c(selectorNameColumn="selectorValueColumn")` (comme expliqué dans le [chapitre 14](/ch14)) ou deux `geom_text` chacun avec un paramètre `showSelected` différent.
<!-- comment -->
- La colonne de probabilité (`probability`) du tableau de données `show.grid` est la probabilité prédite de la classe 1.
<!-- comment -->
Comment referiez-vous la visualisation pour montrer la probabilité prédite plutôt que la classe prédite à chaque point de la grille ?
<!-- comment -->
La difficulté principale est que la probabilité est une variable numérique, mais que `animint2` impose des échelles exclusivement continues ou discrètes (pas les deux).
<!-- comment -->
Vous pourriez utiliser une échelle continue pour `fill`, mais vous devrez alors utiliser une échelle différente pour montrer la variable de prédiction.
<!-- comment -->
- Ajoutez un nouveau graphique qui montre les tailles relatives des ensembles d’entraînement (`train`), de validation et de test.
<!-- comment -->
Assurez-vous que la taille tracée des ensembles de validation et d’entraînement change en fonction de la valeur sélectionnée de `n.folds`.
<!-- comment -->
- Jusqu’à présent, les graphiques de l’espace des variables ne montraient que les prédictions et les erreurs du modèle pour l’ensemble des données d’entrainement (`validation.fold==0`).
<!-- comment -->
Créez une visualisation qui inclut un nouveau graphique ou une nouvelle facette pour sélectionner `validation.fold`, et un graphique de l’espace des variables avec facettes (une facette pour l’ensemble de données d’entrainement, une facette pour l’ensemble de données de validation).
<!-- paragraph -->
Dans le [chapitre 11](/ch11), nous vous expliquerons comment visualiser le `Lasso`, un modèle d’apprentissage automatique.
<!-- paragraph -->